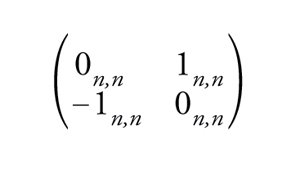Invarianti, Teoria degli

Invarianti, Teoria degli

La geometria proiettiva, e le geometrie non euclidee, ebbero un grande impatto sul pensiero algebrico e geometrico del secolo scorso. Le idee scaturite da questa teoria sono state riassunte da Felix Klein nel Programma di Erlangen e tendevano a presentare la geometria come lo studio delle proprietà di uno spazio invarianti per un gruppo di simmetrie (isometrie, affinità, proiettività). È in questo ambito che si inserisce la nascita e lo sviluppo della teoria degli invarianti, una singolare creazione degli algebristi del secolo scorso.

La teoria sviluppata in quel periodo è quasi esclusivamente ristretta allo studio delle forme algebriche, dette anche quantiche ossia polinomi omogenei di grado q in n+1 variabili. L'insieme delle forme di grado dato in un insieme di variabili è uno spazio vettoriale su cui opera il gruppo delle matrici invertibili (n+1)×(n+1) per sostituzione delle variabili. Se si considerano le n+1 variabili come coordinate proiettive, una forma algebrica rappresenta l'equazione di una (iper)-superficie nello spazio proiettivo a n dimensioni. Data una condizione geometrica su queste superfici (per es. la riducibilità, la singolarità, ecc.), è spesso possibile esprimerla algebricamente con un sistema di equazioni (o disequazioni) nei coefficienti della quantica. Se tale condizione ha un significato proiettivo intrinseco (indipendente dalle coordinate), il corrispondente sistema è invariante rispetto alle trasformazioni delle variabili. Sotto opportune ipotesi è possibile scegliere equazioni invarianti per poi determinare il luogo geometrico da esse definito.

L'esperienza di più di cento anni di ricerca ha mostrato che questi problemi sono spesso difficilissimi se non insolubili, invarianti assai semplici infatti possono avere interpretazioni geometriche del tutto oscure; d'altra parte vi sono numerosi esempi significativi in cui la teoria ha successo e rivela profonde simmetrie con le corrispondenti situazioni geometriche.

I maggiori successi della teoria classica si riferiscono al caso molto particolare delle forme binarie, ovvero le forme in due variabili. In linguaggio più moderno queste corrispon-dono alle rappresentazioni irriducibili del gruppo SU(2,ℂ) e il grado di una forma binaria al doppio dello spin nella terminologia della fisica quantistica. Osserviamo che seppure l'interpretazione geometrica di una forma binaria di grado q sulla retta proiettiva sia, come gruppo di q punti, estremamente semplice, la teoria si dimostra esttremamente complessa e ricca di problemi ancora aperti. Il culmine della teoria classica delle forme binarie è il teorema di finitezza di Gordan secondo il quale tutti gli invarianti delle forme binarie di grado dato si possono ottenere come polinomi in un numero finito fra di essi, e che porta allo sviluppo del cosiddetto metodo simbolico.

L'estensione della teoria a forme in più variabili è dovuta principalmente a Alfredo Capelli. Il suo maggiore contributo è nella direzione dei legami fra teoria degli invarianti e rappresentazioni dei gruppi, tema che verrà ripreso in varie forme da Hermann Weyl e Alfred Young. Negli ultimi anni dell'Ottocento David Hilbert in una serie di geniali lavori trasforma profondamente la teoria degli invarianti, sia nei metodi che nei contenuti. Uno dei principali risultati da lui ottenuti è l'estensione del teorema di finitezza di Gordan alle forme in un numero arbitrario di variabili. A questo scopo Hilbert prova una serie di teoremi generali sulle equazioni algebriche (quello della base, il Nullstellensatz, il teorema delle sizigie) e introduce nozioni fondamentali (sistemi di parametri, normalizzazione, punti instabili), creando i metodi moderni dell'algebra commutativa che avrebbero avuto poi un ruolo essenziale nella rifondazione della geometria algebrica. Della teoria simbolica egli utilizza l'operatore Ω di Cayley, che ha un ruolo importante anche nella teoria di Capelli.

Le idee di Hilbert furono inizialmente rifiutate per gli aspetti non algoritmici che esse contenevano ma, una volta che venne compresa, questa geniale opera ebbe un effetto dirompente sulla teoria degli invarianti: da una parte sembrò che Hilbert avesse risolto tutti i problemi della teoria stessa e dall'altra spostò vigorosamente la ricerca su nuovi argomenti. In questo modo, per un singolare scherzo del destino, intuizioni che dalla teoria degli invarianti dell'Ottocento avevano tratto la loro profonda motivazione segnano anche il suo atto di morte. La teoria delle forme binarie verrà sempre più dimenticata e solo negli ultimi trent'anni si cercherà di riscoprirne i metodi e i risultati.

Un momento di svolta

Nell'anno 1900 si svolgeva a Parigi il Congresso internazionale dei matematici e l'inizio del nuovo secolo conduceva a una riflessione sui possibili sviluppi della matematica stessa. L'appuntamento fu dominato dalla figura di Hilbert; tracciando idealmente una sintesi fra la matematica dell'Ottocento e alcuni percorsi della futura ricerca, egli propose ventitre problemi in campi diversi della matematica, dai fondamenti alla teoria dei numeri, fino all'algebra e all'analisi. Fra questi, almeno tre si possono considerare legati alla teoria degli invarianti: il quinto, il quattordicesimo e il diciassettesimo. Il più importante, ai fini della nostra trattazione, è il quattordicesimo problema.

Il quattordicesimo problema di Hilbert

A partire dalla soluzione data per le forme algebriche nel 1902, Hilbert formula una questione più generale: se l'intersezione fra un anello di polinomi e un sottocampo del suo campo delle frazioni sia sempre finitamente generata. Il problema ha avuto una lunga storia ma oggi sappiamo, grazie al lavoro condotto di Makoto Nagata nel 1959, che esistono gruppi per cui gli invarianti non sono finitamente generati e pertanto la risposta è negativa. D'altra parte una lunga serie di ricerche ha messo in evidenza una classe di casi notevoli in cui la risposta è positiva e in effetti il loro interesse va ben oltre quello del problema di Hilbert e si innesta nella teoria dei gruppi di Lie e dei gruppi algebrici.

Numerosi autori ‒ tra cui Ernst Fischer (1911) e Adolf Hurwitz (1933) ‒ hanno compreso come la prova di Hilbert sia connessa a un'idea fondamentale della teoria delle rappresentazioni: la possibilità di decomporre una rappresentazione in componenti irriducibili. Un gruppo (algebrico) per cui ogni rappresentazione (razionale) sia completamente riducibile si dice linearmente riduttivo e per esso vale il teorema di finitezza. Nel caso particolare di un gruppo finito in caratteristica zero vi è anche un approccio diretto ideato da Emmy Noether (1926), mentre in quello dei gruppi complessi la nozione di lineare riduttività è strettamente legata alla teoria dei gruppi di Lie compatti in virtù di un teorema generale di dualità di Mark G. Krein e Tadao Tannaka (1939). Questo teorema stabilisce infatti un'equivalenza categorica fra gruppi algebrici linearmente riduttivi e gruppi di Lie compatti, per i quali il metodo di decomposizione delle rappresentazioni è la cosiddetta integrazione invariante. Una tecnica, questa, utilizzata sistematicamente da Hurwitz e da Weyl (in alternativa all'uso del cosiddetto operatore Ω) e la cui formulazione in generale è dovuta ad Alfred Haar.

Riguardo poi ai gruppi connessi, e le loro rappresentazioni, si ha una precisa classificazione fondata sulla teoria di Wilhelm K. J. Killing, Cartan e Weyl sulle algebre di Lie semisemplici. Queste ricerche formano ora due importanti capitoli a cavallo tra l'algebra, la geometria e l'analisi: la teoria delle algebre di Lie semisemplici e la teoria dei gruppi di Lie compatti.

Negli ultimi cinquant'anni si è sviluppata la teoria generale dei gruppi algebrici ed è stata notata (specialmente a partire dai fondamentali lavori di Claude Chevalley sui gruppi finiti di tipo Lie) l'esistenza di una classe di gruppi ‒ detti riduttivi e definiti in ogni caratteristica ‒ per certi aspetti simili ai gruppi compatti connessi e di cui è stata data un'analoga classificazione. Un gruppo lineare algebrico si dice riduttivo se non possiede alcun sottogruppo normale non banale formato da soli elementi unipotenti (ossia con unico autovalore 1): in caratteristica 0 le nozioni di lineare riduttività e di riduttività coincidono, non così in caratteristica positiva. Eppure, nonostante le molte similarità fra gruppi compatti e gruppi riduttivi, nel caso di caratteristica positiva per questi ultimi la teoria delle rappresentazioni è molto complessa e in gran parte poco compresa anche se è stata data una soluzione positiva del problema di Hilbert.

Shigekazu Nagata ha introdotto la nozione di gruppo geometricamente riduttivo, mostrando che per tali gruppi vale il teorema di finitezza. David Mumford ha congetturato che le nozioni di riduttivo e geometricamente riduttivo siano equivalenti e questa importante congettura è stata provata nel 1974 da William Haboush con un elegante metodo della teoria delle rappresentazioni modulari. Per gruppi non riduttivi la teoria è molto lacunosa: a parte il controesempio di Nagata già menzionato, abbiamo un risultato speciale di Ronald Weitzenböck (1932) sul gruppo additivo in cui la teoria degli invarianti è ricondotta a quella del gruppo riduttivo SL(2,ℂ), un'idea che viene dalla classica teoria dei covarianti. Più in generale, Frank D. Grosshans (1973) introduce la classe dei gruppi osservabili, per cui si può ridurre la teoria degli invarianti a gruppi riduttivi. Nella maggior parte dei casi però le azioni dei gruppi non riduttivi sono molto misteriose e poco capite.

Il diciassettesimo problema di Hilbert

Il diciassettesimo problema di Hilbert chiede se una funzione razionale sempre positiva sia somma di quadrati di funzioni razionali. È legato alla teoria degli invarianti in quanto una delle idee di quest'ultima è determinare forme normali per funzioni che soddisfano particolari proprietà, forme tali cioè da mettere immediatamente in evidenza la proprietà in esame. Il problema è stato brillantemente risolto da Emil Artin e Otto Schreier nel 1927 sviluppando la teoria generale dei campi ordinati. Questi metodi sono tornati di attualità in tempi recenti grazie alla geometria algebrica reale.

Invarianti e rappresentazioni

A partire dalla fine del secolo scorso, per opera soprattutto di Georg F. Frobenius, la teoria delle rappresentazioni dei gruppi è stata al centro della ricerca matematica. Ci limiteremo agli aspetti legati alla teoria degli invarianti, non potendo certo neanche accennare, per esempio, alla monumentale moderna teoria delle rappresentazioni dei gruppi semisemplici o dei gruppi finiti; entrambe meriterebbero una trattazione a parte.

Nella teoria degli invarianti possiamo intravedere idee legate alle rappresentazioni fin dalle formule di Clebsch e Gordan sullo sviluppo delle forme binarie. Idee riprese da Capelli ed esposte nel classico libro Teoria delle forme algebriche (1902). Egli determina uno sviluppo delle forme in un numero qualunque di variabili vettoriali che, espresse nel linguaggio moderno, è equivalente a uno studio della decomposizione in irriducibili di tali spazi di forme. Le idee che portano da questo sviluppo di Capelli a una più moderna interpretazione passano attraverso i lavori di Alfred Young, Isaac Schur, Richard Brauer e Hermann Weyl. I risultati di queste ricerche si possono trovare esposte nel classico libro di quest'ultimo, The classical groups del 1939.

Negli anni venti, in maniera del tutto indipendente dagli sviluppi matematici, veniva creata a opera di Max Born, Louis de Broglie, Paul A. M. Dirac, Werner Heisenberg, Paul Jordan, Wolfgang Pauli e Erwin Schrödinger la meccanica quantistica, dimostratasi nel corso del Novecento uno strumento fondamentale per la costruzione di modelli matematici della fisica atomica e subatomica. A questa eccezionale stagione scientifica partecipò attivamente Weyl, che fu uno dei maggiori propugnatori dell'uso sistematico delle simmetrie nella formulazione di tali modelli.

Egli aveva contribuito in modo fondamentale, con la scoperta della formula dei caratteri, alla teoria generale sviluppata da Killing e Cartan. Avvertì quindi la necessità di presentare per i gruppi classici i concetti provenienti dagli approcci simbolici e algoritmici della teoria degli invarianti dell'Ottocento, concetti che erano alla base sia delle strutture algebriche utilizzate nei modelli della meccanica quantistica che della teoria generale delle algebre di Lie. L'idea guida è la seguente: i gruppi riduttivi sono facilmente costruiti a partire da quelli la cui algebra di Lie è semplice. Secondo la classificazione di Killing e Cartan, vi sono fra questi 5 gruppi eccezionali e 4 serie infinite, che corrispondono ai gruppi classici: la serie A_n del gruppo speciale lineare SL(n+1,ℂ)≡{X∈M_n+1,n+1(ℂ) tali che detX=1} (M_n+1,n+1(ℂ) indica lo spazio delle matrici (n+1)×(n+1) a coefficienti nel campo complesso ℂ e detX il determinante di X), le serie B_n e D_n dei gruppi speciali ortogonali e C_n dei gruppi simplettici. Ricordiamo che il gruppo ortogonale O(n,ℂ)≡{X∈M_n,n(ℂ) tali che XX^t=1} dove X^t indica la trasposta di X. Il gruppo speciale ortogonale è il sottogruppo formato dalle matrici con determinante uguale a 1. Il gruppo simplettico si definisce in modo analogo: Sp(n,ℂ)≡{X∈M_n,n(ℂ) tali che XJX^t=J} dove J è la matrice antisimmetrica 2n×2n, a blocchi di ordine n,

Ciascuno di questi gruppi ha una rappresentazione fondamentale V, quella in cui viene presentato sotto forma di matrici. Le idee classiche del metodo simbolico suggeriscono di determinare le altre rappresentazioni decomponendo le potenze tensoriali V^⊗m di quella fondamentale.

Il legame con la teoria degli invarianti è qui molto stretto. Per decomporre lo spazio dei tensori è infatti necessario determinare gli operatori lineari su tale spazio che commutano con l'azione del gruppo. D'altra parte lo spazio degli operatori lineari su V^⊗m può essere canonicamente identificato con lo spazio delle funzioni multilineari in m variabili in V e m variabili in V*, il duale di V. In questa identificazione, gli operatori che commutano con il gruppo corrispondono agli invarianti. Questa strategia, già presente in modo embrionale nell'opera di Capelli, è sfruttata sistematicamente da Schur per il gruppo lineare e poi da Brauer e Weyl per gli altri gruppi classici. La determinazione di generatori delle funzioni invarianti in m variabili in V e m variabili in V* viene detta da Weyl primo teorema fondamentale, e analogamente la determinazione di una base di relazioni fra tali generatori è detta secondo teorema fondamentale.

Il gruppo speciale lineare

Si considera lo spazio M_n,m(ℂ) delle matrici n×m su cui agisce SL(n,ℂ) per moltiplicazione a sinistra. Gli m!/n!(m−n)! determinanti dei minori di ordine n sono funzioni invarianti; assai più difficile (come sempre in teoria degli invarianti) è provare che tali invarianti generano l'intera algebra degli invarianti (primo teorema fondamentale). Il secondo teorema fondamentale esibisce esplicitamente delle relazioni quadratiche fra tali determinanti che generano l'ideale delle relazioni e generalizzano la classica quadrica di Klein.

Il gruppo generale lineare

Una matrice X∈GL(n,ℂ) opera su una coppia (A,B)∈M_p,n(ℂ)×M_n,m(ℂ) di matrici secondo la legge X(A,B)≡(AX⁻¹,XB); le pm coordinate della matrice prodotto AB sono invarianti e il primo teorema fondamentale afferma che esse generano l'algebra degli invarianti. Il secondo teorema fondamentale in questo caso afferma che le relazioni ovvie, ossia i determinanti dei minori di ordine n+1 il cui annullamento esprime il fatto che la matrice prodotto ha rango minore o uguale a n, generano l'ideale delle relazioni.

Il gruppo ortogonale O(n,ℂ) agisce invece sulle matrici A∈M_n,m(ℂ) per moltiplicazione a sinistra. Le m(m+1)/2 coordinate distinte della matrice simmetrica prodotto A^tA∈M_n,m(ℂ) sono generatori degli invarianti e i determinanti dei minori di ordine n+1 generano l'ideale delle relazioni.

Per quanto riguarda il gruppo simplettico Sp(n,ℂ), esso agisce per moltiplicazione a sinistra sulle matrici A∈M_n,m(ℂ). Le m(m−1)/2 coordinate distinte della matrice antisimmetrica prodotto A^tJA sono generatori degli invarianti e gli pfaffiani dei minori principali di ordine 2n+2 generano le relazioni.

Questi teoremi hanno un'interpretazione nella teoria delle rappresentazioni. Sia V uno spazio vettoriale di dimensione n sul campo complesso ℂ, allora l'algebra degli operatori su V^⊗m che commutano con il gruppo lineare GL(n,ℂ) di V è generata dal gruppo simmetrico S_m (primo teorema). Inoltre l'azione dell'algebra del gruppo simmetrico ha un nucleo, se m>n, generato dall'antisimmetrizzatore su n+1 elementi. Per i gruppi O(n,ℂ) e Sp(n,ℂ) la situazione è più complessa, nel centralizzatore vi sono altri operatori che provengono da opportune contrazioni dei tensori. È comunque possibile utilizzare la teoria restringendo la rappresentazione ai cosiddetti tensori a traccia nulla e Weyl segue questo metodo per determinare le rappresentazioni irriducibili dei gruppi classici e i loro caratteri.

L'utilità della determinazione del centralizzante di un'azione di un gruppo viene dalla teoria generale delle algebre semisemplici, sviluppata fra la fine dell'Ottocento e la metà degli anni Venti da Heinrich Maschke, William S. Burnside, Frobenius, Schur, Brauer, Weyl e in special modo da Joseph H.M. Wedderburn. Un'algebra S di operatori su uno spazio vettoriale W di dimensione finita si dice semisemplice se lo spazio W si decompone in somma di sottospazi irriducibili per l'algebra data. Il teorema di struttura di Wedderburn (1908) implica che l'algebra S è isomorfa alla somma diretta di algebre semplici S_i, ciascuna isomorfa a un'algebra di matrici M_ki,ki(ℂ). Ogni algebra M_k,k(ℂ) ha un'unica rappresentazione irriducibile, lo spazio dei vettori di dimensione k, e dunque lo spazio W è isomorfo come rappresentazione di S alla somma diretta degli spazi V_ki, ciascuno con una molteplicità p_i. Conseguenza è il fatto che l'algebra centralizzante S^t di S è ancora semisemplice e isomorfa alla somma diretta delle algebre M_pi,pi(ℂ), mentre rispetto a tale algebra W si decompone in modo tale che la rappresentazione irriducibile di M_pi,pi(ℂ) compare con molteplicità k_i. Vi è quindi una corrispondenza biunivoca fra le rappresentazioni irriducibili di S e quelle di S^t che compaiono in W, in cui dimensione e molteplicità vengono scambiate.

Da questo punto di vista la teoria delle rappresentazioni dei gruppi classici viene collegata in modo assai stretto con quella del gruppo simmetrico. La teoria del gruppo simmetrico inizia con il calcolo dei caratteri di Frobenius e culmina con i lavori di Young su simmetrizzatori e tabelle standard (1900).

Il gruppo simmetrico

I lavori di Young furono in gran parte motivati dal desiderio di dare una veste formale al metodo simbolico delle forme binarie. Dalla teoria di Frobenius sappiamo che le rappresentazioni irriducibili di un gruppo finito sono tante quante le sue classi coniugate. Per il gruppo simmetrico S_m la classe coniugata di una permutazione è determinata dalla lunghezza dei cicli in cui si decompone e pertanto le classi coniugate sono tante quante le partizioni di m. Data allora una partizione di m, si costruisce un diagramma con le righe formate da tante caselle quanti sono i numeri della partizione e riempiendo con i numeri da 1 ad m le caselle si ottengono due partizioni dell'insieme di tali numeri, quella data dalle righe e quella data dalle colonne. Da queste si costruiscono due sottogruppi del gruppo simmetrico, il gruppo H che preserva le righe e il gruppo K che preserva le colonne. Si formano poi le somme S≡∑_σ∈Hσ (il simmetrizzatore sulle righe) e A≡∑_σ∈Hε_σσ (l'antisimmetrizzatore sulle colonne), dove ε_σ è il segno della permutazione. Il prodotto P≡AS gode della proprietà di essere quasi idempotente (P²=cP con c una costante non nulla) e quindi si può definire c⁻¹P: è questo il codiddetto simmetrizzatore di Young. Questo genera nell'algebra del gruppo una rappresentazione irriducibile associata alla partizione data e, applicato allo spazio dei tensori V^⊗m, una corrispondente rappresentazione irriducibile del gruppo lineare di V.

Un altro contributo di Young è la teoria delle tabelle standard. Una tale tabella si ottiene riempiendo il diagramma con i numeri da 1 a m in modo tale che leggendo le righe da sinistra verso destra e le colonne dal basso verso l'alto i numeri risultino crescenti. Young prova che tali tabelle indicizzano naturalmente una base della corrispondente rappresentazione del gruppo simmetrico. Una teoria analoga, in cui si ammette di ripetere gli indici sulle righe, si ha per le rappresentazioni del gruppo lineare.

Interpretazione geometrica

La teoria degli invarianti è strettamente collegata alla geometria delle orbite. Il punto di vista geometrico è però quasi assente nella trattazione di Weyl, lo ritroviamo solo nei lavori di William D. Hodge e Jun-Ichi Igusa. Da questi autori è trattato in particolare il caso del gruppo speciale lineare. Infatti, seguendo le idee di Hermann Grassmann e Julius Plücker, i determinanti dei minori di ordine n di una matrice n×m di rango n si possono pensare come coordinate proiettive (le coordinate plückeriane) del sottospazio dello spazio a m dimensioni generato dalle righe. In questo modo l'insieme di tali sottospazi appare come una varietà proiettiva, la grassmanniana. Lo studio di questa varietà ha una lunga storia, che parte dalle idee della geometria numerativa di Hermann C. Schubert (1878) e di Francesco Severi e Wei-Liang Chow sulle coordinate proiettive da assegnare a una varietà algebrica, per arrivare a quelle topologiche di Charles Ehresman e su fibrati vettoriali e classi caratteristiche di Shing-Shen Chern.

Il legame con la teoria degli invarianti appare in vari modi, prima di tutto con la seguente osservazione di Severi: l'algebra generata dalle coordinate plückeriane è un dominio a fattorizzazione unica (essendo l'algebra degli invarianti di un gruppo connesso). Questo permette di definire la forma di Chow di una varietà W di dimensione k nello spazio proiettivo di dimensione n come equazione dell'ipersuperficie dei sottospazi di dimensione n−k−1 che incontrano W.

Il secondo collegamento è nelle idee di Hodge che, studiando la formula di postulazione per la grassmanniana (ovvero le dimensioni delle componenti omogenee dell'algebra generata dalle coordinate plückeriane), mostra come la teoria di Young sulle tabelle standard abbia una naturale interpretazione nel linguaggio delle celle di Schubert. I teoremi sugli altri gruppi classici hanno anche essi interpretazioni geometriche per lo studio delle cosidette varietà determinantali.

Invarianti e coomologia

Vi è un evidente e preciso legame fra invarianza per un gruppo continuo e connesso e omotopia. Questo fatto ha molte applicazioni importanti per lo studio della coomologia: ne menzioneremo solamente due.

Prima di tutto la coomologia degli spazi simmetrici compatti G/H secondo Cartan (1929) si ottiene considerando l'azione del gruppo H sull'algebra esterna costruita sullo spazio cotangente nella classe di 1. I calcoli espliciti che se ne deducono sono collegati ai teoremi classici e allo studio degli invarianti della rappresentazione aggiunta.

Il secondo esempio è più recente e riguarda la coomologia delle matrici infinite su un anello commutativo pensate come algebra di Lie. In questo caso un teorema di Boris L. Tsygan da un lato e Jean-Louis Loday e Daniel Quillen dall'altro permette di ridurre tale coomologia alla coomologia ciclica introdotta da Alain Connes (1982). La riduzione utilizza in modo essenziale la teoria della commutazione fra gruppo simmetrico e gruppo lineare sugli spazi tensoriali. Un teorema simile vale anche per le algebre di Lie dei gruppi classici che sono legate alla coomologia diedrale di Boris L. Feygin e Tsygan nonché di Loday-Procesi.

Gli sviluppi recenti

La teoria classica si restringeva alla caratteristica zero, ma tale restrizione è stata rimossa grazie ai lavori di Igusa prima (1946), di Peter Doubilet, Gian Carlo Rota e Joel A. Stein (1974) poi, e infine di Corrado De Concini e Procesi (1973).

Nel 1978 Alain Lascoux ha scoperto un'esplicita formulazione dell'n-esimo teorema fondamentale, ovvero una descrizione delle sizigie. Questo lavoro è stato chiarificato ed esteso da Tadeusz Jozefiak, Piotr Pragacz, Jerzy Weyman. La teoria del gruppo simmetrico e del gruppo lineare è stata estesa in vari modi: la corrispondenza di Gilbert de Beauregard Robinson e Craige Schensted (1938) fra parole e tabelle standard, la regola di Dudley E. Littlewood e Archibald R. Richardson (1934) sulla moltiplicazione dei caratteri del gruppo lineare, la presentazione di Wilhelm Specht della teoria di Young (1935), la teoria del monoide plactico di Marcel-Paul Schützenberger (1976) che dà una veste formale particolarmente efficace ai due risultati appena menzionati.

Per la rappresentazione aggiunta di un'algebra di Lie semisemplice la teoria degli invarianti è particolarmente precisa: sappiamo (grazie a Chevalley) che gli invarianti sono isomorfi agli invarianti del gruppo di Weyl agente sulla sottoalgebra di Cartan. Questa rappresentazione è data da un gruppo di riflessioni e per tali gruppi Chevalley stesso mostra (1955) che gli invarianti sono un'algebra di polinomi i cui gradi sono noti. Seguendo le idee di Harish-Chandra (che in parte sono già in Capelli), la struttura di questi invarianti determina il centro dell'algebra inviluppante e i caratteri sulle rappresentazioni irriducibili. Infine la teoria di Hodge sulle tabelle standard ha avuto una ampia estensione a opera della scuola di Conjeeveram S. Seshadri, che ha stabilito una teoria analoga per i gruppi semisemplici e le loro corrispondenti celle di Schubert-Bruhat.

Invarianti e orbite

Nei lavori di Hilbert vi è già uno studio approfondito del seguente problema: data un'azione di un gruppo algebrico G su una varietà affine V con anello di coordinate A tale che l'algebra A^G degli invarianti sia finitamente generata, essa può essere considerata l'algebra delle coordinate di una varietà algebrica V//G. L'inclusione A^G⊂A induce un morfismo di varietà π: V→V//G. Il morfismo è costante sulle orbite ed è interessante determinare il legame preciso fra punti di V//G e le G-orbite in V.

La teoria è stata sviluppata quasi esclusivamente nel caso dei gruppi riduttivi. Il morfismo π è suriettivo e ogni sua fibra contiene un'unica orbita chiusa: si può pertanto dire che V//G parametrizza le orbite chiuse di G in V. Nel caso in cui si voglia studiare l'azione di G su una varietà proiettiva, l'anello A deve essere considerato come dato da coordinate omogenee e analogamente gli invarianti vanno pensati come coordinate omogenee. Per avere un punto è necessario che non tutte le coordinate siano nulle e quindi determinare a priori per quali elementi di V tutti gli invarianti sono nulli. Tali elementi sono detti instabili. Nel caso di una rappresentazione lineare abbiamo un potente criterio dovuto a Hilbert e Mumford: un vettore è instabile se e solo se esiste un sottogruppo a un parametro λ(t) in G tale che lim_t→0λ(t)(v)=0. Mumford utilizza sistematicamente queste idee per costruire varietà di moduli di curve, superfici, fibrati vettoriali.

Il teorema delle slice étale di Domingo Luna (1972) permette di studiare la varietà quoziente nell'intorno di un suo punto P. L'orbita chiusa nella fibra di P ha come stabilizzatore un gruppo riduttivo, come mostrato da Yozo Matsushima. Si considera l'azione di tale gruppo sullo spazio normale all'orbita e Luna prova che il quoziente di questa azione è analiticamente isomorfo alla varietà V//G nell'intorno di P.

In un'altra direzione, George Kempf (1978) studia i sottogruppi ad un parametro che destabilizzano un punto instabile e ne trova uno ottimale. Questo teorema è stato sfruttato per esempio da Frances C. Kirwan (1982) per studiare la topologia delle varietà quozienti. Applicazioni della teoria degli invarianti sono date nei lavori di Hans-peter Kraft e Procesi (1979) sulle singolarità delle clas-si coniugate. In essi si utilizzano i teoremi fondamentali dei gruppi classici per presentare le chiusure di tali clas-si come quozienti di opportune varietà a intersezionecompleta.

Problemi di razionalità

Consideriamo ora il problema di determinare se ogni invariante si possa esprimere in modo unico come funzione razionale di invarianti indipendenti; se ciò avviene si dice che il campo è razionale. Una motivazione classica è il problema di Luroth, ovvero se un campo contenuto in un campo razionale sia anche esso razionale. Tale problema ha avuto recentemente una risposta negativa da parte di Herbert Clemens e Phillip A. Griffiths e da Michael Artin e Mumford (1972). Una motivazione di natura aritmetica viene dalla domanda, tuttora senza risposta, se ogni gruppo finito sia il gruppo di Galois di un'estensione dei razionali. Seguendo una strategia di Hilbert, si ha una risposta positiva a tale quesito se si trova un'azione di G su un campo di funzioni razionali a coefficienti razionali e tale che il campo degli invarianti sia puramente trascendente sui razionali stessi. Per esempio, se G permuta le variabili.

Negli anni Sessanta Richard Swan ha trovato un controesempio a questo problema nel caso abeliano, David Saltman nel caso complesso. In questa direzione possiamo menzionare anche i lavori di Shizuo Endo e Takehiko Miyata da un lato e Fedor A. Bogomolov dall'altro (1984). Il solo caso trattato in generale è quello delle rappresentazioni del gruppo SU(2,ℂ), che danno sempre luogo ad invarianti razionali.

Il teorema di Melvin Hochster e Paul Roberts (1974) dà informazioni nuove anche nel caso classico delle forme binarie. Gli autori provano che l'algebra degli invarianti (di un'azione lineare di un gruppo complesso riduttivo) gode della proprietà di Cohen-Macaulay: esistono due serie di invarianti u₁,…,u_n e v₁,…,v_m tali che ogni altro invariante si esprime in modo unico come combinazione lineare degli invarianti v_i a coefficienti polinomi negli invarianti u_i. Questo teorema ha avuto una utile estensione da Jean-François Boutot, il quale ha provato che le singolarità razionali si preservano per passaggio al quoziente.

Invarianti e algebra non commutativa

I teoremi fondamentali possono essere interpretati nel linguaggio degli invarianti di matrici. Dato lo spazio delle m-uple di matrici rispetto all'azione di coniugazione, gli invarianti sono generati da tutte le tracce dei monomi nelle matrici date. Il secondo teorema fondamentale afferma che tutte le relazioni fra tali invarianti si possono dedurre dal teorema di Cayley-Hamilton. Tali invarianti sono parametri per classi di isomorfismo di rappresentazioni e si utilizzano per lo studio di alcune interessanti algebre non commutative.

Rappresentazioni speciali

Una lunga serie di lavori classificano le rappresentazioni per cui gli invarianti o le orbite hanno proprietà speciali: per esempio, gli invarianti potrebbero essere un'anello di polinomi o le fibre del morfismo quoziente equidimensionali, ecc. Queste ricerche di Victor G. Kac, Vladimir L. Popov ed Ernest B. Vinberg hanno messo in evidenza numerosi esempi per cui la teoria degli invarianti e delle orbite può essere sviluppata in modo completo. La classificazione è stata precisata da Gerald W. Schwarz e da O. Adamovich e Y. Golovina; punto chiave dell'analisi è una stima sul numero minimo di invarianti che generano. Nella stessa direzione si collocano i lavori sulle rappresentazioni dei quivers di Peter Gabriel, Israel M. Gelfand e V.A. Ponomarev (1970).

Invarianti reali

La teoria è particolarmente sviluppata per i gruppi compatti. Le idee principali sono dovute a Kempf e a Linda Ness (1979) e sono motivate dalle classiche formulazioni della teoria dei momenti nel formalismo hamiltoniano della meccanica analitica. Presa una rappresentazione V di un gruppo complesso G, un sottogruppo compatto massimale K di G e una metrica K invariante su V, essi provano che la lunghezza di un vettore, ristretta ad una G orbita, ha valori critici solo se l'orbita è chiusa. In questo caso si ha che i valori critici sono tutti minimi e che i punti critici formano una K orbita. Se ne deduce un legame fra teoria delle orbite di G e di K che permette per esempio di determinare esplicite disequazioni per gli invarianti di un gruppo compatto (che generalizzano le classiche disequazioni di Sylvester per i polinomi a radici reali) e di provare alcune congetture su analoghi del problema diciassettesimo di Hilbert per gli invarianti.

Bibliografia

Capelli 1902: Capelli, Alfredo, Lezioni sulla teoria delle forme algebriche, Napoli, Pellerano, 1902.

Dickson 1914: Dickson, Leonard E., Algebraic invariants, New York, Wiley, 1914.

Dieudonné, Carrell 1971: Dieudonné, Jean A. - Carrell, James B., Invariant theory, old and new, New York-London, Academic Press, 1971.

Fogarty 1969: Fogarty, John, Invariant theory, New York, Benjamin, 1969.

Grace, Young 1903: Grace, John H. - Young, Alfred, Algebra of invariants, Cambridge, Cambridge University Press, 1903.

Gurevich 1964: Gurevich, Grigorii B., Foundations of the theory of algebraic invariants, Groningen, Noordhoff, 1964.

Hermann 1978: Hilbert's invariant theory papers, edited by Robert Hermann, Brookline (Mass.), Math Sci Press, 1978.

Kraft 1984: Kraft, Hanspeter, Geometrische Methoden in der Invariantentheorie, Braunschweig, Vieweg, 1984.

Kraft 1989: Algebraic transformation groups and invariant theory, edited by Hanspeter Kraft, Peter Slodowy, Tony A. Springer, Basel, Birkäuser, 1989.

Littlewood 1940: Littlewood, Dudley E., The theory of group characters and matrix representations of groups, New York-Oxford, Clarendon, 1940.

Meyer 1892: Meyer, Wilhelm F., Invariantentheorie. Enzyklopädie der mathematischen Wissenschaften, Leipzig, Teubner, 1892.

Mumford, Fogarty 1982: Mumford, David - Fogarty, John, Geometric invariant theory, 2. ed., Berlin-New York, Springer, 1982.

Murnaghan 1938: Murnaghan, Francis D., The theory of group representations, Baltimore, Johns Hopkins University Press, 1938.

Procesi 1982: Procesi, Claudio, A primer in invariant theory, Waltham (Mass.), University of Brandeis, 1982.

Schur 1968: Schur, Issai, Vorlesüngen über Invariantentheorie, edited by Helmut Grunsky, Berlin, Springer, 1968.

Springer 1977: Springer, Tony A., Invariant theory, Berlin-New York, Springer, 1977.

Weitzenböck 1923: Weitzenböck, Roland, Invariantentheorie, Groningen, Noordhoff, 1923.

Weyl 1939: Weyl, Hermann, The classical groups. Their invariants and representations, Princeton (N.J.), Princeton University Press, 1939.