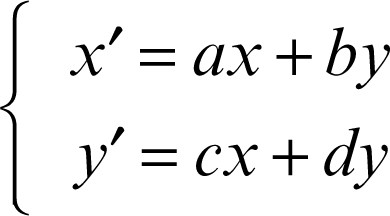Sistema differenziale, stabilita di un

sistema differenziale, stabilita di un

sistema differenziale, stabilità di un proprietà di un sistema dinamico di equazioni differenziali corrispondente alla nozione intuitiva di non avere una evoluzione esplosiva o imprevedibile, ma di tendere, al crescere del tempo, a un regime stazionario o periodico. Si descrivono qui di seguito queste nozioni con riferimento al caso bidimensionale, nel quale è possibile disegnare sul piano (x, y) delle due componenti del vettore incognito le traiettorie delle soluzioni (ritratto di fase del sistema).

Nel caso lineare, un sistema differenziale omogeneo del secondo ordine ha la forma

Le sue soluzioni stazionarie (cioè costanti nel tempo, e quindi corrispondenti a x′ = y′ = 0) sono le soluzioni di un sistema algebrico lineare e, nel caso non singolare (ad − bc ≠ 0), si riducono alla sola origine. La discussione del ritratto di fase dipende dalla natura della matrice dei coefficienti e, in particolare, dai suoi autovalori λ₁ e λ₂ e conduce alla seguente casistica:

1) Autovalori reali distinti. Due traiettorie sono le rette passanti per l’origine e aventi la direzione degli autovettori; le altre sono curve tangenti nell’origine alla retta corrispondente all’autovalore di modulo minimo. In dettaglio:

a) se entrambi gli autovalori sono negativi, tutte le traiettorie convergono verso l’origine, che è un nodo proprio stabile;

b) se entrambi gli autovalori sono positivi, tutte le traiettorie divergono dall’origine, che è un nodo proprio instabile;

c) se gli autovalori hanno segni opposti, le uniche traiettorie passanti per l’origine sono le rette, mentre le altre hanno quelle rette come asintoti: si dice allora che l’origine è una → sella.

2) Autovalori reali coincidenti:

a) se la matrice è diagonalizzabile, tutte le soluzioni sono rette passanti per l’origine, stabile se λ < 0, instabile se λ > 0;

b) se la matrice non è diagonalizzabile, essa è equivalente a un blocco di Jordan (→ Jordan, matrice di); all’autovalore λ corrisponde un solo autovettore u₁ e un autovettore generalizzato u₂ soluzione del sistema [A − λI₂]u₂ = u₁.

L’integrale generale è (C₁t + C₂)u₁e^λt + C₁u₂e^λt. Tutte le traiettorie tendono asintoticamente all’origine in direzione tangente a quella dell’autovettore u₁, per t → +∞ se λ < 0 (nodo improprio o nodo a una tangente stabile), per t → −∞ se λ > 0 (nodo improprio instabile).

3) Autovalori complessi coniugati λ = α ± i β. Se α ≠ 0, le traiettorie sono spirali che tendono all’origine per t → +∞ se α < 0 (fuoco stabile) o se ne dipartono per t → −∞ se α > 0 (fuoco instabile). Se α = 0 le traiettorie sono ellissi con centro nell’origine, che appunto si descrive come centro per il sistema. Un centro è un punto stabile, ma non asintoticamente stabile (le traiettorie non tendono a esso per t → +∞).

La teoria si generalizza in m dimensioni, il segno negativo della parte reale degli autovalori essendo sempre la condizione primaria per la stabilità dell’equilibrio nell’origine.

Nel caso non lineare, definito dal sistema

o, sinteticamente, X′ = F(X), si possono avere più punti di equilibrio, o punti stazionari, corrispondenti alle soluzioni del sistema F(X) = 0. Un punto stazionario P si dice localmente stabile se per ogni ε > 0 esiste δ > 0 tale che, per ogni soluzione X(t) tale che |X(0) − P| < δ, risulti |X(t) − P| < ε per ogni t ≥ 0. In caso contrario P si dice instabile. Un punto stazionario P localmente stabile si dice localmente asintoticamente stabile se per tutti i dati iniziali che distano meno di un opportuno ρ > 0 da P la soluzione X(t) tende a P per t → +∞.

Si chiama bacino di attrazione di un punto stazionario P l’insieme B(P) di tutti i punti Q tali che le traiettorie spiccate da Q tendano a P per t → +∞ (→ attrattore).

Dualmente, dato un punto Q, la traiettoria X(t) uscente da Q, cioè con X(0) = Q, può non avere limite; tuttavia è possibile che essa transiti sempre più vicina a un punto P, nel senso che esiste una successione di istanti {t_n} → +∞ tale che |X(t_n) − P| → 0, per n → +∞. L’insieme di tali punti P costituisce il cosiddetto insieme ω-limite di Q, e si denota con ω(Q). Un ciclo ω-limite del sistema è un’orbita chiusa γ ⊂ ω(Q) corrispondente a un dato iniziale Q ∉ γ. Analogamente si parla di insieme α-limite α(Q) o di ciclo α-limite se t_n → −∞.

Infine, si definiscono due tipi di orbite che tendono a qualche punto di equilibrio:

• le orbite omocline X(t), che sono caratterizzate dal fatto che tendono allo stesso punto stazionario P sia per t → −∞ sia per t → +∞;

• le orbite eterocline X(t), che tendono a un punto di equilibrio Q per t → −∞ e a un diverso punto di equilibrio P per t → +∞.

La stabilità di un punto P per un sistema si studia principalmente con due metodi:

a) per linearizzazione, sostituendo al sistema X′ = F(X) il sistema linearizzato X′ = JX, in cui J è la matrice jacobiana di F nel punto (che si può sempre pensare traslato nell’origine, usando come incognita il vettore X − P). In particolare, se tutti gli autovalori di J hanno parte reale negativa, il punto P è localmente asintoticamente stabile;

b) mediante le cosiddette funzioni di Ljapunov. Queste sono funzioni V(X), definite in un intorno Ω dell’origine O, che godono delle seguenti proprietà: V(O) = 0, V(X) > 0 per X ≠ O e per ogni soluzione globale X(t) del sistema risulta dV(X(t))/dt ≤ 0 per t > 0. V si dice funzione di Ljapunov stretta se l’ultima disuguaglianza vale col segno di < stretto. Si mostra che se esiste una funzione di Ljapunov, l’origine è punto di equilibrio stabile; se esiste una funzione di Ljapunov stretta, l’origine è punto di equilibrio asintoticamente stabile.

Una volta studiati localmente i singoli punti di equilibrio, si cerca una descrizione dell’intero insieme delle traiettorie individuando la possibilità di esistenza di orbite omocline o eterocline, di cicli limite, di orbite periodiche o di altre proprietà qualitative delle traiettorie.

Tipica è anche l’insorgenza del cosiddetto → caos deterministico, corrispondente a un comportamento nel quale una piccola variazione dei dati iniziali conduce a soluzioni drasticamente differenti per t crescente, e quindi a una pratica impossibilità di conoscere l’andamento futuro del sistema. Questo fenomeno fu scoperto nel 1963 da Edward N. Lorenz nello studio di un modello meteorologico semplificato e rende ragione dell’impossibilità teorica di ottenere previsioni precise a medio e lungo termine.

Nel caso in cui il sistema dipenda da un parametro, si possono individuare i valori di questo che separano un tipo di comportamento da un altro (→ biforcazione).