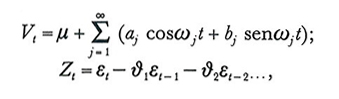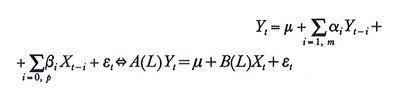Serie storiche, analisi delle

Serie storiche, analisi delle

sommario: 1. Finalità. 2. Nota storica. 3. I modelli temporali classici per componenti: a) descrizione dei modelli; b) separazione delle componenti e analisi. 4. Modelli probabilistici: a) processi stocastici stazionari e non stazionari; b) analisi temporale dei processi stazionari: i processi ARMA; c) analisi spettrale dei processi stazionari. 5. Serie storiche non stazionarie e relazioni tra serie storiche. □ Bibliografia.

1. Finalità

Una serie storica è un insieme finito cronologicamente ordinato di osservazioni x_₁, x_₂, x_₃,..., xT relative a un carattere X, generalmente equidistanti, ove l'indice indica il tempo, che è spesso un numero intero (serie storica discreta) o talora un numero reale variabile in un intervallo (serie storica continua); l'ordine dei dati è la caratteristica peculiare delle serie storiche. Esse possono essere posizionali (se esprimono le misure di un fenomeno a dati istanti, come l'ammontare della popolazione o dell'occupazione) e di flusso (se forniscono la misura del fenomeno con riferimento a intervalli di tempo, come le serie storiche mensili dei matrimoni e delle nascite o la serie storica trimestrale del reddito prodotto). L'analisi delle serie storiche è l'insieme delle procedure che permettono di studiare l'evolversi dei fenomeni al trascorrere del tempo, sia nell'ambito naturalistico sia in quello dei sistemi economici e sociali; essa può essere: 1) univariata, se mira a descrivere, interpretare, prevedere e controllare una singola serie storica nella sua dinamica temporale, tentando di spiegare il meccanismo che la genera e di prevederne il comportamento nel suo sviluppo futuro; 2) multivariata, se mira alla ricerca di connessioni e relazioni fra più serie storiche. Le finalità che l'analisi persegue si compendiano nelle seguenti: a) descrittive, consistenti nel presentare i dati mediante grafici; nell'esplorarli con strumenti statistici e misure sintetiche atte a cogliere le caratteristiche della serie storica, fra cui la stazionarietà, la presenza di una tendenza, i segnali di un ciclo, l'esistenza di effetti stagionali, l'identificazione di irregolarità e disomogeneità (dati mancanti o dati abnormi non consistenti con gli altri e dovuti ad annate sfavorevoli, calamità naturali, scioperi, guerre, effetti di calendario, errori di rilevazione), nonché a individuare punti di discontinuità (cioè improvvisi cambiamenti di livello, che spesso rivelano modificazioni determinatesi nella struttura interna della serie storica anche per effetto di interventi di politica economica o sociale: in tal caso, se possibile, è opportuno suddividerla in segmenti omogenei); nell'effettuare aggiustamenti, eliminazioni, sostituzioni e trasformazioni preliminari dei dati: di largo uso sono i tassi di variazione rispetto al periodo precedente o rispetto allo stesso periodo dell'anno precedente, nonché le trasformazioni logaritmiche che attenuano la variabilità dei dati quando è molto elevata, seguite spesso dall'applicazione dell'operatore ∇ calcolando le differenze tra un dato e il precedente, che esprimono valori approssimati dei saggi relativi di variazione del fenomeno che la serie storica descrive; b) esplicative, il cui obiettivo è la ricerca del meccanismo che può aver dato origine all'insieme delle osservazioni - espresso da un modello ipotetico, generalmente matematico, capace di riprodurre i dati che compongono la serie storica come realizzazione del processo generatore - nonché la spiegazione degli eventuali nessi correlativi o causali fra più serie e la verifica di ipotesi; c) previsive, volte a gettare uno sguardo verso il futuro - a breve, medio o lungo termine - con l'ausilio di metodi oggettivi e soggettivi; lo scopo previsivo viene spesso privilegiato, ma esso non è né specifico né peculiare, essendo altrettanto importanti le finalità descrittive e interpretative, e specialmente l'identificazione del processo generatore della serie storica. Le previsioni vengono generalmente elaborate assumendo che i fattori che hanno manifestato rilevanza nell'evoluzione temporale passata agiscano e interagiscano anche per il futuro con le stesse modalità: si tratta quindi per lo più di proiezioni (estrapolazioni), i cui risultati vanno comunque configurati nella logica dell'incerto; peraltro, il loro grado di fiducia decresce rapidamente con l'allontanarsi dell'orizzonte temporale cui si riferiscono. Vere e proprie previsioni richiedono analisi approfondite (con la dovuta attenzione su effetti effimeri, cambiamenti temporanei, variazioni di direzione, modifiche della variabilità, ecc.) da collegare a eventi critici e a possibili cambiamenti strutturali nell'andamento della serie storica; d) di controllo di processi e sistemi che si evolvono nel tempo, finalità questa di minore importanza nelle scienze sociali.
L'analisi delle serie storiche viene svolta seguendo due principali approcci, concepiti rispettivamente nel dominio frequenziale e nel dominio temporale. Nel dominio frequenziale l'obiettivo è la scomposizione spettrale della serie storica nelle sue componenti periodiche fondamentali, ciascuna caratterizzata da un differente ammontare di varianza; in quello temporale i modelli vengono formulati in termini di tempo, di rapporti passato-presente, di memoria della serie, di autocovarianza e autocorrelazione tra i dati. I due approcci, pur ponendo quesiti diversi, sono matematicamente equivalenti, come dimostrato da Wiener e Khintchine (v. Gottman, 1981, cap. 16), essendo semplicemente metafore diverse per concepire e trattare i dati; la costruzione di un modello del processo generatore dei dati osservati può essere realizzata usando modelli frequenziali, modelli temporali e modelli integrati, e la risposta ai quesiti può ottenersi impiegando come strumenti di base la funzione di densità spettrale e la funzione di autocorrelazione.

2. Nota storica
Fin dal XIX secolo un notevole interesse fu incentrato sulle ricerche di periodicità nascoste (non riscontrabili all'ispezione grafica) in vari fenomeni naturali, e già nel Settecento Daniel Bernoulli aveva suggerito che un'ampia classe di funzioni potesse essere approssimata da una somma di funzioni goniometriche. La questione fu ripresa da Jean Baptiste Fourier - il quale dimostrò (1822) che ogni serie storica può essere approssimativamente rappresentata da una somma di seni e coseni - e sviluppata nel XIX secolo e nei primi decenni del XX. L'estrazione di oscillazioni periodiche dai dati osservati di una serie storica ha ricevuto un'attenzione crescente dalla fine dell'Ottocento; i primi ricercatori, seguendo Arthur Schuster, assumevano il modello xt = mt + zt, in cui mt è la componente sistematica oscillatoria (deterministica) e zt una variabile gaussiana di disturbo; impiegando l'analisi di Fourier, Schuster inventò e utilizzò largamente il periodogramma - grafico delle varianze associate alle frequenze delle diverse componenti - ottenuto come stima della funzione di densità spettrale, conferendo, nel contesto delle teorie preprobabilistiche, un chiaro significato alle frequenze delle componenti ondulatorie. L'argomento fu approfondito negli studi di J. Whittaker e P. Robinson (1924), in quelli dello stesso Schuster e di William Beveridge, e verso la metà degli anni quaranta nelle ricerche di Maurice Kendall e Maurice Bartlett: da tutti questi studi emersero vari difetti dello strumento, il cui uso poteva condurre a risultati fuorvianti. Il concetto di periodogramma fu generalizzato da Norbert Wiener nel corso del lento slittamento dalla visione deterministica a quella probabilistica delle serie storiche; in effetti, il periodogramma era riferito a valori fissi delle ampiezze e delle fasi, mentre le serie storiche - in particolare nell'ambito delle scienze sociali - sono quasi sempre caratterizzate da variazioni casuali di dette grandezze: l'assunzione deterministica non è realistica, e assai poche sono le serie prive al loro interno di elementi di disturbo. Nel corso degli anni venti Udni Yule dimostrò che periodo e ampiezza non sono costanti; tuttavia il concetto di periodogramma, alquanto modificato attraverso opportuni livellamenti, è usato ancor oggi nel dominio frequenziale come strumento dell'analisi spettrale, specialmente nello studio di serie storiche stazionarie (v. § 4c). Una teoria coerente dell'analisi statistica su osservazioni correlate nel tempo cominciò a prendere forma verso la metà degli anni venti con i contributi di Slutzky, Yule, Birkhoff, Wiener e Khintchine; via via si acquisì consapevolezza che molteplici problemi non potevano essere affrontati e risolti lungo le linee dei modelli classici, sostanzialmente deterministici, fino ad allora imperanti. Yule mostrò che una serie storica poteva essere meglio descritta come funzione dei suoi valori passati, e introdusse la nozione di modello autoregressivo, in cui xt è espressa da una funzione di se stessa calcolata in epoche precedenti, concetto esteso poi da Walker nei primi anni trenta. Khintchine mostrò che una serie storica poteva intendersi come realizzazione di un processo casuale di variabili aleatorie X_₁, X_₂,..., XT campionate a intervalli di tempo equidistanti: approccio perfezionato da Andrej Kolmogoroff, il quale negli stessi anni mostrò che esso corrisponde a una distribuzione di probabilità a T dimensioni, per cui sono applicabili la teoria probabilistica e la statistica. Verso la fine degli anni trenta Eugen Slutzky presentò il modello a medie mobili, in cui si assume che xt sia generata da una successione di variabili casuali indipendenti identicamente distribuite, e nel 1938 Herman Wold dimostrò la sua famosa formula di scomposizione di una qualsiasi serie stazionaria (v. § 4b), stabilendo un collegamento fra serie storiche e processi stocastici stazionari; infine, il teorema di Wiener e Khintchine facilitò la stima della funzione di densità spettrale utilizzando le usuali stime della funzione di autocovarianza, consentendo di passare in modo duale dal dominio temporale a quello frequenziale e viceversa, e affiancandone i relativi approcci. Tutto ciò aprì la strada verso la moderna analisi temporale delle serie storiche; la progressione storica delle ricerche indica lo stretto legame tra l'analisi temporale e i metodi frequenziali. Gli ultimi cinquant'anni testimoniano una crescita senza precedenti nell'area dell'analisi delle serie storiche, nonostante lo sviluppo dei metodi non sempre risponda alle reali esigenze degli studi nel campo delle scienze sociali, anche perché gli strumenti impiegati non possiedono caratteristiche generali che permettano di utilizzarli in problemi diversi. Peraltro, le potenziali applicazioni sono ancora in fase di consolidamento; paradossalmente, nell'area sociale sono stati poco impiegati metodi teoricamente validi, mentre le più semplici ma meno rigorose tecniche di decomposizione e di filtraggio hanno trovato una larga applicazione.

3. I modelli temporali classici per componenti
a) Descrizione dei modelli
Il principio su cui sono basati i modelli tradizionali di scomposizione delle serie storiche è ancorato all'ipotesi che la descrizione del comportamento di una serie storica nel campo sociale (specialmente nell'area economica) possa esprimersi mediante la sovrapposizione di varie componenti, prefissate ma non osservabili senza rimuovere gli effetti delle altre. La formulazione addittiva - in cui si ritiene che ogni componente si manifesti con un effetto autonomo - è del tipo: xt = mt + εt = (τt + ct + st) + εt; la componente mt esprime la parte deterministica o sistematica, articolata a sua volta nella tendenza o trend τt, nella componente ciclica ct e nell'eventuale componente stagionale st; εt è la componente accidentale o residuale connessa a variazioni di brevissimo periodo, che riassume errori e perturbazioni di ogni genere nonché tutti gli effetti non facilmente esplicitabili, dovuti a numerosi fattori che esercitano la loro influenza in misura e direzione variabili - con effetto medio complessivo generalmente trascurabile - i quali tendono a configurarla come variabile di tipo casuale. Essa congloba tuttavia anche variazioni di natura irregolare o episodica (effetti di eventi eccezionali, irregolarità di calendario, ecc.) che devono essere preliminarmente identificate, analizzate ed eventualmente eliminate o sostituite. La componente ciclica ct - concepita come deterministica con ampiezza e fase costanti - è attribuita a cause che tendono a imprimere al fenomeno un movimento oscillatorio intorno al trend, costituito da fluttuazioni ricorrenti ma non periodiche, susseguentisi a intervalli variabili e associabili a fattori naturali, demografici e politici, e specialmente ai movimenti di espansione e contrazione dei sistemi economico-sociali (oscillazioni congiunturali). La presenza del trend può essere rilevata dal valore dello spettro nell'origine (v. § 4c), mentre l'individuazione dei cicli regolari è facilitata dall'ispezione dei picchi dello spettro. Poiché in una serie storica osservata per periodi finiti non molto lunghi le componenti periodiche di bassa frequenza possono confondersi con la tendenza, spesso quest'ultima si considera immersa nelle ciclicità a bassa frequenza, facendo riferimento a un'unica componente trend-ciclo: in questa concettualizzazione la tendenza si configura statisticamente come una componente a bassa frequenza. Infine, la componente stagionale st esprime il comportamento della serie attribuibile all'avvicendarsi di fenomeni climatici e istituzionali (derivanti da leggi, abitudini, usanze, ecc.) comunque collegati con il ciclo annuale del calendario solare, i cui effetti si manifestano con un movimento oscillatorio secondo variazioni ricorrenti e periodiche - costanti o variabili - a intervalli di 12 mesi. La presenza di interazioni e correlazioni fra componenti può esprimersi con un modello moltiplicativo - riconducibile a quello addittivo mediante trasformazioni logaritmiche - o misto, a stagionalità costante o variabile.
Oggetto dell'approccio classico - il più tradizionale e il più orientato su procedure empiriche - è la valutazione e separazione delle componenti. Esso ebbe inizio agli albori di questo secolo al fine di eliminare o isolare il trend; in seguito, per le esigenze dell'analisi congiunturale si passò allo studio del ciclo, mentre la stagionalità cominciò a destare l'attenzione degli studiosi agli inizi del primo conflitto mondiale; al riguardo, F. Macauley introdusse il metodo dei rapporti di stagionalità, ancor oggi impiegato con molteplici varianti e perfezionamenti. La semplicità concettuale del modello si traduce in larga misura in automaticità delle procedure di analisi; esistono tuttavia vari procedimenti per la valutazione e scissione delle componenti, la cui scelta è connessa agli obiettivi perseguiti (eliminazione o isolamento del trend, determinazione di serie destagionalizzate, estrazione delle componenti deterministiche per lo studio delle proprietà del residuo, previsioni, ecc.). L'approccio classico si presta a numerose critiche (v. Piccolo e Vitale, 1981, p. 470), fra cui la presunzione di validità del modello per tutte le serie storiche, i procedimenti di filtraggio stabiliti a priori e la mancanza di ogni riferimento - salvo aspetti marginali - alla struttura probabilistica delle serie storiche, la cui scissione viene condotta con metodi uniformi qualunque sia il meccanismo casuale interno.

b) Separazione delle componenti e analisi
Per ricondursi alla sola componente residuale - che si suppone possa essere descritta da una variabile stazionaria in media - occorre valutare il trend (o il trend-ciclo) rimuovendo gli effetti delle oscillazioni di breve o medio termine; a tal fine una guida è l'impiego del covariogramma o del correlogramma e dello spettro, cioè dei grafici rispettivamente delle funzioni stimate di autocovarianza, di autocorrelazione e di densità spettrale (v. §§ 4a e 4c). Nelle serie storiche mensili o trimestrali il movimento tendenziale può essere messo in evidenza da medie annuali o calcolando le variazioni percentuali di un dato rispetto a quello del corrispondente periodo dell'anno precedente; per esso si ammette un comportamento regolare che consente di descriverlo mediante una funzione polinomiale del tempo di grado opportuno - i cui parametri vengono generalmente stimati con il metodo dei minimi quadrati - o anche mediante funzioni non lineari nei parametri (esponenziali, logaritmiche, e per andamenti sigmoidi la funzione di Gompertz o la logistica); per apprezzare le ciclicità le serie storiche vengono preliminarmente destagionalizzate rimuovendo la componente specifica. L'intero modello può anche essere parametrizzato e stimato mediante regressione; assumendo una formulazione addittiva, la componente trendciclo viene espressa da un polinomio in t e quella stagionale da una funzione periodica di periodo idoneo; la componente accidentale si assume a media nulla, varianza costante e covarianze nulle, mentre il metodo di stima è usualmente quello dei minimi quadrati, con il vincolo che la somma dei coefficienti stagionali sia nulla. Va osservato che il polinomio che rappresenta il trend-ciclo si considera valido per l'intero periodo, per cui il modello non prevede la possibilità di variazioni strutturali nel movimento tendenziale. Una variante prevista nei casi di stagionalità variabile consiste nell'assumere i coefficienti stagionali come funzioni - di solito lineari - del tempo. L'ipotesi che il trend possa descriversi con un polinomio a parametri costanti è però raramente realistica; il metodo di analisi e previsione proposto da Holt e Winters rappresenta un tentativo, orientato a scopi di previsione, di tener conto di variazioni nel trend, con parametri che si modificano nel tempo; esso rientra fra quelli basati su una diversa ponderazione delle osservazioni utilizzate, attribuendo un ruolo di maggiore rilevanza a quelle più recenti (v. Gambetta, 1991, cap. 4.3). La procedura, riconducibile al modello classico, è automatica e flessibile: la sua genesi è stata di tipo descrittivo, e solo in seguito se ne è dedotto il modello probabilistico di base.
Un'alternativa alle tecniche di regressione è la ricerca su base empirica di procedure che permettano un aggiornamento sistematico dei valori assunti dal trend a mano a mano che si dispone di nuove informazioni; si tratta del metodo della media (o somma) mobile, la cui descrizione è in gran parte riconducibile a formulazioni analitiche mediante polinomi mobili a coefficienti variabili. La scelta del tipo e della lunghezza della media mobile è generalmente soggettiva, e dipende dalla specifica serie e dai metodi disponibili, in modo che si conservi una delle componenti e si annullino approssimativamente le altre. Molto successo ha riscosso in passato, in particolare nell'ambito delle tavole di mortalità, la media mobile di Spencer a 15 e 21 elementi - capace di annullare stagionalità di periodo 4 o 5 e di rimuovere trend polinomiali fino a quelli cubici - e più recentemente le medie mobili di Henderson. Il metodo delle medie mobili si è aperto, in un contesto meno empirico, alle teorie e applicazioni del filtraggio lineare, cioè di trasformazioni lineari dei dati con coefficienti, non necessariamente simmetrici e a somma unitaria, che ne costituiscono il nucleo; la trasformata di Fourier del nucleo, denominata funzione di trasferimento o di trasferta, descrive il cambiamento intervenuto nel contenuto frequenziale e consente di ottenere la densità spettrale della serie storica filtrata. Le tecniche di filtraggio lineare, assai diffuse, riducono la variabilità, e nel dominio frequenziale eliminano o riducono le frequenze più alte e rapide; esse hanno acquisito importanza pratica specialmente con i contributi di R. Kalman (1960) che ne hanno favorito l'applicazione su larga scala con l'impiego del calcolatore. Può farsi rientrare nel filtraggio il cosiddetto livellamento esponenziale, introdotto intorno al 1960 nell'ambito della ricerca operativa e orientato verso la previsione; in esso si attribuisce un peso maggiore ai dati più recenti (v. Santamaria, 1981, cap. 5). Una forma particolare di filtraggio lineare assai diffusa è rappresentata dall'applicazione unica o ripetuta ai dati dell'operatore differenza ∇xt = xt - xt-₁. In relazione al grado, la differenziazione è equivalente all'eliminazione di un trend polinomiale; normalmente, le differenze del primo o del secondo ordine sono sufficienti a rimuovere trend di vario tipo. Peraltro, l'operatore è in parte interpretabile, poiché ∇ stima il saggio di variazione e ∇² la variazione del saggio di cambiamento (accelerazione). Generalmente la differenziazione è preferibile e appropriata quando sussiste un'elevata autocorrelazione positiva fra dati adiacenti, mentre la media mobile lo è quando l'autocorrelazione è negativa: entrambe tendono comunque ad annullarla. L'impiego di filtri lineari va effettuato con cautela, poiché tendono ad alterare, con sovrastime o sottostime a seconda della concavità, il contenuto frequenziale dei cicli della serie storica costituente l'input (effetto Slutzky-Yule) e a introdurre in conseguenza, nell'output risultante, comportamenti spuri prima non esistenti, attribuibili alle correlazioni seriali artificiali - e quindi alle periodicità apparenti - prodotte dal filtraggio.
L'eliminazione della componente stagionale può effettuarsi con differenziazioni del tipo ∇_₁₂ = xt - xt_-₁₂; assai più frequente è però l'applicazione del metodo - collaudato su migliaia di serie e per lunghi periodi - che determina il trend-ciclo operando con un filtro lineare simmetrico su dati mensili, con pesi che eliminano la stagionalità senza distorcere eccessivamente le altre componenti. Si tratta di un algoritmo con operatore media mobile di 12 termini centrata, fondato sull'esperienza empirica e notevolmente diffuso; la procedura su calcolatore, curata per decenni da Julius Shiskin nelle varie versioni, è nota come metodo X.11. Il programma relativo prevede numerose varianti e opzioni, impiegando tecniche e schemi sofisticati per rimpiazzare i valori perduti all'inizio e alla fine delle serie trattate, per identificare ed eliminare o sostituire gli outliers, per tener conto della diversa lunghezza dei mesi e del diverso numero di giornate lavorative; esso consente altresì l'uso di modelli moltiplicativi e addittivi, e la specificazione del tipo di media mobile che s'intende usare. Le componenti sono isolate una alla volta, determinandone una prima stima grezza che viene poi affinata ripetendo gran parte del processo di calcolo. La maggior parte delle regole ha carattere empirico; il programma è stato oggetto di molte critiche per la sua attitudine a distorcere le serie e le loro componenti e a eliminare solo i maggiori picchi di stagionalità. Procedure più valide sono basate su modelli ARIMA stagionali o sul filtraggio delle serie storiche attraverso l'analisi spettrale, che rimuove le frequenze senza alterare la forma-base dei dati.

4. Modelli probabilistici

a) Processi stocastici stazionari e non stazionari
Un modello di serie storica risulta da un insieme di assunzioni fatte circa il processo matematico che può aver generato la serie. L'idea fondamentale dei modelli probabilistici su serie storiche è di concepire una successione di informazioni x_₁, x_₂,..., xT come scaturente da osservazioni condotte su una famiglia {Xt} di variabili casuali X_₁, X_₂,..., XT, una per ogni valore di t, che nel loro insieme definiscono una parte finita di un processo stocastico; un processo stocastico discreto è costituito da una sequenza infinita di variabili casuali ordinate, mentre la serie storica ne è una realizzazione finita, costituita da valori - generalmente equidistanti - assunti da un insieme finito di variabili estratte dal processo. I problemi d'inferenza riguardano la stima dei parametri del processo generatore basandola sulla realizzazione disponibile costituita dalla serie storica. Poiché nell'ambito dei fenomeni sociali non è possibile ottenere più replicazioni della realizzazione mediante ripetizione dell'esperimento o dell'osservazione, stime consistenti possono ottenersi sotto particolari condizioni di ergodicità del processo - per la media e la varianza si richiede che le stime temporali convergano in media quadratica verso i rispettivi parametri - su cui non ci soffermiamo (v. Piccolo e Vitale, 1981, cap. 15.5); una condizione sufficiente per l'ergodicità rispetto alla media è che la sua funzione di autocorrelazione tenda a zero.I processi stocastici, che nella moderna analisi delle serie storiche svolgono un ruolo basilare, possono essere stazionari e non stazionari. Le condizioni della cosiddetta stazionarietà debole richiedono che la media μ e la varianza σ² siano finite e costanti al fluire del tempo, e che l'autocovarianza fra le variabili casuali in due punti-tempo t e t + τ sia una funzione γ(τ) - funzione di autocovarianza - che dipende solo dal ritardo τ e non da t. Quest'ultima condizione implica che il grafico della funzione (covariogramma) abbia la stessa forma indipendentemente dal punto-tempo da cui si inizia il calcolo; peraltro, la funzione γ(τ) e la funzione di autocorrelazione ϱ(τ) - espressa dal rapporto γ(τ)/γ(0), con γ(0) = σ², che normalizza γ(τ) e indica, al variare di τ, la correlazione della variabile con se stessa traslata al ritardo τ - sono funzioni pari (simmetriche), per cui i loro grafici sono limitati di solito ai soli valori τ ≥ 0. Un processo stocastico fondamentale nelle analisi di serie storiche è il cosiddetto rumore bianco (white noise, siglato WN): esso ha media nulla, varianza costante σ² e funzione di autocovarianza anch'essa nulla per τ ≠ 0; quest'ultima condizione assicura l'indipendenza delle variabili casuali componenti il processo. Alle funzioni sopra definite si associa anche la funzione di autocorrelazione parziale α(τ), definita per τ ≥ 2 dalle correlazioni fra i residui che si ottengono regredendo sia xτ+₁ che x₁ rispetto alle osservazioni intermedie x₂...xτ. Il vantaggio dei modelli costruiti per processi stazionari deriva dalla loro stabilità, poiché le loro proprietà statistiche sono indipendenti dal tempo; le serie storiche riguardanti fenomeni sociali sono quasi sempre non stazionarie: tuttavia la rappresentazione e l'analisi possono restringersi, previa eliminazione dei trends che generalmente sono presenti in esse, essenzialmente ai processi stazionari (v. cap. 5).
Se ϱ(τ) è una funzione di autocorrelazione, esiste una funzione ψ(ω) definita tra -π e π, che è la funzione di densità spettrale del processo stesso (v. § 4c). L'analisi dell'autocorrelazione, dell'associata matrice di Toeplitz (v. Piccolo e Vitale, 1981, p. 486) e della funzione di autocorrelazione parziale consente lo studio delle serie storiche e dei processi generatori nella loro dinamica temporale, mentre l'analisi spettrale, fondata sulla funzione di densità spettrale, ne studia la dinamica - in virtù del teorema di decomposizione della varianza (v. § 4c) - mediante l'individuazione di componenti periodiche stocastiche attribuendo a ciascuna frequenza angolare ω un contributo nella spiegazione della varianza totale del processo; i due approcci sono duali ed equivalenti.

b) Analisi temporale dei processi stazionari: i processi ARMA
Nel 1927 Slutzky mostrò che applicando un filtro lineare MA del tipo media mobile a un rumore bianco nasceva un ciclo stocastico: prima d'allora le medie mobili venivano usate disinvoltamente senza sospettare l'insorgenza di oscillazioni spurie; ne consegue che da un rumore bianco, che non ha memoria, può essere costruita qualunque altra serie attraverso filtri lineari specifici che modificano le densità spettrali. Indipendentemente e quasi in contemporanea Yule giunse alle stesse conclusioni, scoprendo peraltro che ogni serie storica connessa a un processo stazionario intrinsecamente stocastico si può trasformare in un rumore bianco eliminando per differenza la sua dipendenza dal passato, cioè la sua storia rappresentata dai valori ritardati inerenti ai tempi t-1, t-2..., ecc.: trasformazione formalizzata dai cosiddetti modelli autoregressivi AR. L'analisi temporale e la costruzione di modelli di processi stazionari hanno come riferimento fondamentale il teorema di Wold, il quale afferma che ogni processo stocastico stazionario {Xt} di media μ può esprimersi come somma di due processi stazionari e incorrelati: Xt = Vt + Zt, di cui il primo costituisce la cosiddetta componente deterministica o singolare e il secondo la componente puramente aleatoria o regolare:

formula

ove aj e bj sono successioni di variabili casuali a media e covarianza nulla, ωj una successione di numeri reali non negativi e in modulo minori di π (frequenze angolari deterministiche), mentre {εt,εt_-₁,..} è un rumore bianco (0, σ²). Valutate le frequenze angolari mediante l'analisi spettrale e approssimata la serie a un numero finito di termini, aj e bj possono essere stimati statisticamente, e la componente Vt eliminata per differenza; tuttavia, generalmente il peso di Vt non è rilevante e la componente singolare può essere trascurata. L'analisi si riconduce pertanto alla sola componente regolare Zt che può essere approssimata da un processo media mobile MA(q) con un numero finito di termini in quanto i coefficienti θj tendono a zero; utilizzando l'operatore ritardo 'Lag' definito da Lmεt = εt-m , con L⁰εt = εt, il processo può essere analiticamente rappresentato da Zt = θ(L)εt, ove θ(L) = 1 - θ₁L - θ₂L²... - θqLq. Tuttavia, la sua funzione di autocovarianza non caratterizza univocamente il processo, poiché esistono 2q processi del tipo MA(q) con la medesima funzione: la corrispondenza tra funzione di autocovarianza e processo media mobile è biunivoca se è soddisfatta la condizione di invertibilità, e cioè se tutti gli zeri (reali o complessi) del polinomio θ(L) sono in modulo maggiori dell'unità, vale a dire esterni al cerchio unitario del piano complesso di Argand-Gauss. Se il processo è invertibile, esso può esprimersi in forma autoregressiva infinita, e approssimato da un processo autoregressivo AR(p) finito, che assume la forma Zt = ϕ₁Zt-₁ + ϕ₂Zt-₂+...+ϕpZt-p + εt ⇔ ϕ(L)Zt = εt e che è sempre invertibile ma non sempre stazionario, tranne nel caso in cui tutti gli zeri del polinomio ϕ(L) di grado p nell'operatore L siano in modulo maggiori di 1. L'andamento di molti fenomeni sociali può rappresentarsi mediante modelli AR(p), ove εt ha la natura di un 'processo di innovazione': essi spiegano il presente in funzione del passato, mentre i modelli MA(q) - in cui l'influenza di εt è temporanea e tende a scomparire al fluire del tempo - spiegano il presente come risultato di una successione di impulsi casuali indipendenti. Esistono processi, cosiddetti ARMA(p,q), che rispecchiano le caratteristiche di entrambi, e che sono espressi analiticamente da ϕ(L)Zt = θ(L)εt; essi costituiscono uno schema misto, invertibile se lo è MA(q) e stazionario se lo è AR(p) e sono giustificati dal fatto che combinazioni lineari di AR e MA sono modelli ARMA, e che le serie storiche di moltissimi fenomeni sociali, rese stazionarie, possono descriversi mediante modelli misti. I modelli ARMA sono stati estesi in senso vettoriale per la rappresentazione delle interrelazioni esistenti tra più variabili stimando simultaneamente i parametri di uno schema vettoriale autoregressivo-media mobile, siglato VAR. Un secondo filone riguarda la trasformazione mediante il filtro di Kalman degli schemi ARMA e a livellamento esponenziale nella cosiddetta 'rappresentazione markoviana' (v. Carlucci, 1991, p. 415).
Se un processo ARMA è stazionario e invertibile, la sua valutazione si ottiene con procedure statistiche efficienti. Un metodo razionale è quello suggerito da G.E.P. Box e G.M. Jenkins (v., 1970), articolato in tre fasi: 1) identificazione del modello in base al 'principio di parsimonia' dei parametri, specificando gli ordini p e q mediante le funzioni γ(τ), ϱ(τ) e α(τ) che ne esprimono la struttura; 2) stima dei parametri del modello e verifica delle ipotesi; in particolare, con l'assunzione di normalità il processo è pienamente determinato nella sua struttura probabilistica e viene applicata una versione approssimata - con procedure iterative di calcolo numerico - del metodo della massima verosimiglianza; 3) controllo diagnostico, attraverso l'analisi dei residui, per la verifica della coerenza globale. Il metodo, malgrado il suo contenuto in gran parte meccanicistico, possiede una notevole potenzialità, ma richiede serie piuttosto lunghe, raramente disponibili in termini di omogeneità e confrontabilità dei dati, anche per le frequenti modificazioni definitorie e tecniche che caratterizzano le rilevazioni statistiche in campo sociale; inoltre, la complessità e delicatezza di molti aspetti della procedura richiede, per un impiego corretto ed efficace, un'elevata specializzazione. L'approccio di Box e Jenkins non ha tuttavia risolto in forma soddisfacente il problema di pervenire alla separazione delle componenti di un processo (v. Piccolo e Vitale, 1981, cap. 20).

c) Analisi spettrale dei processi stazionari
L'analisi spettrale - duale di quella temporale e parte integrante dell'analisi moderna delle serie storiche - è applicata fruttuosamente (ma piuttosto limitatamente nell'area sociale ed economica) nello studio delle serie stazionarie (o rese stazionarie) di vari fenomeni; essa costituisce un modo alternativo, ma complementare, di esplorare un processo stocastico, e presenta numerosi vantaggi sia nell'analisi di processi stazionari multivariati, sia quando si deve operare su vasti insiemi di dati. Il problema comune nel dominio frequenziale è la scomposizione spettrale, cioè l'identificazione delle oscillazioni di maggior frequenza che spiegano la varianza di una serie storica osservata. Punti di riferimento sono: a) il teorema di Harald Cramer, che afferma la rappresentabilità di ogni serie stazionaria a valori discreti mediante la somma di infinite oscillazioni cicliche statisticamente indipendenti, aventi ciascuna ampiezza e fase aleatorie ma periodo - e frequenza - fisso (si tratta in sostanza della decomposizione di Fourier trasferita nell'ambito dei processi stocastici); b) il teorema di scissione della varianza totale della serie come somma delle varianze delle singole componenti cicliche, impiegando la funzione di densità spettrale, che è la trasformata coseno di Fourier della funzione di autocovarianza, contiene le stesse informazioni e consente di valutare la funzione di guadagno di eventuali filtri; la differenza è nel diverso modo di pensare la serie: in termini di autocorrelazioni o in termini di frequenze. Lo spettro di frequenza, che ne costituisce il grafico, è lo strumento fondamentale dell'analisi spettrale, poiché dall'esame del suo andamento, e specialmente dei suoi picchi (massimi relativi), è possibile identificare le più importanti componenti oscillatorie presenti nella serie storica. Lo spettro può interpretarsi in termini di valore medio: operando su segmenti della serie e mediando si perviene alla stima della funzione di densità spettrale; l'estensione del periodogramma a struttura probabilistica si esplicita, nel dominio temporale, nell'uso di finestre basate su medie ponderate delle autocovarianze, e in quello spettrale di finestre basate sul livellamento del periodogramma (finestre di Bartlett, Parzen, ecc.; v. Priestley, 1981); le due finestre sono duali.

5. Serie storiche non stazionarie e relazioni tra serie storiche
Per i fenomeni reali, e in particolare per quelli dell'area sociale, gli andamenti delle serie storiche e i processi generatori sono quasi sempre evolutivi, con valore medio e varianza crescenti o decrescenti nel tempo; i coefficienti di autocorrelazione tendono lentamente a zero. Nelle analisi preliminari e successive è importante sottoporre a verifica l'ipotesi di stazionarietà anche quando non appare in evidenza un trend deterministico: a tal fine sono utilizzati vari test cosiddetti 'delle radici unitarie', fra cui quelli di Phillips e Perron e di Phillips e Ouliaris e specialmente il test di Dickey e Fuller, che sostituisce la tradizionale t di Student non più valida quando sono presenti nel modello valori ritardati della variabile dipendente. Quando un processo non è stazionario in media, la serie storica può essere suddivisa in segmenti da modellarsi separatamente. Se la media evolve secondo un polinomio di grado d, il processo stazionario in media può ottenersi come residuo dopo aver stimato ed eliminato il polinomio. Un'alternativa consiste nel trasformare i dati con un idoneo filtro in modo che l'output sia stazionario; se, applicando l'operatore ∇ consecutivamente d volte, viene generato un processo stazionario in media del tipo ARMA, il processo si dice integrato di ordine d e si indica con I(d). Ciò porta a considerare i processi ARIMA (processi ARMA integrati) definiti dalla seguente relazione: ∇dZt = WNt ~ ARMA(p, q), la cui tecnica operativa di identificazione e stima rientra nella procedura di Box e Jenkins. La non stazionarietà in varianza (eteroschedasticità) può attenuarsi trasformando logaritmicamente i dati se positivi; in termini euristici, per la scelta del tipo di trasformazione risulta molto utile l'impiego della trasformazione di Box e Cox (v. Harvey, 1993). Per quanto concerne la non stazionarietà in covarianza, essa non viene solitamente presa in considerazione, a meno che non sia possibile una scissione della serie in segmenti omogenei.
Le relazioni fra serie storiche possono essere esplorate nelle due ottiche della correlazione e della regressione. Nel primo caso, oltre le funzioni di autocovarianza di ciascuna di esse, svolgono un ruolo fondamentale la funzione delle covarianze incrociate - per due processi {Xt}, {Yt} si ha γxy(τ) = cov(Xt,Yt+τ) la cui trasformata di Fourier è la funzione di densità spettrale incrociata - e la funzione delle correlazioni incrociate; completano la strumentazione i grafici associati rappresentati dallo spettro incrociato o cross-spettro, dal co-spettro per la sola parte reale e dallo spettro di quadratura per la parte immaginaria. L'impiego è rivolto principalmente, nell'ambito dei sistemi lineari (v. Chatfield, 1984, pp. 186 ss.), a modelli di funzioni di trasferimento per l'analisi di relazioni dinamiche fra input e output. Nel contesto dei modelli ARIMA è possibile rappresentare le relazioni lineari esistenti fra una variabile Yt e k altre variabili Xit mediante un ampliamento del modello di Box e Jenkins: il modello modificato consente di rappresentare anche l'effetto di variabili d'intervento di politica sociale ed economica (v. Carlucci 1991, cap. 7).
Per quanto attiene ai modelli di regressione, è innanzitutto da osservare che le assunzioni poste alla base delle relative procedure di stima prevedono regressori deterministici o, se si tratta di variabili casuali, regressori stazionari. Nelle cosiddette 'regressioni statiche' del tipo Yt=α+ΣβiXit+εt fra variabili contemporanee, l'impiego di variabili integrate toglie validità alle dette ipotesi di base generando sovente regressioni spurie, mentre talune variabili 'test', quali la t di Student, non seguono le note distribuzioni standard; in ogni caso, quando le variabili storiche coinvolte sono integrate - specialmente se di diverso ordine - le relazioni sono generalmente sbilanciate e il residuo non può essere stazionario se non nei casi particolari in cui le variabili siano cointegrate. La questione può essere parzialmente superata riparametrizzando il modello mediante l'operatore ∇ o applicando la procedura di Cochrane e Orcutt: i due metodi, peraltro asintoticamente equivalenti, presentano tuttavia vari inconvenienti. Il miglior modo è di introdurre nell'equazione di regressione uno o più valori ritardati della variabile dipendente e di quelle esplicative, pervenendo al modello ARDL (autoregressivo a ritardi distribuiti), espresso da:

formula

(per due variabili), con A(L) e B(L) polinomi nell'operatore L di grado m e p; in tal caso il metodo dei minimi quadrati produce quasi sempre stime consistenti dei parametri (v. Hamilton, 1994, pp. 561-562). In effetti, mentre le teorie economico-sociali si esprimono assai spesso in termini di equilibrio, i dati storici osservati riflettono generalmente posizioni di breve periodo: l'incorporazione dei ritardi nella modellazione regressiva, esprimendo la memoria storica dei fenomeni considerati nei rispettivi valori correnti e quindi il grado d'inerzia presente nel loro movimento temporale, costituisce un modo efficace di rappresentare gli scostamenti di breve termine dalla relazione di equilibrio, espressa nel caso di due variabili dalla relazione di lungo periodo A(1)Y = m + B(1)X.
Le due variabili sono cointegrate C(d,d) se sono entrambe integrate I(d) di ordine d e se esiste una loro combinazione lineare - con coefficienti 1 e -c che sono le componenti del cosiddetto vettore di cointegrazione - tale che Yt - ψXt sia un processo I(0) e quindi stazionario. Pertanto, se le due variabili sono cointegrate, ∇Yt e ∇Xt sono stazionarie, e se lo è anche la differenza suddetta, denominata meccanismo di correzione dell'errore, la procedura tradizionale di stima regressiva è legittimamente applicabile sul modello ARDL riparametrizzato in una forma in cui compaiono solo le variazioni di Yt e di Xt o di loro valori ritardati e il meccanismo di correzione stimato sulla base della relazione di lungo periodo. La teoria della cointegrazione è estensibile senza difficoltà a regressioni con più variabili esplicative; in tal caso, per la verifica della cointegrabilità e la determinazione del vettore di cointegrazione è preferibile seguire la procedura indicata da S. Johansen applicabile a una formulazione VAR (v. Banerjee e altri, 1993). (V. anche Simulazione, modelli di).

bibliografia

Banerjee, A., Dolado, J., Galbraith, J.W., Hendry, D.F., Cointegration, error-correction and the econometric analysis of nonstationary data, Oxford 1993.
Box, G.E.P., Jenkins, G.M., Time series analysis, forecasting and control, San Francisco 1970.
Carlucci, F., Analisi delle serie storiche: i modelli stocastici, in Statistica economica (a cura di G. Marbach), Torino 1991.
Chatfield, C., The analysis of time series: an introduction, London 1984.
Gambetta, G., Analisi delle serie storiche: i metodi classici, in Statistica economica (a cura di G. Marbach), Torino 1991.
Gottman, J.M., Time series analysis. A comprehensive introduction for social scientists, Cambridge 1981.
Hamilton, J.D., Time series analysis, Princeton, N.J., 1994 (tr. it.: Econometria delle serie storiche, a cura di B. Stizia, Bologna 1995).
Hannan, E.J., Multiple time-series, New York 1973.
Harvey, A.C., Time series models, Hemel Hampstead 1993.
Piccolo, D., Vitale, C., Metodi statistici per l'analisi economica, Bologna 1981.
Priestley, M.B., Spectral analysis and time series, London 1981.
Santamaria, L., Analisi delle serie storiche, Bologna 1981.
Tukey, J.W., Exploratory data analysis, New York 1977.