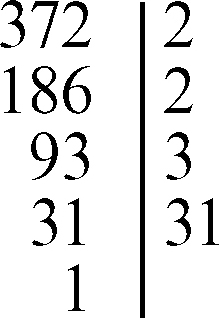Numero intero, scomposizione in fattori di un

numero intero, scomposizione in fattori di un

numero intero, scomposizione in fattori di un o fattorizzazione di un numero intero, in algebra, determinazione dei k interi n₁, ..., n_k, diversi da 1 e −1, il cui prodotto dia il numero n dato. Deve perciò essere n = n₁ ⋅ ... ⋅ n_k. In generale, un intero ammette più fattorizzazioni, ma ne esiste una privilegiata, la fattorizzazione in numeri primi. A meno del segno, tutti i fattori che compaiono in tale fattorizzazione sono necessariamente numeri primi. Ogni numero intero ammette una fattorizzazione in numeri primi; inoltre tale fattorizzazione è unica a meno di riordinamenti dei fattori e di eventuali moltiplicazioni per 1 e −1 (in modo da non alterare il segno del numero): questo è il contenuto del teorema fondamentale dell’aritmetica, il quale stabilisce il fatto che l’anello dei numeri interi Z è un dominio a fattorizzazione unica.

Canonicamente, una fattorizzazione in numeri primi si effettua raccogliendo i fattori ripetuti ed esprimendoli sotto forma di potenza, in ordine crescente; il segno del numero viene indicato all’inizio della fattorizzazione e i fattori che compaiono saranno tutti numeri positivi. Per esempio, la fattorizzazione di 2 è 2 = 2, poiché esso è un numero primo; la fattorizzazione di −1210 è invece −1210 = −2 ⋅ 5 ⋅ 11². L’algoritmo più comune (e il più costoso, da un punto di vista computazionale) per determinare la fattorizzazione in numeri primi di un dato intero n consiste nel determinare uno per uno, tramite verifica diretta o mediante l’uso di opportuni criteri di divisibilità, tutti i divisori primi dell’intero dato. Una volta determinato un divisore primo p, si effettua la divisione di n per p e si ripete il procedimento sul quoziente q = n /p: poiché i fattori primi di q sono fattori primi anche di n, procedendo in questo modo si determinano tutti i fattori primi di n.

Per esempio, per scomporre in fattori primi 372 si opera nel modo seguente, verificando la sua divisibilità per i successivi numeri primi:

Perciò 372 = 2² ⋅ 3 ⋅ 31. La conoscenza della fattorizzazione in numeri primi di un intero m fornisce molte informazioni sull’intero stesso: se per esempio m = ± p₁ⁿ₁ ... p_t ⁿ_t con p_i primo, allora il numero complessivo di divisori di m, compresi quelli banali, è (n₁ + 1) (n₂ + 1) ... (n_t + 1). Se a e b sono due interi di cui è nota la fattorizzazione in numeri primi, il calcolo del massimo comune divisore e del minimo comune multiplo è reso estremamente semplice: il mcd può essere calcolato effettuando il prodotto di tutti i fattori primi comuni ad a e b, elevati al minimo esponente con cui essi compaiono nelle due fattorizzazioni; il mcm invece può essere calcolato effettuando il prodotto di tutti i fattori primi comuni e non comuni ad a e b, elevati al massimo esponente con cui essi compaiono nelle due fattorizzazioni. Similmente, a partire dalle fattorizzazioni di a e b, è facile determinare quando a sia divisibile per b: ciò equivale al fatto che ogni fattore primo di a compaia nella fattorizzazione di b con esponente maggiore o uguale a quello con cui compare nella fattorizzazione di a.