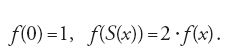La seconda rivoluzione scientifica: matematica e logica. Teoria della ricorsività

La seconda rivoluzione scientifica: matematica e logica. Teoria della ricorsivita

Teoria della ricorsività

La teoria della ricorsività affronta lo studio delle funzioni con lo scopo di classificarle dal punto di vista della loro difficoltà di calcolo. Una prima classificazione consiste nel distinguere le funzioni ricorsive (cioè, per definizione, quelle calcolabili mediante un computer) dalle altre. Ulteriori e più raffinate classificazioni si possono ottenere individuando varie altre classi di funzioni, alcune più estese e altre più ristrette della classe delle funzioni ricorsive.

I precursori

Nel 1837 Charles Babbage (1791-1871) progettò una macchina capace di essere programmata per effettuare tutti i calcoli che un essere umano può teoricamente eseguire. Egli si chiese quali operazioni fossero necessarie, e concluse che ci si può restringere a considerare alcune funzioni aritmetiche basilari (somma e prodotto) e alcune operazioni su di esse (ricorsione primitiva e ricerca del minimo, che definiremo più avanti). Egli aveva dunque concepito la nozione di funzione ricorsiva nel senso moderno, e un analogo di quella che si chiama tesi di Church, cioè l'asserzione che la nozione di funzione ricorsiva è un equivalente matematico preciso della nozione informale di funzione calcolabile.

Un'analisi matematica del concetto di numero naturale fu compiuta da Richard Dedekind (1831-1916) nel 1888. Egli iniziò notando che i numeri naturali sono generati a partire dallo 0, mediante l'operazione S (detta successore) tale che S(x)=x+1:

[1] 0, S(0)=1, S(S(0))=2 … .

Poiché i numeri sono tutti della forma 0 o S(x) (e non entrambe), Dedekind introdusse il principio di definizione per ricorsione primitiva: per definire una funzione su tutti i numeri naturali è sufficiente stabilire il suo valore per 0 e descrivere come si può passare dal valore per x al valore per S(x). Per esempio, la funzione f(x)=2^x si può definire nel seguente modo:

Dedekind era interessato a trovare proprietà che caratterizzassero la struttura dei numeri naturali in modo univoco, e scoprì che una struttura ordinata con un primo elemento e una funzione successore è indistinguibile dai (in termini tecnici, isomorfa ai) numeri numerali se soddisfa il 'principio del minimo', cioè se ogni suo sottoinsieme non vuoto ha un primo elemento. In tal caso è possibile stabilire l'isomorfismo per ricorsione primitiva (associando a 0 il primo elemento e a S(x) il successore dell'elemento associato a x), e il principio del minimo assicura che ogni elemento è immagine di un numero naturale. Dedekind non usò il principio del minimo, ma una sua forma equivalente detta 'principio di induzione'. Il principio del minimo ha però un'immediata controparte in termini di funzioni e quindi è più naturale dal nostro punto di vista.

Basandosi sull'analisi di Dedekind, Stephen C. Kleene (1909-1994) definì nel 1936 le funzioni ricorsive in modo induttivo, partendo dalla funzione costante 0 e dalla funzione successore S e generando nuove funzioni mediante ogni possibile combinazione di ricorsione primitiva e ricerca del minimo (che consiste nel trovare il minimo elemento di un insieme non vuoto di numeri naturali).

Consolidamento

Con il lavoro di Kleene terminò la fase di consolidamento della teoria della ricorsività, che occupò gli anni Venti e i primi anni Trenta del XX secolo.

Gli anni Venti videro soprattutto un'analisi della potenza della ricorsione primitiva e la conseguente scoperta dell'interesse della classe delle funzioni ricorsive primitive definite mediante tale procedimento. Attraverso i lavori di Paul Bernays, David Hilbert, Rózsa Péter e Thoralf Skolem si scoprì che non si ottengono nuove funzioni se si permettono procedimenti di definizione in cui il valore per S(x) si ottiene non soltanto dal precedente valore per x, ma da un numero qualunque di valori per 0,…,x. Una definizione primitiva ricorsiva di una funzione ne descrive il comportamento in modo tale da permetterne il calcolo.

La speranza che la classe delle funzioni ricorsive primitive contenga tutte (e sole) le funzioni calcolabili, cioè quelle per le quali esiste un procedimento che permetta di trovarne i valori in modo meccanico e in un tempo limitato, fu vanificata da Wilhelm Ackermann (1896-1962), che scoprì nel 1928 una funzione 'facilmente' calcolabile che non è ricorsiva primitiva, utilizzando un procedimento detto diagonalizzazione che risale a Georg Cantor (1845-1918).

Nei primi anni Trenta ci si cominciò a chiedere quale fosse allora la classe delle funzioni calcolabili. Alonzo Church, Kurt Gödel, Emil L. Post, Alfred Tarski e Alan M. Turing proposero diverse possibili definizioni. Ciascuna era basata su un particolare aspetto della nozione di funzione calcolabile: essere definibile attraverso un sistema di equazioni determinante i valori mediante semplici regole; ammettere dimostrazioni matematiche del fatto che un dato numero è il valore della funzione per dati argomenti; essere calcolabile mediante particolari macchine astratte, capaci di effettuare certe operazioni e prendere decisioni di vario tipo.

Ciascuno di questi modelli di calcolo poteva essere proposto come una soluzione matematica del problema di caratterizzazione della nozione di calcolabilità; si trattava però di fare una scelta convincente. L'imbarazzo non sussistette a lungo, poiché Kleene ottenne nel 1936 una serie di risultati che culminarono nella seguente sorprendente scoperta: tutte le definizioni proposte sono equivalenti e descrivono sempre la classe delle funzioni ricorsive.

Il metodo usato nelle dimostrazioni di tali risultati di equivalenza è detto aritmetizzazione, e consiste nell'assegnare numeri a oggetti in modo sistematico ed effettivo, e nel tradurre proprietà degli oggetti in proprietà dei loro corrispondenti numeri. L'osservazione cruciale fu però opera di Gödel, che notò come l'intero processo di aritmetizzazione si possa effettuare mediante funzioni ricorsive.

Naturalmente, l'equivalenza fra varie definizioni non era ancora una dimostrazione del fatto che la nozione di funzione ricorsiva fosse effettivamente una caratterizzazione della nozione di funzione calcolabile, ma certamente provava il grande interesse intrinseco della classe delle funzioni ricorsive.

I nuovi Prometei

Nel 1936 Church e Turing enunciarono la cosiddetta 'tesi di Church': le funzioni ricorsive sono esattamente le funzioni calcolabili. Post si spinse fino ad affermare che se il concetto di funzione ricorsiva è l'equivalente formale di quello di funzione calcolabile, la sua formalizzazione può giocare un ruolo nella storia della matematica secondo soltanto alla formalizzazione del concetto di numero naturale.

La tesi di Church è stata formulata in un eccesso di ottimismo, senza badare troppo alle sue possibili implicazioni. Essa ha certamente contribuito ad attirare l'attenzione sugli aspetti positivi della nozione di ricorsività, ma può oggi essere considerata come parte di quella guardia del corpo costituita di falsità di cui la verità ha bisogno di circondarsi.

Fra le varie definizioni equivalenti di funzione ricorsiva abbiamo citato la nozione di calcolabilità mediante macchine astratte. Tale approccio è dovuto a Turing e Post, e le cosiddette 'macchine di Turing' si possono oggi facilmente descrivere: esse sono i computer, qualora si prescinda dalle loro limitazioni fisiche (come la possibilità di guasti o di cattivo funzionamento, o la limitatezza di memoria). Qualunque computer (in tale senso astratto) è in grado di calcolare ogni funzione ricorsiva di cui gli sia fornito un programma. La tesi di Church afferma che le sole funzioni per cui esistono programmi sono le funzioni ricorsive e, dunque, che abbiamo raggiunto i limiti della potenza di calcolo meccanico: sarà possibile in futuro migliorare l'efficienza dei computer (per es., rendendoli più veloci) ma non la loro potenza assoluta. La teoria della ricorsività fornisce così uno strumento per dimostrare matematicamente limitazioni delle possibilità dei computer.

Non è una contraddizione aver detto che i computer non esistevano al tempo della formulazione della tesi di Church, ma che la definizione di funzione ricorsiva proposta da Turing e Post è equivalente alla calcolabilità mediante computer. La realtà è che, in questo caso, l'analisi teorica precedette la realizzazione tecnologica, e svolse un ruolo decisivo nei due progetti che portarono alla costruzione dei primi computer: l'ENIAC (electronic numerical integrator and calculator), diretto negli Stati Uniti da John von Neumann (1903-1957), e l'ACE (automatic computing engine), diretto in Gran Bretagna da Turing stesso, entrambi negli anni intorno al 1950. La tesi di Church non ha però soltanto applicazioni limitative delle possibilità dei computer. Usando la caratterizzazione delle funzioni ricorsive in termini di calcolabilità mediante computer, da essa si ottiene che le funzioni calcolabili lo sono mediante computer. Questa non è più un'asserzione di limitazione, bensì di potenza dei computer. Per comprenderla appieno, dobbiamo analizzare più da vicino cosa significhi l'aggettivo 'calcolabile'.

Una funzione è calcolabile da un punto di vista fisico se esiste un meccanismo che fornisce i suoi valori. Possiamo considerare come 'meccanismo' ogni sistema fisico che si evolva secondo le leggi fisiche oggi note. L'evidenza a disposizione non è tuttavia molto favorevole a questa versione fisica della tesi di Church. Già a livello di fenomeni descrivibili mediante le leggi della meccanica sussistono dubbi sulla sua accuratezza; per esempio, non si conoscono metodi effettivi per descrivere il comportamento di tre corpi soggetti all'azione di forze gravitazionali newtoniane.

Una funzione è calcolabile da un punto di vista umano se si possono ottenere i suoi valori mediante processi di calcolo cerebrali o mentali. Considerare cervello e mente come entità separate ci porta a discutere due conseguenze dell'affermazione che ogni funzione umanamente calcolabile è calcolabile da un computer. Per quanto riguarda il cervello, essa si traduce nell'affermazione che le attività cerebrali di natura logica o deduttiva si possono simulare mediante un computer. Norbert Wiener (1894-1964) e Turing hanno addirittura lasciato cadere ogni qualificazione, dando così inizio al sogno dell'intelligenza artificiale, nella forma: le attività cerebrali si possono simulare mediante i computer. Per quanto riguarda la mente, l'affermazione si traduce in: le attività mentali matematiche si possono simulare mediante un computer. Questa formulazione della tesi di Church si riferisce alla nozione di attività mentale matematica, oggetto di studi approfonditi da parte di Luitzen Egbertus Jan Brouwer (1881-1966).

Come già per il caso della calcolabilità fisica, l'evidenza a disposizione non è certo favorevole alla versione umana della tesi di Church. Soltanto a un livello estremamente rozzo (benché con conseguenze di grande utilità pratica) si può pensare di creare un parallelo fra cervello e macchine elettroniche. Nel 1943 Warren McCulloch (1898-1969) e Walter Pitts cercarono una prima approssimazione, avanzando alcune ipotesi semplificative sulla struttura e sul funzionamento dei neuroni: che essi siano componenti del sistema nervoso con risposte di tipo 'tutto o niente', aventi un livello di soglia fisso che determina la presenza o assenza di risposta, ed entranti in azione in modo sincronizzato a intervalli regolari quando la somma algebrica degli impulsi dei neuroni adiacenti raggiunge la soglia. McCulloch e Pitts provarono che un tale sistema si comporta realmente come una macchina (che essi chiamarono 'automa finito'), nel senso che ogni sistema di stimoli produce un'unica e determinata risposta.

Nonostante tali risultati positivi siano stati sostanzialmente migliorati negli anni seguenti, mostrando in particolare come ipotesi radicalmente meno restrittive di quelle precedenti producano ancora un comportamento deterministico, e dunque un modello di macchina che approssima meglio il comportamento reale del cervello, si è ancora ben lungi dal sogno fantascientifico di sintetizzare un vero cervello. In ogni caso, anche la realizzazione di una macchina che simuli completamente le funzioni cerebrali non dimostrerebbe né che il cervello è una macchina, né che la mente non esiste.

Sviluppo

Gli automi finiti trovarono un'applicazione immediata e fondamentale nella nascente industria dei computer. Turing aveva caratterizzato la nozione di calcolabilità nei termini di una scatola nera che fosse in grado di effettuare alcune operazioni elementari. Per l'effettiva costruzione di un computer restava da capire come una tale scatola nera fosse realizzabile, e il lavoro di McCulloch e Pitts fornì la chiave: un automa finito era sufficiente. In pratica un tale automa può essere sintetizzato mediante fili elettrici, le connessioni tra i quali sostituiscono i neuroni, e il passaggio o meno di una corrente elettrica determina la presenza o l'assenza di una risposta. Gli automi finiti, nati come modelli semplificati del cervello umano, divengono dunque cervelli elettronici per le macchine di Turing, rendendone possibile la costruzione.

I computer calcolano funzioni mediante programmi scritti in linguaggi di programmazione, dei quali esiste una grande varietà. La dimostrazione di equivalenza fra un dato modello di calcolo e la calcolabilità mediante computer consiste nel tradurre il metodo di calcolo di una funzione generica implicito nel dato modello in una serie di istruzioni eseguibili direttamente dal computer (il cosiddetto linguaggio macchina). In termini moderni, tale dimostrazione consiste nella costruzione di un cosiddetto compilatore. Essa fu effettuata per la prima volta da Turing e Kleene mediante il metodo di aritmetizzazione.

Una proprietà delle funzioni, assunta implicitamente nella trattazione finora esposta, è che esse attribuiscano un valore a ogni argomento. In termini tecnici, abbiamo considerato funzioni totali. Con l'avvento dei computer, però, le funzioni hanno ceduto il loro ruolo di oggetti privilegiati ai programmi o, in termini più astratti, ai metodi di calcolo. Un programma definisce una funzione in modo indiretto, stabilendo come calcolarne i valori, ma spesso non è semplice descrivere tale funzione direttamente. Un'altra conseguenza, dal nostro punto di vista più importante, è che un metodo di calcolo perfettamente definito non produce necessariamente un valore. Nel caso generale dei programmi, che descrivono semplicemente certi procedimenti di calcolo, non ci si può dunque aspettare che essi producano sempre un risultato. Per esempio, se si cerca di calcolare il valore f(0) usando il programma

si entra in un circolo vizioso: per calcolare f(0) si deve conoscere f(1), per calcolare f(1) si deve conoscere f(2), e così via.

Se si vuole attribuire un significato ai programmi in termini di funzioni bisogna quindi considerare funzioni parziali, che possono non assumere valori (essere indefinite) per certi argomenti (nei casi estremi, tutti o nessuno; le funzioni totali sono dunque particolari funzioni parziali).

Nel 1938 Kleene definì le funzioni parziali ricorsive, con una semplice modifica della definizione di funzione ricorsiva: egli permise la ricerca del minimo elemento di un insieme, senza più richiedere che l'insieme fosse non vuoto. Anche le altre definizioni delle funzioni ricorsive si possono adattare al caso delle funzioni parziali e si dimostra che le varie definizioni sono tutte equivalenti. In particolare, così come le funzioni ricorsive totali erano esattamente le funzioni totali calcolabili con computer, le funzioni ricorsive parziali sono esattamente le funzioni calcolabili con computer. Sia le funzioni ricorsive primitive sia le funzioni ricorsive parziali di un argomento si possono enumerare in modo effettivo, per esempio considerando tutti i programmi di un linguaggio di programmazione in ordine alfabetico. Si ottiene in questo modo una lista

[4] φ₀, φ₁, φ₂…

di tutte le funzioni ricorsive parziali di un argomento. Tale lista è essa stessa ricorsiva parziale, in quanto esiste un singolo programma di due argomenti capace di eseguire i calcoli di un qualsiasi programma di un solo argomento. Si ha così il cosiddetto 'teorema di enumerazione': la funzione

è ricorsiva parziale. Il teorema di enumerazione evidenzia un'importante proprietà della classe delle funzioni ricorsive parziali, e dimostra come tale classe abbia la capacità di 'descrivere sé stessa'. Dal punto di vista informatico, esso spiega come sia stato possibile passare da macchine per specifiche funzioni ricorsive (come le calcolatrici tascabili) a macchine universali per tutte le funzioni ricorsive (come i computer): queste ultime sono semplicemente macchine per la specifica funzione φ(x,z), e quindi calcolano indirettamente ogni φ_x, quando si fissi x.

La nozione di funzione ricorsiva parziale suggerisce in modo spontaneo la domanda se sia possibile accorgersi (per es., in modo ricorsivo) se un programma calcola una funzione totale. Tuttavia è facile notare che così non è. Il problema di decidere se un programma calcola una funzione totale non è ricorsivo; è stata proprio l'introduzione della nozione di funzione parziale ad aver permesso di ottenere il teorema di enumerazione. Il problema della totalità di una funzione è solo uno dei vari problemi senza soluzioni ricorsive, che la tesi di Church interpreta dunque come umanamente impossibili da risolvere. Il più famoso di tali esempi è il cosiddetto 'problema della fermata': decidere se una data funzione ricorsiva parziale è definita per un dato argomento o, equivalentemente, se un computer si ferma (e ottiene dunque un valore) quando calcola seguendo le istruzioni di un dato programma per un dato argomento.

L'insolubilità del problema della fermata si può formulare come segue: se un programma che fornisce risposte a domande riguardanti la fermata di dati programmi per dati argomenti non mente mai, esso non può fornire tutte le risposte. Poiché generalmente è facile rispondere in maniera affermativa a tali domande (semplicemente simulando il dato programma sui dati argomenti, e aspettando fino a che si ottenga un valore), la limitazione si ha nel caso di risposta negativa (nel qual caso la simulazione precedente non giunge mai a termine).

La formulazione appena descritta del problema della fermata mostra una grave limitazione delle capacità assolute dei programmi. Ciò appare ancora più grave quando si considerino i programmi in due modi complementari: da un lato, essi si possono codificare con i numeri, e dunque affermazioni sul loro comportamento sono, mediante aritmetizzazione, relative a proprietà dei numeri; d'altro lato, l'attività matematica che consiste nel derivare teoremi da assiomi mediante regole si può essa stessa codificare attraverso programmi. Possiamo allora riformulare ulteriormente l'insolubilità del problema della fermata, e ottenere una versione del 'teorema di Gödel': un sistema di assiomi e regole che sia codificabile mediante un programma e che non menta mai non può fornire risposte a ogni domanda riguardo ai numeri. In altri termini, il teorema di Gödel afferma che la verità matematica non può essere compressa né in sistemi assiomatici, né in programmi di computer.

I programmi dei computer definiscono funzioni mediante metodi di calcolo. Poiché però tali metodi riducono il calcolo di dati valori di una funzione al calcolo di altri valori della stessa funzione e mediante lo stesso metodo, c'è in essi qualcosa di circolare. Per esempio, il programma

[6] φ(x)≃φ(x)

non fornisce alcuna indicazione pratica su come si possa calcolare un qualunque valore di φ, e inoltre la condizione espressa da tale programma è soddisfatta da ogni funzione, parziale o totale che sia. In che senso dunque una funzione è definita da tale programma?

La risposta fu data da Kleene, che nel 1952 dimostrò il cosiddetto 'teorema di ricorsione'. Esso afferma che, nonostante le condizioni imposte da un programma possano essere soddisfatte da più di una funzione, il metodo di calcolo che consiste nel sostituire sistematicamente la parte sinistra di un'equazione con la parte destra definisce la minima di tali funzioni parziali (che è ricorsiva, in quanto calcolabile mediante un computer). In precedenza, nel 1938 Kleene aveva stabilito il cosiddetto 'teorema del punto fisso'. Secondo tale teorema ogni equazione che definisce una funzione, in cui la variabile sia un numero per un programma della funzione stessa, ammette una soluzione numerica (che codifica una funzione ricorsiva parziale).

Negli anni Trenta la teoria della ricorsività si orientò verso risultati sempre più tecnici, benché ancora motivati da problemi di natura generale. Dalla fine degli anni Quaranta quest'ultima tendenza prese il sopravvento, gli aspetti tecnici divennero predominanti e la teoria della ricorsività si trasformò in una branca della matematica a sé stante. La classificazione delle funzioni (totali) in ricorsive e non ricorsive è fondamentale, ma piuttosto grossolana: infatti, la maggioranza delle funzioni consiste di funzioni non ricorsive.

Nel 1939 Turing introdusse un metodo che permette di discriminare fra loro funzioni non ricorsive (e dunque problemi insolubili), e di distinguire vari gradi di insolubilità. L'idea consiste nel passare dalla nozione di calcolabilità assoluta, considerata finora, a quella di calcolabilità relativa a un certo oracolo, cui si possa chiedere aiuto durante un calcolo. Tale idea si può pensare come un'astrazione del processo interattivo uomo-macchina, in cui il computer ha la possibilità di demandare certe scelte al programmatore: tale possibilità è utile quando, per un qualunque motivo, non si voglia o non si sappia affidare ogni parte di un calcolo al computer.

Due problemi si dicono dello stesso grado se ciascuno si può risolvere usando l'altro come oracolo (ed essi hanno quindi la stessa difficoltà); un problema si definisce invece di grado inferiore a un altro se il primo è risolubile usando il secondo come oracolo, ma non viceversa (e dunque il primo è più facile da risolvere del secondo). Una buona parte dei risultati della teoria della ricorsività consiste nello studio, iniziato da Kleene e Post nel 1954, delle proprietà di struttura dei gradi. Per esempio, è ovvio che esiste un grado minimo (quello dei problemi che sono risolubili, senza chiedere aiuto a nessun oracolo; equivalentemente, quello delle funzioni ricorsive), mentre è meno ovvio che non ci siano problemi di grado massimo. Questo risulta per analogia con il (in termini tecnici, per relativizzazione del) fatto che il problema della fermata non è risolubile: dato un qualunque problema, si può considerarlo come un oracolo, e il problema della fermata per programmi che usino tale oracolo non è risolubile relativamente a esso (e ha, in realtà, grado maggiore). Ancor meno ovvio è che ci siano problemi con gradi inconfrontabili, e quindi di difficoltà incomparabile, o problemi con gradi minimali, cioè non risolubili, e tali che non possano fungere in modo utile da oracoli per nessun altro problema (gli unici problemi risolubili con tali oracoli sono quelli della stessa difficoltà, e quelli risolubili senza oracoli).

La struttura dei gradi si è rivelata estremamente complicata e quindi deludente, perché si sperava che il suo studio avrebbe potuto portare a una descrizione semplice dell'insieme di tutte le funzioni. Nonostante oggi si conosca molto sulla struttura dei gradi, una sua completa caratterizzazione non è ancora stata trovata.

Finora si è parlato di funzioni e di loro classificazioni. Tuttavia una gran parte della teoria della ricorsività consiste nello studio e nella classificazione degli insiemi di numeri, che possono essere visti come particolari funzioni a valori 0 e 1: tali valori si possono interpretare come risposte positive o negative alla domanda se un numero appartenga o no all'insieme dato. Anche per gli insiemi si può parlare di calcolabilità relativa e di loro gradi di insolubilità. Gli insiemi il cui grado è il più semplice possibile sono quelli detti ricorsivi, tali cioè che la funzione a essi associata sia ricorsiva. Essi sono dunque quelli per i quali un computer può determinare se un elemento appartenga o no all'insieme.

Un tipo particolarmente interessante di insiemi è quello degli insiemi ricorsivamente enumerabili, per i quali esiste una funzione ricorsiva che ne enumeri gli elementi. I loro elementi possono dunque essere enumerati da un computer. L'insolubilità del problema della fermata dimostra che esistono insiemi ricorsivamente enumerabili ma non ricorsivi. Poiché per ogni insieme ricorsivamente enumerabile esiste un programma x che si ferma sull'argomento z se e solo se esso sta nell'insieme, il problema della fermata ha il massimo grado fra quelli degli insiemi ricorsivamente enumerabili.

Nel 1944 Post si chiese se vi fossero soltanto due gradi di insiemi ricorsivamente enumerabili, cioè quello dei problemi risolubili e quello del problema della fermata. Tale questione divenne nota come 'problema di Post' e fu risolta negativamente nel 1956 da Richard Friedberg e Albert Muchnik, che idearono una modifica costruttiva del metodo di diagonalizzazione, detta metodo di priorità. Essi dimostrarono, in realtà, che anche in questo caso esistono insiemi di grado inconfrontabile.

La teoria dei gradi di insiemi ricorsivamente enumerabili è la parte più sofisticata e difficile della teoria della ricorsività, e la struttura di tali gradi è ancora più complessa e patologica di quella dei gradi in generale. A partire dalla fine degli anni Cinquanta, con un interesse via via crescente, la teoria della ricorsività ha cercato di svincolarsi dall'approccio puramente numerico e di estendere la propria ricerca alla nozione di computabilità su oggetti di varia natura. Una tale estensione è ovviamente richiesta quando si vogliano considerare operazioni sui numeri reali, come nell'analisi. Per poter parlare di calcolabilità di tali operazioni si deve estendere la nozione di calcolabilità da funzioni di numeri naturali a funzioni di numeri reali, e ciò ha portato allo sviluppo dell'analisi ricorsiva. Un tipico risultato dell'analisi ricorsiva, che mostra quanto essa possa scostarsi dall'analisi classica, è che ogni funzione ricorsiva di numeri reali è continua.