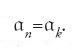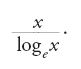La seconda rivoluzione scientifica: matematica e logica. Geometria algebrica
Storia della Scienza (2004)
La seconda rivoluzione scientifica: matematica e logica. Geometria algebrica
Geometria algebrica
Agli inizi del XX sec. la scuola di punta in geometria algebrica era quella italiana, guidata da Guido Castelnuovo, Federigo Enriques e Francesco Severi impegnati prevalentemente nella teoria delle superfici algebriche, allora in espansione, e nella classificazione delle superfici, in particolare Enriques e, indipendentemente, Giuseppe Bagnera e Michele De Franchis. Altrove, in Europa, i lavori avevano un carattere meno apertamente geometrico. In Francia si poneva maggiormente l'accento sui legami con l'analisi complessa, mentre in Germania si dava più peso all'aspetto algebrico. Queste due priorità riflettevano tradizioni dei singoli paesi, preludendo al modo in cui l'una o l'altra impostazione tenderà ad assumere un ruolo prevalente nella ricerca in questo importante e difficile campo della matematica moderna.
Fra Otto e Novecento
In Francia la figura preminente era Charles-émile Picard (1856-1941) che con Georges Simart pubblicò nel 1897 il primo volume della Théorie des fonctions algébriques, al quale seguirà un secondo volume nel 1906. Picard riassume in quest'opera i risultati di un notevole numero di lavori apparsi in un ampio arco di tempo estendendo, a prima vista in modo sorprendente, alle superfici algebriche l'approccio di Georg Friedrich Bernhard Riemann (1826-1866) alle curve algebriche. Egli classifica gli integrali semplici e doppi sulle superfici a seconda del tipo di singolarità, e mostra come tutto ciò sia strettamente legato ai lavori di Castelnuovo ed Enriques. Picard e Simart chiederanno in effetti ai due italiani un saggio che sarà pubblicato alla fine del secondo volume. Un punto saliente di quest'opera è l'estensione del teorema di Riemann-Roch al caso delle superfici, risultato che figurava già nei lavori della scuola italiana secondo un punto di vista prevalentemente geometrico.
Un altro importante matematico francese fu Georges-Marie Humbert (1859-1921), che si occupò dell'analogia tra superfici iperellittiche e classi di funzioni automorfe in due variabili. Le superfici iperellittiche sono un caso particolare, ma importante, di superfici; Humbert riuscì a dare una descrizione particolareggiata di molte delle loro proprietà e a fornirne una migliore classificazione.
I matematici tedeschi preferirono in generale un approccio algebrico, di due tipi. Il primo ebbe come pionieri Kurt Hensel (1861-1941) e Georg Landsberg (1865-1912), studenti di Leopold Kronecker (1823-1891). Essi svilupparono la teoria dei divisori in modo definitivo nella Theorie der algebraischen Funktionen (Teoria delle funzioni algebriche, 1902). Il termine 'divisore' è dovuto a Kronecker, l'impostazione della teoria allo stesso Kronecker e in ugual misura al lavoro congiunto di Richard Dedekind (1831-1916) e Heinrich Martin Weber (1842-1913) nei primi anni Ottanta del secolo. Nel caso di una curva algebrica vi è una corrispondenza biunivoca (a meno di un'equivalenza birazionale) tra la curva e il campo delle funzioni razionali su di essa definite, e ciò significa che ci si può limitare a studiare questo campo. Esso viene presentato come un ampliamento trascendente del campo complesso, seguito da un ampliamento algebrico (che corrisponde all'equazione della curva). I divisori figurano come insiemi finiti di punti contati con molteplicità positiva o negativa, che possono rappresentare, per esempio, gli zeri e i poli di funzioni razionali sulla curva. Si possono definire classi di divisori e ritrovare il teorema di Riemann-Roch in un ambito puramente algebrico. È possibile in realtà definire tutti gli aspetti della geometria di una curva nella teoria dei campi delle funzioni razionali.
Mentre per Kronecker il vantaggio di un approccio di questo tipo era legato alla sua concezione della matematica, altri l'apprezzavano per il suo grande rigore. Per alcuni anni intorno al 1900 la teoria delle curve algebriche si occupò prevalentemente di punti singolari. Era anche troppo facile avere un'intuizione geometrica sulla natura di questi punti e scoprire casi particolari di un certo interesse. La teoria dei divisori offriva affidabilità, anche se i legami con la geometria e l'analisi sembravano deboli.
La teoria dei divisori è molto meno rilevante nel caso delle superfici, alle quali non si estende l'isomorfismo tra curve e campi di funzioni razionali. Superfici non isomorfe possono avere lo stesso campo di funzioni. Per esempio, il piano proiettivo ℂℙ2 e una quadrica non degenere (che si può considerare come ℂℙ1×ℂℙ1) sono superfici birazionalmente equivalenti, e dunque hanno lo stesso campo di funzioni, ma non sono nemmeno omeomorfe. Occorre quindi specificare il passaggio inverso dal campo di funzioni alla superficie con qualche metodo ad hoc. Ciò è possibile, e fu così che il matematico tedesco Heinrich W.E. Jung poté dimostrare, nel 1905, il teorema di Riemann-Roch per le superfici. Con Jung si assiste a un progresso rispetto alla scuola italiana: per la prima volta sono infatti ammessi divisori negativi (che corrispondono a curve virtuali sulla superficie). Il suo lavoro fu salutato come la prima dimostrazione generale rigorosa di questo importante risultato.
Il secondo approccio alla geometria algebrica della scuola tedesca sviluppò, a partire dai lavori di David Hilbert (1862-1943) sulla teoria degli invarianti, una disciplina dotata di un'enorme quantità di metodi per calcolare proprietà di polinomi in più variabili invarianti per trasformazioni (come, per es., il cambiamento di variabili). Il problema principale richiedeva di calcolare gli invarianti di un dato polinomio e dimostrare che si possono ottenere tutti come polinomi in un numero finito di essi. Verso la fine del XIX sec. molti matematici, tra i quali Paul A. Gordan (1837-1912), affrontarono questo problema, ma la complessità dei metodi elaborati allo scopo era tale che fu possibile risolvere completamente soltanto il caso dei polinomi in due variabili.
In una serie di importanti lavori dei tardi anni Novanta del XIX sec., Hilbert aggirò completamente queste difficoltà operando a un livello più concettuale. Riflettendo su cosa avrebbe significato potere esprimere tutti gli invarianti in termini di un numero finito di essi, dimostrò che si può sempre costruire un tale insieme finito di invarianti e che il procedimento di costruzione termina dopo un numero finito di passi. Ciò permette di stabilire l'esistenza di una base finita per gli invarianti con un metodo così semplice che Gordan sulle prime era incline a rifiutare: affermò infatti che si trattava di teologia, non di matematica. Più tardi cambiò idea. Hilbert sviluppò il proprio metodo in modo da renderlo esplicito in ogni singolo caso, favorendo il superamento dell'intricata situazione che aveva bloccato i tentativi precedenti.
Egli si esprimeva nel linguaggio allora emergente degli anelli e degli ideali, che aveva imparato studiando i lavori di Dedekind sulla teoria algebrica dei numeri. Questi concetti, se appaiono piuttosto distanti dalla geometria algebrica, hanno però il vantaggio di funzionare bene in qualunque numero di variabili, ossia, in termini geometrici, in qualunque dimensione. Come si è visto, l'approccio puramente geometrico era allora confinato a curve e superfici. I metodi di Hilbert si univano quindi fruttuosamente a quelli di Kronecker, che molto si era adoperato per sviluppare una teoria algebrica delle varietà algebriche in un qualunque numero di variabili.
Più sorprendente è osservare come la scuola dei matematici raccolti attorno a Felix Christian Klein (1849-1925) si sia occupata relativamente poco di geometria algebrica. Alcuni studenti di Klein lavorarono su classi particolari di superfici, spesso in relazione con i numerosi modelli di superfici costruiti a scopo didattico. L'interesse specifico di Klein era però rivolto soprattutto alla teoria delle funzioni abeliane, e sempre di più alla matematica applicata. Pertanto egli diresse poche tesi di dottorato in geometria.
Uno dei più importanti studiosi di geometria algebrica fu Solomon Lefschetz (1884-1972), nato a Mosca, figlio di cittadini turchi che si erano trasferiti a Parigi. Di lingua madre francese, imparò molte lingue, compreso il russo. Studiò ingegneria a Parigi e nel 1905 emigrò in America; nel 1907 un'esplosione sul luogo di lavoro gli costò la perdita di entrambe le mani. Riuscì a riprendersi da questa tragedia e ritornò alla matematica; si iscrisse quindi alla Clark University a Worchester, nel Massachusetts, dove scrisse in un anno la tesi di dottorato in geometria algebrica. Per molti anni insegnò alla University of Kansas a Lawrence, sfruttando l'isolamento per approfondire i suoi interessi nella materia. Il riconoscimento internazionale doveva infine valergli, nel 1924, un invito a Princeton dove trascorse il resto della sua carriera.
Il contributo principale di Lefschetz sta nell'aver stabilito l'importanza della topologia nello studio della geometria algebrica, in particolare nello studio delle varietà di dimensione superiore. Lefschetz aveva letto approfonditamente l'opera di Picard e Simart e aveva cercato di generalizzare il loro lavoro sugli integrali applicando le idee di Jules-Henri Poincaré sulla topologia delle varietà in questo ambito geometrico. Egli riuscì a separare la descrizione topologica di una superficie complessa da quella, più problematica, espressa in termini di teoria delle funzioni. Dimostrò così, tra l'altro, che non tutte le varietà (di dimensione reale pari) possono essere varietà algebriche complesse.
Il periodo 1918-1939
Dopo la Prima guerra mondiale la situazione nella geometria algebrica cambiò notevolmente. In Italia, Castelnuovo era passato ad altri argomenti (tra i quali la teoria della probabilità e quella della relatività), anche se dietro le quinte continuava a esercitare una forte influenza. I ricercatori più attivi erano allora Enriques, Severi e Gino Fano (1871-1952). Tra questi, Enriques era soprattutto impegnato a perfezionare quanto sulle superfici era già noto, con l'intenzione di promuovere il suo punto di vista sull'intuizione matematica come modo proficuo di fare ricerca. Severi diventò gradualmente il portavoce dei geometri italiani. I suoi lavori erano dedicati in gran parte a problemi difficili di geometria enumerativa e a rendere rigoroso quanto era stato fatto prima della guerra. Fano, con l'aiuto di Severi, aprì la strada per estendere alle varietà algebriche di dimensione complessa 3 quanto era stato elaborato per le superfici.
Schematicamente si può affermare che il lavoro di questa generazione di matematici italiani fu segnato, da un lato, da notevoli intuizioni e, dall'altro, da significativi fallimenti. Severi non riuscì a definire un metodo generale per affrontare i problemi che inevitabilmente si sarebbero presentati in futuro, come egli acutamente aveva previsto. Fano si serviva di metodi del cui rigore cercava invano di convincere gli altri. La svolta decisiva si fa risalire convenzionalmente al soggiorno romano di Oscar Zariski (1899-1986). Egli era un ebreo russo con passaporto polacco che giunse nel 1921 in Italia. Su suggerimento di Enriques cambiò il nome (che era Ascher Zaritsky), e, infine, partì per gli Stati Uniti non tanto per il nascente antisemitismo in Italia quanto per il consiglio di Castelnuovo di andare a studiare con Lefschetz. Negli Stati Uniti soggiornò per tutto il 1927 (per un mese studiò con Lefschetz), prima di emigrarvi definitivamente l'anno dopo.
Fu subito chiaro comunque che gli standard di rigore di Zariski erano superiori a quelli dei suoi maestri italiani. Egli amava ripetere quanto Castelnuovo gli aveva detto una volta "Lei sta qui con noi, ma non è uno di noi": il libro che scriverà nel 1934, Algebraic surfaces, fu un modo di saldare i conti.
Per offrire una descrizione veramente rigorosa della teoria dei punti singolari e delle curve su una superficie, che a suo avviso doveva essere il punto di partenza della disciplina, Zariski non soltanto si impadronì completamente dell'impostazione italiana, ma cominciò anche a sospettare che essa avesse un vizio di fondo. Si allontanò da quei metodi decisamente geometrici e iniziò a sostituirli con quelli di Lefschetz. Il libro prende così le mosse dalla teoria delle singolarità e del loro scioglimento e, utilizzando la teoria dei sistemi lineari della scuola italiana e il teorema di Riemann-Roch per le superfici, giunge alla definizione delle proprietà topologiche delle superfici e alla teoria degli integrali semplici e doppi, nella quale è evidente l'influenza di Lefschetz.
Zariski sentiva che gli sforzi fatti nel presentare la teoria italiana erano "la perdita personale del paradiso geometrico nel quale aveva vissuto". Per ottenere insieme un adeguato rigore e una sufficiente generalità, egli sentiva di dover guardare oltre la teoria di Lefschetz (che riguarda le varietà complesse) verso i metodi puramente algebrici dell'algebra noetheriana. Cominciò con la Idealtheorie (1935) di Wolfgang Krull (1899-1971), e presto si accorse che, contrariamente all'opinione dello stesso Krull, quella teoria poteva essere utile nello studio delle singolarità.
Emmy Noether (1882-1935) aveva sviluppato un proprio modo di vedere l'algebra, nuovo e profondo, per promuovere sia la geometria algebrica sia la teoria algebrica dei numeri. L'idea era di creare metodi generali astratti, più semplici da utilizzare di quelli che erano allora a disposizione, spesso appesantiti da troppi dettagli inessenziali. Ella sviluppò queste idee assieme ad alcuni giovani colleghi, anch'essi eccezionalmente dotati. Tra questi, il matematico olandese Bartel Leendert van der Waerden (1903-1996) era il più interessato alla geometria algebrica. La Noether elaborò le idee di Hilbert su anelli e ideali e le trasformò in una teoria della decomposizione degli anelli che soddisfa la condizione detta 'della catena ascendente': ogni catena ascendente di ideali primi è finita. Siccome nel passaggio dalla geometria all'algebra gli ideali primi corrispondono alle sottovarietà, quella condizione coincide con il fatto naturale che possono esistere soltanto catene finite di varietà di dimensioni sempre più piccole.
L'approccio della Noether fornisce quello che potremmo chiamare un dizionario tra oggetti geometrici e oggetti algebrici. La cosa più semplice è cominciare con le curve piane e modificare passo dopo passo la teoria del XIX secolo. Nell'anello k[x,y] dei polinomi in due variabili si associa a una curva C l'ideale I(C) dei polinomi che si annullano su C. L'anello delle coordinate affini A(C) della curva è il quoziente dell'anello k[x,y] per l'ideale I(C). Se due funzioni di A(C) sono distinte, allora esistono punti della curva nei quali esse assumono valori diversi. L'anello A(C) dà luogo al campo dei quozienti dell'anello, in modo analogo a come l'anello degli interi genera un campo dei numeri razionali. Alla curva restano in questo modo associati sia un anello sia un campo di funzioni.
Fin qui queste costruzioni si applicano a ogni curva, ma per distinguere tra curve singolari e non singolari occorrono oggetti algebrici più raffinati. In un punto ordinario P di una curva, le rette per P incontrano la curva una sola volta, esclusa la tangente che l'incontra due volte. Ma una retta per un punto doppio l'incontra due volte, e le tangenti a ciascuno dei suoi rami tre volte. L'idea è che in un punto ordinario della curva la tangente è simile alla curva, mentre in un punto singolare questa somiglianza viene meno. Gli oggetti algebrici che si costruiscono sono gli 'anelli locali'. Pertanto l'anello locale in un punto P di una curva è l'anello OP delle classi di equivalenza delle funzioni regolari (definite sugli aperti della curva che contengono P), dove due funzioni sono equivalenti se coincidono sui punti della curva nei quali sono definite.
L'anello locale OP contiene un unico ideale massimale mP che consta delle funzioni regolari che si annullano in P. Lo spazio tangente in P è legato allo spazio quoziente mP/(mP)2, che nei punti non singolari è grosso modo lo spazio dei valori delle derivate prime. Se il punto P è non singolare, la dimensione dello spazio mP/(mP)2 è uguale a quella del campo dei resti A(C)/m, mentre se P è singolare è maggiore.
Molte di queste idee furono facilmente generalizzate dalla Noether e da altri matematici a varietà di dimensione superiore. Vi è uno stretto legame tra ideali di un anello di coordinate e varietà algebriche: lo stabilisce in un senso tecnico preciso il Nullstellensatz (teorema degli zeri) di Hilbert. È spesso importante sapere, per esempio, se una varietà è connessa o no. In geometria algebrica ciò significa decidere se è possibile definire la varietà per mezzo di un solo polinomio irriducibile (ossia non fattorizzabile) o no. Una varietà irriducibile dà luogo a un ideale primo di A. Un ideale di un anello si dice massimale se non vi sono ideali strettamente compresi tra l'ideale stesso e tutto l'anello. Questi ideali corrispondono a punti della varietà. Una varietà V′ contenuta in una varietà V (una sottovarietà di V) corrisponde a un ideale I(V′) di A che contiene necessariamente I(V). Questo legame tra catene discendenti di varietà e catene ascendenti di ideali può essere definito con precisione.
Nei primi anni Venti del XX sec. la Noether pone l'accento sul procedimento inverso: partire da un anello commutativo e fare geometria facendo dell'algebra. Negli anelli da lei considerati ogni catena ascendente di ideali è finita, cioè da un certo punto in poi la catena termina con una uguaglianza: se
Ciò corrisponde al fatto geometrico evidente che non vi può essere una catena discendente infinita di sottovarietà di una varietà. Questi anelli si incontrano ovunque, e meritano quindi un nome: vengono detti 'noetheriani', in onore appunto di Emmy Noether.
La 'dimensione' di un anello è la lunghezza della catena più lunga di ideali primi (la dimensione dell'anello kn è fortunatamente n). Questa idea della dimensione è stata introdotta nel 1928 da Krull il quale esercitò una notevole influenza nell'attirare l'attenzione sul concetto generale di anello noetheriano. Per mezzo della teoria degli ideali, Krull dimostrò che le dimensioni delle componenti irriducibili di una varietà algebrica in uno spazio affine di dimensione n definite da d equazioni sono almeno uguali a n−d.
Nel 1932 Krull introdusse la teoria delle valutazioni additive. Il concetto di valutazione, che risale a Dedekind e Weber, formalizza quello di grado di una funzione in un punto, e fu introdotto per permettere il passaggio dal campo di funzioni associato alla curva ai punti della curva. In realtà, a partire dal campo di funzioni si possono ottenere i punti come zeri e poli delle funzioni: sono i punti della curva nei quali le valutazioni sono non nulle. Dedekind e Weber non riuscirono a trovare il modo di introdurre una topologia nell'insieme di tutte le valutazioni associate a un campo di funzioni. Krull estese il concetto di valutazione in modo che potesse assumere valori in un gruppo ordinato qualunque, e dimostrò che gli anelli di valutazione costituiscono un'utile generalizzazione degli anelli noetheriani. Zariski li utilizzò per affrontare con successo il problema di sciogliere le singolarità delle superfici definite su campi di caratteristica zero.
Il problema del quale si occupò maggiormente Severi, e che doveva essere il bersaglio principale delle aspre critiche di van der Waerden, era quello di definire la molteplicità di un'intersezione. Nei casi più semplici il problema è abbastanza chiaro. Per esempio, se una curva ne interseca un'altra in un punto, e le tangenti alle due curve in quel punto sono distinte, allora la molteplicità di intersezione è 1. Cosa succede però se il punto di intersezione è un punto multiplo per una delle due curve? O se le tangenti alle due curve non sono distinte? Singolarità complesse come queste notoriamente costituiscono un problema già per le curve: le singolarità di superfici e di varietà di dimensione superiore possono essere ancora più difficili da trattare. Per la Noether si dovevano tradurre le complicazioni geometriche in complicazioni algebriche, da risolvere con i nuovi metodi.
È la filosofia che Zariski adottò con decisione. Molte delle idee che egli introdusse nella teoria degli anelli commutativi si possono considerare come tentativi di formulare questa o quella proprietà delle varietà. Tuttavia, per quanto amasse l'algebra, e per quanto importanti e duraturi siano stati i suoi contributi, egli sentiva sempre la geometria come il centro dei suoi interessi ("la geometria è la vera vita" soleva affermare). Così, per esempio, egli diede una caratterizzazione dei punti singolari che dimostrava come il concetto fosse intrinseco, indipendente cioè dal modo in cui la varietà è immersa in uno spazio affine. Un punto è non singolare, dimostrò Zariski, se, e soltanto se, la dimensione dell'anello locale OP in P è uguale alla dimensione del quoziente mP/(mP)2.
Un altro matematico che si convertì alla geometria algebrica negli anni Trenta del XX sec. fu il francese André Weil (1906-1998). Egli fu uno dei matematici di punta del gruppo Bourbaki, che in quegli anni si era posto l'obiettivo di redigere un manuale di analisi che fosse utile oltre che rigoroso. Un manuale che diventò un'enciclopedia: già dopo la Seconda guerra mondiale era un'opera in molti volumi. A tempo debito la redazione passò alla generazione successiva, e l'opera continuò a crescere senza però mai raggiungere una trattazione completa; oggi, però, la spinta iniziale sembra essere ormai esaurita. Weil diede numerosi contributi a questo gruppo: non solo ne fu animatore (ne inventò il nome e scrisse molti articoli), ma vi riversò i suoi interessi matematici. Aveva cominciato con la teoria algebrica dei numeri, per poi dedicarsi alla geometria algebrica. Weil fu imprigionato in Francia dal febbraio al marzo del 1940 per le sue idee pacifiste; in prigione poté studiare la 'suggestiva', come egli stesso la definiva, opera L'analysis situs et la géométrie algébrique (1924) di Lefschetz. Rilasciato, partì per l'America dove per qualche tempo insegnò in una università che si è sempre rifiutato di nominare, per quanta difficoltà vi aveva avuto di dedicare un po' di tempo alla ricerca. Finalmente Hermann Weyl (1885-1955) gli venne in soccorso procurandogli un invito a San Paolo del Brasile, dove fu l'unico a seguire un corso di geometria algebrica; il docente era Zariski. Risultato di questi studi fu il volume Foundations of algebraic geometry del 1946.
Weil aveva già incontrato Zariski a Roma nel 1925-1926. Essi concordavano pienamente sul fatto che occorresse studiare la geometria algebrica in un ambito molto più generale di quanto fatto fino ad allora, passando dalle varietà complesse a varietà definite su un campo qualunque. Nel caso di Weil questa esigenza era legata ai suoi interessi nella teoria dei numeri, nella quale si era soliti considerare campi di vario tipo con le loro chiusure algebriche. Tuttavia pur essendo d'accordo sugli scopi e pur avendo gli stessi standard, molto elevati, questi due matematici avevano differenti orientamenti. Weil pensava quasi certamente a Zariski quando scrisse queste parole (in un passo tanto più toccante se si pensa alle circostanze nel quale fu scritto):
Per quanto grati dobbiamo essere, noi geometri algebrici, alla moderna scuola di algebra per averci temporaneamente ospitato in costruzioni di fortuna piene di anelli, ideali e valutazioni e nelle quali alcuni di noi si sentono sempre in pericolo di perdersi, il nostro desiderio e il nostro scopo devono essere di ritornare nei palazzi che ci appartengono per diritto di nascita, per consolidarne le instabili fondamenta, provvedere ai tetti dove questi mancano, e portare a termine, in armonia con quanto già esiste, quanto è stato lasciato incompiuto.
Geometria algebrica e teoria algebrica dei numeri
L'influenza di Weil si è esercitata a lungo in molti campi; un punto tra i tanti è l'idea di considerare insieme geometria algebrica e teoria algebrica dei numeri. Discipline apparentemente separate per il fatto che le varietà sono definite su campi, mentre le questioni di teoria dei numeri riguardano gli anelli, in particolare l'anello degli interi, ma anche la loro estensione ad anelli di interi algebrici. Tentativi di sfruttare le analogie si erano però già avuti negli anni Ottanta del XIX sec., quando si cominciarono a studiare i legami tra gli ampliamenti algebrici degli interi e dei campi di funzioni.
Il progetto di Weil presentava tuttavia la novità di estendere a questioni aritmetiche le tecniche della coomologia che si pensava appartenessero soltanto alla geometria. Il problema che egli prese in considerazione era stato discusso in precedenza dai matematici tedeschi Emil Artin (1898-1962) e Helmut Hasse (1898-1979). Dato un polinomio in due o più variabili, è fondamentale sapere quante soluzioni intere possiede. Il semplice accorgimento, sfruttato per oltre un secolo, di considerare l'equazione modulo un numero primo p, permette spesso di concludere che non vi sono soluzioni intere. Per esempio, una soluzione intera dell'equazione x2=15y2+2 darebbe luogo a una soluzione intera modulo 3 della congruenza x2≡2 (mod3), ma è facile vedere che questa non ha soluzioni. D'altra parte può accadere che un'equazione dia luogo a molte congruenze modulo numeri primi che ammettono soluzioni, e gli studiosi di teoria dei numeri avevano cominciato a interessarsi al numero di queste soluzioni. Le motivazioni di Artin erano dovute a un'analogia che egli aveva scoperto con altre questioni di aritmetica. Fin dai tempi di Leonhard Euler (1707-1783) si sapeva che la funzione zeta:
[2] ζ(s)=∏(1-n-s)-1
permetteva di dimostrare risultati sui numeri primi. Un fatto che Riemann generalizzò trionfalmente nel lavoro sulla distribuzione dei primi. Il passo chiave iniziale consisteva nel considerare la funzione zeta come funzione della variabile complessa s. Sulla base del lavoro di Riemann, Jacques-Salomon Hadamard (1865-1963) e Charles de la Vallée-Poussin (1866-1962) dimostrarono, indipendentemente, il teorema dei numeri primi: esso afferma che il numero dei numeri primi minori di x tende asintoticamente a
Essi tuttavia non riuscirono a dimostrare l'ipotesi di Riemann secondo la quale gli zeri della funzione zeta, a parte quelli per valori interi negativi, si trovano tutti sulla retta s=1/2+it. Che la funzione abbia una certa simmetria rispetto alla retta Re(s)=1/2 segue facilmente da quella che si chiama 'equazione funzionale della funzione zeta', ma l'ipotesi di Riemann non è stata a tutt'oggi dimostrata. Se fosse vera, implicherebbe un gran numero di risultati sulla distribuzione dei primi, ed è quindi naturale che gli studiosi di teoria dei numeri abbiano dedicato molti sforzi per stabilirne la verità.
Nel 1924 Artin ebbe l'idea di introdurre la funzione zeta nel contesto dei polinomi in due variabili. Il modo più semplice di affrontare la questione è considerare la funzione zeta nel quadro generale tracciato dallo stesso Artin. Sia K un campo finito con q=pn elementi e K(t) un campo di funzioni su K. I polinomi sono gli interi razionali di questo campo. Vi è una stretta analogia tra K(t) e K[t] da una parte, e ℚ e ℤ dall'altra. Ai numeri primi di ℤ corrispondono polinomi irriducibili f in K[t]. La funzione zeta associata a K(t) si definisce come:
[4] ∏f(1-(qdegf)-s)-1
dove il prodotto è esteso a tutti i polinomi irriducibili f.
Artin affermò che questa funzione zeta soddisfa l'analogo dell'ipotesi di Riemann in una quarantina di casi semplici, anche se il caso generale sembra essere più difficile dell'ipotesi di Riemann originale. È un fatto notevole che questa supposizione si sia rivelata errata. Nel 1931 Friedrich Karl Schmidt (1901-1977) dimostrò servendosi del teorema di Riemann-Roch per le curve che la funzione zeta è razionale, essendo il rapporto di due polinomi a coefficienti interi. Queste funzioni sono particolarmente semplici, e Schmidt fu in grado di fornire l'espressione esplicita della funzione razionale e dimostrare che essa soddisfa una certa equazione funzionale. Artin aveva già congetturato che la funzione zeta deve soddisfare un'opportuna versione dell'ipotesi di Riemann. Come Hasse dimostrò più tardi, questa versione è equivalente alla seguente disuguaglianza:
[5] ∣Nn(q)-(qn+1)∣≤2gqn/2
dove Nn è il numero dei punti della curva le cui coordinate appartengono al campo Fq, q=pn e g è il genere della curva. Nel 1934 Hasse pubblicò due dimostrazioni della congettura nel caso del genere g=1 (curve ellittiche). Era chiaro che la prima avrebbe funzionato soltanto per queste curve. La seconda era più geometrica: considerava infatti le applicazioni della curva in sé, ed era possibile che funzionasse anche per curve di genere maggiore di 1.
Nel 1940 e nel 1941 Weil abbozzò due dimostrazioni del risultato generale per curve di genere qualunque. La prima considerava le corrispondenze della curva in sé, e quindi, con argomenti propri della teoria delle curve definite sui numeri complessi, calcolava il numero dei punti fissi in questa corrispondenza. La seconda si basava interamente sulla teoria delle corrispondenze di Severi per definire quella che chiamò 'funzione traccia'. Una proprietà cruciale di questa funzione fu stabilita applicando la disuguaglianza di Castelnuovo; una dimostrazione che era la generalizzazione cercata dell'argomento geometrico di Hasse.
All'argomento di Weil mancava però un fondamento rigoroso: i risultati fondamentali erano infatti stabiliti solo per il campo complesso ℂ e con metodi trascendenti. Per questa ragione Weil scrisse Foundations of algebraic geometry. Come abbiamo osservato in precedenza, in questo libro si generalizzano le tecniche di geometria algebrica per poter operare con campi non algebricamente chiusi. Su queste solide fondamenta egli poté quindi pubblicare dimostrazioni rigorose dell'ipotesi di Riemann sia per le curve sia per alcune classi particolari di varietà algebriche, le varietà abeliane. Nel 1949 Weil associò poi una funzione zeta a ogni varietà algebrica, formulando alcune precise congetture sulla funzione. Congetturò in particolare che dovesse trattarsi di una funzione razionale, di una forma tale che valga l'ipotesi di Riemann, e dovesse soddisfare una certa equazione funzionale. Inoltre, quando la varietà proviene da una varietà algebrica definita su ℂ, i coefficienti della funzione devono essere i numeri di Betti della corrispondente varietà complessa. Il motivo per formulare queste congetture sta nell'analogia che Weil supponeva esistesse con la formula di Lefschetz della topologia algebrica, che riguarda il numero di punti fissi di un'applicazione di una varietà in sé. Come commentò Nicholas M. Katz "alla ricerca di una 'teoria coomologica per varietà su campi finiti' che potesse giustificare questo argomento euristico si deve, direttamente o indirettamente, molta parte dell'enorme progresso della geometria algebrica negli ultimi venti anni".
Dopo un certo numero di tentativi senza successo, e dopo che Bernard Dwork aveva fornito un'inattesa dimostrazione della congettura sulla razionalità della funzione zeta, Alexander Grothendieck e Michel Artin (figlio di Emil) elaborarono un'opportuna teoria coomologica che permise loro di dimostrare che la funzione zeta è effettivamente razionale e che soddisfa l'equazione funzionale richiesta. La dimostrazione dell'ipotesi di Riemann per questa funzione doveva rivelarsi molto più difficile, e fu ottenuta infine da Pierre-René Deligne, un allievo di Grothendieck. Per questo risultato, nel 1974 Deligne ottenne la medaglia Fields.
Il teorema di Riemann-Roch
Il teorema di Riemann-Roch per le curve fu dapprima formulato come una disuguaglianza riguardante il numero di funzioni razionali indipendenti su una superficie di Riemann che hanno al più un numero fissato di poli. Successivamente fu generalizzato alle superfici complesse, e quindi alle varietà algebriche tridimensionali da studiosi come Severi in Italia e John A. Todd (1908-1994) in Inghilterra. Quasi subito dopo la fine della guerra alcuni matematici cercarono di generalizzare il teorema a varietà algebriche di dimensione qualunque. Il lavoro di Riemann era stato generalizzato a varietà complesse di dimensione qualunque da un matematico scozzese, William V.D. Hodge (1903-1975), nel libro The theory and applications of harmonic integrals (1941). Il problema consisteva nel fatto che una stretta relazione tra funzioni armoniche e funzioni analitiche esiste soltanto in dimensione 1. Hodge mostrò come costruire forme armoniche di periodo arbitrario, ossia, nella terminologia che Weil preferiva e che fu adottata in seguito da tutti, mostrò come trovare l'unica forma armonica che corrisponde a ogni dato elemento di un opportuno gruppo di coomologia.
Il lavoro di Hodge, anche se ammirevole, presentava però una lacuna, poi colmata da Weyl e Kunihiko Kodaira (1915-1997) durante la Seconda guerra mondiale. Dopo la guerra, Kodaira pubblicò il suo lavoro assieme alla generalizzazione del teorema di Riemann-Roch a varietà qualunque. Il successo ottenuto con la teoria delle forme armoniche lo spinse ad affrontare la teoria, più difficile, delle varietà algebriche complesse. Egli trattò dapprima il caso delle varietà complesse di dimensione 2, nelle quali il divisore è una curva priva di componenti irriducibili multiple; quindi nel 1952 il caso della dimensione 3, e solo successivamente il caso generale. Egli fu allora in grado di risolvere una congettura di Severi relativa alle diverse definizioni di genere che sono possibili per una varietà, e ciò facilitò il compito di stabilire quale forma avrebbe dovuto avere il teorema generale di Riemann-Roch. Un elemento essenziale in questo lavoro è la teoria dei fibrati lineari, che a sua volta era stata resa possibile dall'uso sistematico della teoria dei fasci, oggetto allora dell'opera pionieristica di Donald C. Spencer (1912-2001), americano e collega di Kodaira, e del giovane francese Jean-Pierre Serre.
I fasci erano stati introdotti da Jean Leray (1906-1998) solo alcuni anni prima. Serre e Henri Cartan dimostrarono per primi, negli anni 1950-1951, che si tratta di uno strumento naturale nello studio della teoria delle funzioni complesse su una varietà complessa. Grosso modo, e per fare soltanto un esempio, un fascio utile è quello dei germi delle funzioni olomorfe su una varietà complessa, che si ottiene considerando le funzioni olomorfe definite su aperti della varietà. Se f è una tale funzione, definita su un aperto U, e g e V rappresentano una coppia dello stesso tipo, allora le due coppie si dicono equivalenti se f e g coincidono sull'intersezione U∩V. Le classi di equivalenza di tali oggetti costituiscono il fascio dei germi delle funzioni olomorfe sulla varietà complessa. Altri fasci altrettanto facili da ottenere sono quelli dei germi di funzioni con particolari singolarità, e i fasci ottenuti considerando, invece delle funzioni, le sezioni di fibrati.
Un vecchio teorema di Cousin sull'esistenza di una funzione di più variabili che soddisfa certe condizioni doveva rivelarsi utile per indicare come tradurre vantaggiosamente queste questioni nel linguaggio coomologico. Un lavoro che spinse Serre a formulare una teoria delle forme complesse olomorfe e, in definitiva, un'altra versione del teorema di Riemann-Roch in dimensione superiore. Nel frattempo un giovane matematico tedesco, Friedrich Ernst Peter Hirzebruch, lavorava al recupero della grande tradizione matematica tedesca distrutta dal nazismo. Ispirandosi ai lavori di Hans Grauert, Reinhold Remmert, Karl Stein e altri, che avevano solo qualche anno più di lui, anche Hirzebruch formulò il teorema di Riemann-Roch per varietà complesse. Si basava su un precedente lavoro di Todd, che egli chiariva notevolmente formulando quello che chiamò il 'genere di Todd', un'espressione in termini dei dati puramente topologici della varietà complessa. Espresso in questo modo, il teorema di Riemann-Roch fornisce informazioni sull'esistenza di funzioni analitiche su una varietà complessa esclusivamente in termini della topologia della varietà. Un risultato veramente notevole.
Il teorema di Riemann-Roch determina la dimensione dello spazio di funzioni aventi determinate singolarità (su una curva, i poli). Il luogo dei punti singolari è generalmente una sottovarietà o una sottovarietà algebrica di codimensione 1, e come tale definisce un fascio lineare: il teorema di Riemann-Roch riguarda in modo naturale i fasci lineari, e ciò ne fa un argomento della teoria dei fibrati vettoriali. Nei primi anni Cinquanta del XX sec. questa teoria fu una delle tante riformulate da Grothendieck. Grazie al suo lavoro lo spazio di tutti i fibrati vettoriali su uno spazio X, che egli denotò con K(X), diventa un oggetto di studio di una grande ricchezza. Un fibrato vettoriale su X si può pensare come una famiglia di spazi vettoriali parametrizzata dallo spazio X. In particolare, per ogni punto x di X c'è uno spazio vettoriale Ex detto 'fibra'. Allo stesso modo in cui si forma la somma diretta di due spazi vettoriali, si può formare la somma diretta E1⊕E2 di due fibrati vettoriali su X, che ha come fibra su x semplicemente E1x⊕E2x. In modo analogo, il prodotto tensoriale di due spazi si generalizza nel prodotto tensoriale di due fibrati vettoriali, e queste due operazioni di somma e prodotto danno a K(X) la struttura di anello, graduato in modo naturale dal grado dei fibrati vettoriali che contiene.
Il fatto che K(X) possegga molte proprietà dell'usuale anello di coomologia di uno spazio suggerì a Grothendieck che la corrispondenza che associa a uno spazio X lo spazio K(X) assomigliasse molto a quella che associa a uno spazio il proprio gruppo di coomologia. Vista sotto questa luce la K-teoria appare come un nuovo tipo di teoria coomologica. La K-teoria di uno spazio diventò rapidamente un oggetto di interesse indipendente, stimolando la ricerca di altre teorie coomologiche. Ciò che invece essa suggerì a Grothendieck fu che il teorema di Riemann-Roch confrontava dati di due tipi, uno riguardante la varietà, l'altro un certo fibrato definito sulla varietà. Questi dati erano espressi sotto forma di due gruppi di coomologia. Di conseguenza, il miglior quadro generale per il teorema di Riemann-Roch risultava essere il confronto fra due coomologie.
A questo punto Grothendieck fu fortemente influenzato dai concetti della teoria delle categorie, formulata in origine da Saunders Mac Lane e Samuel Eilenberg (1913-1998), e applicata da Eilenberg e Norman Earl Steenrod (1910-1971) allo scopo di dare un senso alla confusa proliferazione di teorie coomologiche nel periodo 1930-1950. La teoria delle categorie era progredita fino ad acquisire una vita propria, ma Grothendieck fu il primo ad accorgersi che essa avrebbe potuto fornire un adeguato fondamento per la topologia algebrica e la geometria algebrica. Pensare in termini di categorie significa pensare a una classe di oggetti (per es., la classe di tutti gli spazi topologici, o quella di tutti gli anelli) assieme a una classe di opportune applicazioni tra queste (funzioni continue o rispettivamente omomorfismi di anelli). Una categoria è una di queste classi assieme alle relative applicazioni. Applicazioni tra due categorie, i 'funtori', associano oggetti di una categoria a oggetti dell'altra, e applicazioni ad applicazioni. Una teoria della topologia algebrica appare allora come un funtore che associa un anello a uno spazio topologico, e un omomorfismo di anelli a ogni funzione continua tra due spazi topologici. Tutto ciò portò Grothendieck a una straordinaria generalizzazione del teorema di Riemann-Roch, formulandolo come un teorema sulle applicazioni tra due spazi topologici. Il teorema di Riemann-Roch secondo Hirzebruch risulta un caso particolare, quello in cui lo spazio immagine è un punto. Incoraggiato dai successi in topologia algebrica, Grothendieck si rivolse con la sua eccezionale energia a questioni che hanno più direttamente a che fare con la geometria algebrica. Il risultato fu una nuova impostazione della disciplina e, non da ultimo, una riformulazione della teoria in termini realmente intrinseci.
Geometria algebrica intrinseca
Una delle più profonde intuizioni di Riemann fu che una curva complessa va studiata indipendentemente da ogni equazione che la definisce, e quindi da ogni immersione della curva nel piano o in uno spazio di dimensione superiore. L'intuizione era però così profonda che per lungo tempo fu respinta a vantaggio di metodi più algebrici che partono dall'equazione della curva. Mentre le idee di campo di funzioni e di divisori erano adeguate a formulare una teoria intrinseca delle curve, esse non lo sono, come si è visto sopra, nel caso delle superfici.
La teoria ispirata dalla Noether e sviluppata da van der Waerden, Krull e Zariski era una teoria degli ideali di polinomi, e dunque una teoria di varietà immerse in uno spazio affine o proiettivo. In questo quadro si cercò di ottenere risultati intrinseci, e fu possibile formulare una definizione astratta di varietà algebrica. Fu Weil, nei Foundations, a dare per primo questa definizione. La sua idea era di costruire un nuovo tipo di varietà, astratta, prendendo un insieme finito di varietà e un insieme compatibile di applicazioni birazionali tra di esse, per ottenere varietà jacobiane associate a curve (come Riemann aveva già fatto, ma Weil operò in un contesto più generale). In seguito Wei-Liang Chow dimostrò che tali varietà non erano in realtà oggetti più generali, ma Masahoshi Nagata provò che era possibile definire varietà nel modo indicato da Weil, che non fossero varietà proiettive.
La definizione di Weil seguiva in qualche modo quella di varietà che veniva allora introdotta in topologia. A Grothendieck non restava che andare fino in fondo sulla strada aperta dalla Noether e produrre una classe di varietà così generale che ogni anello corrisponde a una varietà.
Abbiamo visto che a ogni varietà affine corrisponde l'anello delle sue coordinate affini; è un anello privo di divisori dello zero, finitamente generato sul campo base K. Grothendieck fece il grande passo di partire da un anello commutativo qualunque e definire uno spazio topologico a esso associato. Generalizzò l'idea di anello delle funzioni regolari su una varietà affine in quella di un'intera famiglia di anelli definiti sullo spazio topologico. Dimostrò infine come mettere insieme questi oggetti per formare oggetti ancora più generali (come aveva fatto Weyl per le varietà astratte). L'oggetto risultante viene detto 'schema', e ogni anello si ottiene come anello delle sezioni di uno schema affine.
L'insigne matematico americano Robin Hartshorne ha scritto che l'introduzione degli schemi ha senza dubbio rivoluzionato la disciplina rendendo possibili enormi progressi. Tra questi si possono ricordare l'aver reso rigorose le intuizioni della scuola italiana, la risoluzione di numerosi problemi aperti e la crescita rigogliosa della disciplina. E non sorprende che il prezzo da pagare sia che occorra impadronirsi di una grande quantità di strumenti tecnici, e che alcune intuizioni sulle varietà non valgano più. Problemi questi che sono stati affrontati sfruttando la crescita notevole dell'algebra commutativa.
Grothendieck capì acutamente che la geometria algebrica era limitata a un ambito troppo ristretto, e che tutta la teoria doveva essere un dizionario che permettesse una traduzione tra spazi e anelli, e fino a un certo punto lo era. Tuttavia per Grothendieck gli spazi non erano definiti in modo adeguato, e gli anelli allora considerati non potevano avere elementi nilpotenti (un elemento è nilpotente se non è zero, ma una sua potenza è zero).
Nonostante i tecnicismi che vi intervengono, possiamo dare un'idea dell'utilità di allargare l'ambito della geometria algebrica includendo gli anelli con elementi nilpotenti. Un teorema della teoria dei sistemi non lineari di curve ha svolto un ruolo centrale nell'estensione del teorema di Abel al caso bidimensionale. Le curve di questa famiglia si possono pensare tutte come deformazioni di una di esse. Il teorema in questione fu dimostrato la prima volta da Enriques, e poi indipendentemente da Poincaré con metodi di analisi complessa. Vi furono però presto perplessità a proposito della dimostrazione di Enriques, e quando i geometri algebrici cominciarono a considerare la geometria su campi qualunque, le residue preoccupazioni si trasformarono apertamente in dubbi, e si dimostrò che il teorema, nel modo in cui era enunciato, era falso in caratteristica p. Tuttavia, con grande sorpresa di tutti, risultò che, come conseguenza del lavoro di Grothendieck, era possibile fornire condizioni necessarie e sufficienti per la validità del teorema, e che inoltre una dimostrazione puramente algebrica era a portata di mano.
I progressi ottenuti erano dovuti principalmente all'uso sistematico degli elementi nilpotenti. Questi compaiono in relazione a famiglie di curve di una superficie su uno spazio di parametri con un solo punto, ma con un fascio a struttura nilpotente non banale, ovvero, in termini geometrici, quando in alcuni casi particolari occorre considerare deformazioni di ordine superiore delle curve.
In una serie di straordinari lavori per il Séminaire Bourbaki, e poi nel corso di due lunghe serie di seminari, Grothendieck sviluppò una visione completamente nuova della geometria algebrica. Essa si basava saldamente sulla teoria delle categorie che forniva il quadro concettuale entro il quale certi problemi, estremamente difficili, potevano essere considerati in un certo senso problemi tecnici. Gli oggetti centrali di questa teoria sono gli schemi: ogni varietà algebrica genera immediatamente uno schema, ma non tutti gli schemi provengono dalle varietà. Tra gli schemi vengono definiti diversi tipi di morfismi, e con qualche difficoltà si possono costruire un certo numero di coomologie diverse. Il risultato è una teoria molto sofisticata e potente, e a chi voglia cominciare dall'inizio ad addentrarsi nello studio di questa teoria, essa si mostrerebbe in tutta la sua eleganza e naturalezza. Essa si deve a una notevole parte dei migliori giovani matematici francesi e, grazie a David B. Mumford, anche a molti matematici americani. Il successo del loro lavoro, che forse per la prima volta forniva una teoria della geometria algebrica in un quadro generale che poteva rivaleggiare con le teorie della topologia algebrica, stimolò altri ricercatori, e gli schemi divennero il punto di partenza di tutte le teorie moderne.
Come si è visto in precedenza, uno dei risultati di questo lavoro fu la risoluzione di tutte le congetture di Weil. Un successo al quale contribuirono in molti, specialmente Grothendieck, e, nei primi anni Settanta del XX sec., Deligne. È notevole che a quel punto Grothendieck avesse già abbandonato il suo programma, anche prima di aver messo per iscritto in modo rigoroso i molti nuovi teoremi. Spinto dapprima dai movimenti pacifisti della fine degli anni Sessanta del XX sec., e quindi da altre idee sul suo ruolo come matematico in una società nella quale si sentiva sempre più a disagio, abbandonò per qualche tempo gli studi matematici. Si mise anche a criticare il lavoro di coloro che invece erano rimasti per finire quanto lui aveva cominciato, e non soltanto per gli aspetti tecnici ma a volte anche per il modo in cui il lavoro veniva svolto. Una polemica infelice echeggiò per qualche tempo negli anni Ottanta del secolo scorso: si può supporre che sarà uno dei compiti degli storici stabilire un'accurata attribuzione di paternità dei risultati raggiunti.
Uno dei più acuti sostenitori della nuova impostazione fu Mumford. Egli univa una grande abilità di tecnica matematica con la capacità di fornire motivazioni mediante numerosi esempi che convinsero molti matematici americani ad abbracciare la nuova teoria. Essendo stato allievo e amico di Zariski era un esperto delle teorie classiche, ma divenne subito un maestro delle idee di Grothendieck.
Uno degli argomenti ai quali si dedicò con successo fu quello degli spazi di moduli, un argomento ancora oscuro all'epoca (un altro argomento le cui origini si trovano nell'opera di Riemann). In Geometric invariant theory (1965) Mumford fa rivivere la teoria degli invarianti del XIX sec., e inquadrandola nella nuova teoria degli schemi costruisce una teoria rigorosa e di ampio respiro. La distinzione che egli fa tra oggetti in grado di fornire spazi di moduli trattabili e quelli che invece non lo sono è molto potente; i primi li definì 'stabili'. Per i suoi lavori sugli spazi di moduli e su molti altri argomenti di geometria algebrica Mumford fu insignito della medaglia Fields nel 1974.
La ricerca in geometria algebrica è oggi molto attiva. La recente classificazione di Shigefumi Mori delle 3-varietà algebriche, che utilizza il lavoro di molti matematici di tutto il mondo e gli è valsa l'attribuzione della medaglia Fields nel 1990, completa una naturale linea di ricerca cominciata dai matematici italiani all'inizio del XX secolo. Esiste oggi una fiorente ricerca che ha lo scopo di approfondire i legami tra geometria algebrica e teoria dei numeri algebrici. Molti importanti problemi sono stati risolti con questa impostazione. Un grande successo è stata la conferma da parte di Gerd Faltings nei primi anni Ottanta del XX sec. della congettura di Louis J. Mordell (1888-1972), secondo il quale vi sono soltanto un numero finito di punti razionali su una curva di genere maggiore di 1. Il lavoro di Faltings, basandosi su precedenti risultati della scuola russa, in particolare di Aleksej Nikolaevič Paršin e S. Arakelov, fa derivare la congettura di Mordell da altre congetture, apparentemente più profonde, delle teorie moderne dei numeri algebrici e della geometria algebrica. Ciò ha incoraggiato i matematici a proseguire su questa strada, e Andrew J. Wiles nel 1996 riuscì a dimostrare una delle più famose e popolari congetture della matematica: l'ultimo teorema di Fermat.
© Istituto della Enciclopedia Italiana - Riproduzione riservata