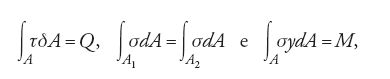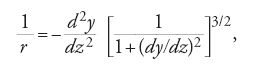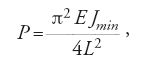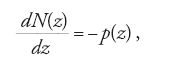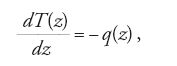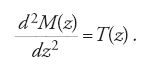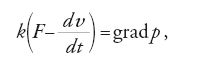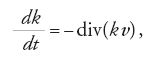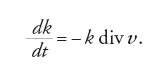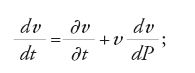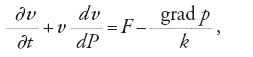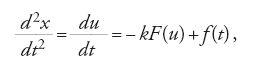L'Età dei Lumi: matematica. Meccanica e ingegneria
Storia della Scienza (2002)
L'Eta dei Lumi: matematica. Meccanica e ingegneria
Meccanica e ingegneria
Alla fine del XVII sec. e forse anche agli inizi di quello successivo, prima della formalizzazione del calcolo differenziale da parte di Leibniz, la matematica viveva ancora la grande stagione del 'calcolo geometrico'; nella meccanica il formalismo algebrico, sino ad allora utilizzato, era ancora vincolato a una sua traslitterazione in termini geometrici. La geometria era lo strumento che dava senso alle formule usate nei diversi campi del sapere meccanico; essa era in grado di dominare l'immaginario degli scienziati e di condurli per mano lungo le complesse vie del ragionamento fisico.
Quando Galilei pubblica a Leida i Discorsi e dimostrazioni matematiche intorno a due nuove scienze attenenti alla mecanica et i movimenti locali (1638), aprendo una nuova stagione per le scienze meccaniche e inaugurando, di fatto, una nuova disciplina, la 'scienza delle costruzioni', la geometria rappresenta lo strumento principe che guida Salviati, uno dei tre personaggi dei dialoghi, alla scoperta da parte dei suoi interlocutori Sagredo e Simplicio della "nuova scienza". La geometria è la disciplina che Galilei usa con sapienza e grande perizia, anche se i suoi ragionamenti a una prima sommaria lettura appaiono complessi e, in alcuni casi, alquanto contorti; essa, tuttavia, è il linguaggio attraverso il quale lo scienziato pisano spiega le sue acute e innovative intuizioni sulla resistenza dei materiali, le sue considerazioni sulla "Scientia nuova altra, de i movimenti locali", quelle sul moto dei proietti e altro ancora.
Per tutto il Rinascimento i fondamenti della meccanica, a partire da quella antica di origine aristotelica per proseguire con quella medievale di Giordano Nemorario (XIII sec.), e in seguito con quella di Simon Stevin (1548-1620) e di Gilles Personne de Roberval (1602-1675), avevano visto convivere, in un ingarbugliato intreccio, principî meccanici e regole empiriche, numeri e grandezze, algebra e geometria. Le 'scienze meccaniche' erano rimaste orientate alla costruzione di macchine da cantiere e di macchine idrauliche, trascurando un approfondimento della disciplina sul piano teorico, come era avvenuto per i 'precetti' dell''Arte e della Scienza del costruire', propri della tradizione costruttiva antica e medievale; esse si erano dipanate come una matassa in un labirinto, senza un percorso predefinito, ordinato e chiaro. Gli strumenti interpretativi dei principî meccanici utilizzati dagli scienziati erano le macchine semplici: la leva, la bilancia e la stadera, il piano inclinato, la carrucola, il cuneo, la vite. Strumenti semplici che, tuttavia, opportunamente usati, erano stati in grado di aprire uno spiraglio sui fondamenti della statica (la scienza dei pesi) e, più in generale, su quelli della meccanica, sulla gravità (gravitas secundum situm), sul moto e così via. L'autorità della geometria euclidea e la coerenza della statica archimedea erano al tempo stesso garanzia e sicurezza dei principî usati nelle arti meccaniche.
Tali premesse portarono a un incedere lento dei progressi scientifici in questo importante settore del sapere, sino a quando, agli inizi del XVII sec., la "fantasia geometrica di Kepler e la spregiudicatezza aritmetica di Wallis" (Bottazzini 1990, p. 4) stimolarono gli studiosi a elaborare nuovi e autonomi percorsi teoretici di ricerca, svincolandosi dall'attenta e ossequiosa osservanza delle opere degli antichi. L'accelerazione fu sempre più rapida, in concomitanza con la diffusione sempre maggiore dei nuovi strumenti formali del calcolo differenziale e integrale e del calcolo delle variazioni. Questi strumenti matematici innovativi configurarono così un nuovo percorso scientifico, ma anche linguistico, che interessò la teoria delle proporzioni e la geometria euclidea, il calcolo isoperimetrico e quello differenziale, giungendo a rivoluzionare, nel breve arco di circa un secolo e mezzo, i metodi d'interpretazione dei principî statici e meccanici. L'orizzonte della ricerca cambiò; lo studio degli autori antichi non fu più visto come strumento di confronto delle nuove scoperte con un insieme di conoscenze consolidate e accettate da secoli di tradizione, ma cambiarono gli scenari e l'obiettivo divenne quello di andare oltre in ogni campo del sapere con nuovi strumenti, nuovi metodi di calcolo, nuovi linguaggi. Da questo punto di vista, Descartes aprì la via a una radicale riforma concettuale del rapporto tradizionale tra algebra e geometria, inaugurando una nuova stagione per la matematica che avrà non poca influenza sugli sviluppi della meccanica. L'invenzione del calcolo differenziale da parte di Leibniz e Newton, finalizzata, in senso leibniziano, a una matematizzazione della scienza o a una mathesis universalis, mutò dunque scenari e prospettive di ricerca. L'ambizioso progetto di Leibniz era, infatti, quello di ridurre la meccanica a pura geometria per mezzo di un solo assioma metafisico. Il calcolo delle quadrature, lo studio di una grande varietà di curve (cicloidi generalizzate, ovali di Descartes, curve logaritmiche ed esponenziali, ellissi, iperboli, ecc.), la rettificazione di un arco di curva o la determinazione della sua lunghezza, la ricerca delle tangenti, il calcolo del volume di un solido, la determinazione del baricentro di figure piane o tridimensionali erano tutti problemi che richiedevano nuovi strumenti matematici. Tali strumenti dovevano essere in grado di rappresentare, nell'ottica newtoniana, le linee in quanto generate "per moto continuo di punti", le superfici generate "per moto continuo di linee" e i volumi "per moto continuo di superfici", cosa peraltro osservabile in Natura ‒ come lo stesso Newton aveva fatto notare ‒ "ogni giorno nel movimento dei corpi". Si trattò dunque di una rivoluzione in senso fisico delle grandezze matematiche motivata dalle nuove idee di Newton sulle fluenti e sulle flussioni esposte nell'opera Methodus fluxionum et serierum infinitarum (1671), in cui egli anticipò quello che sarebbe divenuto il tema del nuovo calcolo infinitesimale.
Il grande scambio epistolare tra i matematici del Seicento fu uno dei veicoli di maggior diffusione dei nuovi metodi di calcolo e l'occasione per far emergere nuove questioni anche attraverso il confronto di differenti soluzioni per uno stesso problema, spesso accompagnate da vivaci querelles, polemiche e discussioni sulla correttezza o meno dei risultati conseguiti. Inoltre, questa diffusione di nuove idee e scoperte tra gli scienziati allargò soprattutto il campo d'azione dei matematici che uscirono dai loro ambiti strettamente disciplinari interessandosi di problemi meccanici come di resistenza dei materiali, di curve elastiche, di statica e di stabilità dell'equilibrio delle strutture, dimostrando vieppiù l'affermazione di quella "geometria più sublime" evocata da Leibniz già nel 1684.
Per rimanere in ambito strettamente meccanico, è dunque opportuno riassumere alcuni momenti significativi del turbinoso e travagliato periodo successivo alla pubblicazione dei Discorsi di Galilei. Nel 1678 Robert Hooke (1635-1703) pubblica a Londra la sua opera fondamentale Lectures de potentia restitutiva sull'elasticità. Nei fascicoli degli "Acta Eruditorum", pubblicati a Lipsia con il patrocinio del duca di Sassonia a partire dal 1684, compaiono importanti scritti di Leibniz, dei fratelli Bernoulli, Jakob I e Johann I, e di Guillaume-François-Antoine de L'Hôpital sullo studio delle curve algebriche piane. Jakob I Bernoulli (1654-1705) studia la spirale logaritmica e trova l'equazione della curva isocrona e della brachistocrona (la linea celerrimi descensus che corrisponde a una cicloide); lo stesso Jakob, con l'aiuto del fratello Johann I (1667-1748), risolve il problema della catenaria (di cui parleremo più approfonditamente in seguito) e pubblica l'equazione della lemniscata; Leibniz affronta il problema di trovare la curva inviluppo di una famiglia di curve date (problema equivalente all'integrazione di un'equazione alle derivate parziali); ancora Johann Bernoulli propone di determinare a quale specie di curva deve appartenere la curva di eguale pressione (o curva centrifuga). In tutti questi scritti viene alla luce la fecondità e l'efficienza apportata dal nuovo calcolo leibniziano nella risoluzione di delicati problemi di matematica e di meccanica, anche se alcuni studiosi, come, per esempio, Philippe de La Hire (1640-1718), raccomandavano vivamente l'uso della geometria ordinaria come strumento di verifica e garanzia dei risultati ottenuti con l'ausilio dei nuovi strumenti matematici.
Tuttavia, questa posizione metodologica non fu esente da critiche da parte dello stesso Leibniz, in quanto essa prevedeva l'uso di strumenti di calcolo à la façon des Anciens. Nel 1736 Leonhard Euler ‒ elogiato come princeps mathematicorum dal suo maestro Johann I Bernoulli ‒ pubblica la Mechanica sive motus scientia analytice exposita, dove espone un insieme di risposte a numerosi quesiti posti dallo studio della meccanica. In quest'opera si può intravedere un vasto e importante programma di ricerca al quale lo stesso Euler darà un grande contributo in una Opera omnia sviluppata in ben 88 volumi.
Nel 1744 lo stesso Euler dà alle stampe lo scritto Methodus inveniendi lineas curvas maximi minimive proprietate gaudentes, importante compendio di studi sul calcolo delle variazioni e sulle curve elastiche. Trent'anni dopo, nel 1773, Charles-Augustin Coulomb (1736-1806) scrive il suo Essai sur une application des règles de maximis et de minimis à quelques problèmes de statique, relatifs à l'architecture (1776) in cui chiarisce numerosi e importanti problemi attinenti alla scienza delle costruzioni, o meglio lo studio di alcuni problemi di statica relativi all'architettura ‒ come ha lasciato scritto nel titolo della sua opera ‒ quali la flessione dei prismi, la rottura dei solidi, la statica degli archi e delle volte, la teoria dei muri di sostegno, e altro ancora. Questo insieme di scritti ‒ compresi quelli che, per brevità, non abbiamo citato ‒ è il preludio sia alla rivoluzione scientifica in senso 'elasticista' che avverrà, nel XIX sec., nelle scienze meccaniche e in particolare nella meccanica dei solidi e delle strutture, a opera di Claude-Louis-Marie-Henri Navier, Siméon-Denis Poisson, Augustin-Louis Cauchy, George Green, Adhémar-Jean-Claude Barré de Saint-Venant, Alberto Castigliano, William Thomson, e altri ancora, sia al repentino risveglio di questo secolo su nuove complessità, nuovi strumenti, nuove tecniche d'indagine tese però più alla conoscenza 'assoluta' e completa di un particolare microcosmo scientifico che alla comprensione del macrocosmo dei saperi meccanici.
L'applicazione del calcolo differenziale e integrale alle scienze meccaniche
Il mutamento di scenario cui è stato fatto cenno nell'introduzione cambia gli obiettivi delle indagini speculative e lascia intravedere nuovi e sterminati campi di ricerca. Le questioni più strettamente legate alla costruzione delle macchine sono ormai risolte e lasciate ai tecnici piuttosto che agli scienziati; la pratica costruttiva indugia più sulle applicazioni concrete che sulle questioni teoriche, conducendo infinite indagini minute su questioni di tecnica, di tecnologia e sulla costruzione, e rinunciando, di fatto, a una visione più generale dei problemi. Le speculazioni teoretiche e il sapere scientifico cambiano palcoscenico e iniziano a essere esercitati nei circoli scientifici e nelle accademie, e a occuparsi di questioni più strettamente matematiche, dove la visione astratta del problema supera la questione più squisitamente 'meccanicistica' e dove l'accadere, sia quello fisico sia quello più 'spirituale', non è più governato dalla presenza di un ente superiore, ma assume il carattere di un qualcosa prodotto da una pura causalità meccanica e dunque non preordinato a una finalità superiore.
La scienza meccanica diventa in tal modo una disciplina che richiede l'uso del calcolo matematico per descrivere i suoi complessi fenomeni, e auspica l'introduzione di strumenti d'analisi di validità generale, in grado d'illustrare sia i fondamenti meccanici dei fenomeni fisici, sia le regole dei sistemi costruttivi. Dunque, non è più sufficiente dedurre le regole, così come i principî, attraverso una reductio all'uso di macchine semplici, per le quali è sufficiente conoscere l'algebra elementare e la sola geometria. Occorrono invece nuovi strumenti d'indagine più raffinati che consentano di abbracciare la generalità dei problemi per poi passare, attraverso le applicazioni, alla soluzione e all'esame delle numerose questioni meccaniche sollevate dalla matematica stessa. Si configura in questa maniera un percorso decisamente più 'razionale' e più 'scientifico' che va oltre la 'sapienza' dell'antico costruttore, la quale, con il solo uso dell'algebra e della geometria euclidea era stata, sino a tutto il Seicento, e forse in parte anche nel secolo successivo, la guida e l'anima, la ratio e la logica per costruire "macchine a vastità immensa" e per "fabbricar navilii, palazzi o templi vastissimi".
Come aveva sostenuto l'abate Francesco Maria Franceschinis della Valle (1761-1835) nel 1807, in occasione dell'orazione inaugurale dell'anno accademico dell'Università di Padova, nelle arti e nelle tecniche non si sarebbe potuto conseguire nulla di bello e di utile se non attraverso la cooperazione di due "nobilissime sorelle": la matematica e l'esperienza empirica. L'incontro di queste due discipline metteva in luce ‒ a suo avviso ‒ il ruolo svolto dalla meccanica, dedita allo studio del moto e dell'equilibrio, nello sviluppo del pensiero scientifico: essa, infatti, conserva il rigore e la potenza astratta della matematica, ma sa anche aprirsi al riconoscimento e all'esplicazione dei fenomeni fisici.
Il progetto di Franceschinis raccoglieva in sé la tradizione aristotelica della scienza del moto, la concezione di Archimede, orientata alla fondazione assiomatico-deduttiva della statica, e tutti i successivi tentativi degli scienziati rinascimentali di edificare la meccanica come scienza subalterna alla sola geometria. Inoltre, esso conteneva già le ipotesi meccanicistiche per spiegare il 'sistema del mondo' e il dibattito settecentesco sulla natura razionale e non solamente empirica dei principî meccanici, sino a presagire il maturo disegno d'includere la meccanica nell'analisi matematica, concepito da Joseph-Louis Lagrange (1736-1813), nelle cui mani la meccanica era venuta a "raccogliersi in una sola formula" (Delle matematiche applicate, 1808, p. 73), in una suprema sintesi impreziosita da una sconfinata ricchezza di applicazioni.
Tuttavia, per comprendere il senso di questo importante progetto occorre fare alcune riflessioni sulla nascita dei principî e sugli sviluppi degli strumenti matematici che, a partire dal XVII sec., hanno mutato il paradigma e il linguaggio delle scienze meccaniche. Già Galilei nei Discorsi, e prima ancora nel Saggiatore nel quale con bilancia esquisita e giusta si ponderano le cose contenute nella Libra astronomica e filosofica (1623), aveva messo in luce un modo diverso di affrontare i problemi meccanici attraverso la sostituzione delle speculazioni metafisico-materialistiche con considerazioni di carattere più matematico, e rivedendo il principio secondo il quale tutto quello che sino allora era stato scoperto nella statica o nella meccanica non poteva essere il risultato della sola esperienza. Non è vero ‒ aveva fatto notare Galilei ‒ che si deve assegnare all'esperienza il primato sulla conoscenza e sulla speculazione scientifica, perché l'esperienza mostra che qualcosa accade, ma non basta a precisare cosa accada e in quale modo. Tuttavia, lo stesso Galilei aveva rimarcato che una teoria che si scontra con i dati dell'esperienza deve essere rifiutata poiché "anche un sol contrasto con l'esperienza è decisiva prova di falsità della teoria", ed era altrettanto convinto che ciò che dà sensatezza all'esperienza è la sua immediata traduzione matematica. Ecco dunque che la 'sensata esperienza', resa aderente al linguaggio matematico della Natura, è la prova reale, anzi la verità di ogni discorso; non è l'esperienza in sé, ma la 'sensata esperienza' che contribuisce a rivelare la realtà delle cose, aprendo così la via all'incedere di una 'nuova scienza'.
Nel Settecento si è assistito allora, sulla strada tracciata da Galilei, all'esplicita e inconfutabile preminenza assegnata nella speculazione scientifica alla matematica, che ne diviene strumento indispensabile ed esclusivo; la matematica, nelle nuove forme in cui si è sviluppata, soddisfa perfettamente le esigenze della ricerca ed è, com'era stata per Galilei la geometria, il vero strumento che apre il pensiero alla conoscenza del mondo.
Si viene così a delineare una nuova visione epistemologica della realtà, in cui il dato dell'esperienza non è più reso sensato dall'antica logica che lo inseriva in un grande sistema metafisico e fisico della realtà, ma riceve la sua sensatezza dalla formulazione di ipotesi matematiche che l'esperienza stessa è chiamata a convalidare. Il 'postulato' deve essere matematicamente fruibile, così da poter provare nuove proposizioni da sottoporre al controllo dell'esperienza. L'hypothetice diventa allora il paradigma fondamentale della scienza, la quale possiede in sé stessa il criterio per decidere sulla validità dei principî da essa stessa enunciati. La conseguenza di questa nuova impostazione concettuale dello studio dei fenomeni meccanici assegna alla matematica, come era stato in passato per la geometria, il primato sulla logica, con l'intento di andare oltre l'uso delle regole, diventate soltanto passaggi intermedi di una grandiosa dimostrazione matematica orientata a stabilire la meccanica come scienza rigorosa, razionale e formalmente distinta dalla geometria stessa. La costruzione di modelli matematici non si deve mai arrendere di fronte alla complessità dei fenomeni studiati, ma deve sempre tentare di rendere ragione dei principî, dei teoremi, degli scoli enunciati mediante l'introduzione di opportuni assiomi d'ordine generale che siano in grado di esprimere la natura del problema meccanico. La scelta di un modello semplice per rappresentare un problema meccanico, dotato del minor numero possibile di connotati o di proprietà fenomenologiche dell'oggetto fisico, garantisce allora esattezza geometrica alle proporzioni delle diverse parti che lo compongono. Tale modello può condurre alla definizione di un limite inferiore che ne caratterizza, per esempio, la resistenza ‒ come nel caso dei solidi galileiani, che, pur essendo figure della geometria euclidea, sono caratterizzati dalla proprietà di essere dotati di peso ‒ o ne descrive la curva ottimale in funzione di alcuni parametri ‒ per esempio, l'essere pesante, flessibile, estensibile o inestensibile ‒ che condizionano il problema.
Le proprietà dell'essere materiale caratterizzano dunque i problemi propriamente meccanici rispetto a quelli strettamente matematici e si differenziano da questi ultimi negli scopi e nelle finalità della ricerca delle soluzioni. L'obiettivo della speculazione scientifica è allora anche quello di circoscrivere il campo d'indagine e liberarlo della zavorra d'inconcludenti diatribe metafisiche. In questo senso, diventa necessario sospendere il giudizio su quelle questioni che si rivelano incerte dal punto di vista epistemologico, poiché eccedono i limiti della conoscenza umana o necessitano di nuovi strumenti interpretativi. Questa visione puramente matematica del mondo, che ebbe grande sviluppo a partire dalla fine del Seicento, non fu esente da feroci critiche, come quelle espresse su di essa dallo stesso Leibniz che pure contribuì al suo sviluppo: "I semplici Matematici, Filosofi a nozioni incomplete [Philosophes à notions incomplètes], che non s'occupano che dei giochi dell'Immaginazione, sono capaci di crearsi tali nozioni; ma esse sono distrutte da Ragioni superiori" (Recueil de diverses pièces sur la philosophie, la religion naturelle, l'histoire, les mathématiques, ed. 1740, p. 99). Tuttavia, proprio le notions incomplètes che caratterizzano secondo Leibniz alcuni matematici, riescono molte volte a descrivere problemi scientificamente fecondi e si rivelano capaci di coordinare un vasto insieme di fenomeni sotto leggi matematiche uniformi, complete e addirittura, in certi casi, suggestive per la loro formulazione. Alla vera causa fisica, forse destinata a rimanere per sempre nascosta nei segreti della Natura ‒ si pensi, per esempio, alla disquisitio intorno all'esistenza del vuoto ‒ si sostituisce un modello matematico il cui scopo non è la spiegazione del fatto reale, ma la sua rappresentazione. In questo senso, l'atto del rappresentare, soprattutto quando consente di prevedere grazie a un modello aspetti ancora ignoti della realtà, può diventare spiegazione in senso causale. Allora, "la causa deve appartenere al reale, altrimenti è inganno, mentre il modello si accontenta di appartenere al più vago orizzonte del possibile, e anzi a quello della sua limpida regione che è governata soltanto da prefissati principî matematici" (Benvenuto 1995, p. 255).
Si assiste così, relativamente all'esigenza della spiegazione causale dei fenomeni, a un rovesciamento dei termini del problema: il modello non rivela il perché, ma può essere accolto come se lo facesse. In questo senso, alle notions incomplètes richiamate da Leibniz resta il compito della chiarezza e della coerenza, requisiti che consentono la traduzione di queste nozioni in una veste matematica rigorosa. In questo modo il rigore del modello matematico sarà il mezzo per individuare il principio altrimenti cercato a partire dalle "Ragioni superiori" impigliate nella metafisica; esso costituirà a cavallo tra il XVII e il XVIII sec. uno dei temi ricorrenti nella ricerca matematica sulla scienza del moto, mentre nel XIX sec. sarà il perno attorno al quale ruoterà la diatriba sulla teoria matematica dell'elasticità tra Saint-Venant e Castigliano da una parte, e Green e Thomson dall'altra. A titolo di esempio, si può osservare che l'attrazione intermolecolare descritta da Newton, derivante da un'azione a distanza tra le particelle che spiega la forza di coesione che le tiene unite tra loro è, come l'ha definita Saint-Venant, "una legge sufficientemente generale, tanto 'grandiosa', quanto semplice perché noi possiamo considerarla come quella alla quale il sovrano Legislatore ha sottoposto i fenomeni intimi" (Note du § 11 à la Théorie de l'élasticité des corps solides de Clebsch, 1883, p. 41).
Il progetto di fondare la meccanica come rigorosa scienza razionale distinta dalla geometria si svilupperà alla fine del XVIII sec., anche con l'intento di risolvere la questione, ancora aperta, se sia lecito assimilare i principî matematici ai principî della Natura. Verso la fine del Settecento e i primi decenni dell'Ottocento, infatti, gli sviluppi del dibattito scientifico sulla resistenza dei materiali, sulle curve elastiche e flessibili, sul comportamento materiale che caratterizza la meccanica dei solidi e delle strutture, nonché il successivo ingresso della teoria assiomatica dell'elasticità, evidenziano ulteriormente l'attualità degli obiettivi della ricerca galileiana. L'analisi delle cause attraverso le quali è possibile spiegare la resistenza dei materiali e consentire altresì una descrizione generale e metafisica della deformazione dei corpi sotto sforzo, la definizione di modelli fisico-matematici atti a rappresentare in modo semplice e chiaro le modalità secondo le quali un solido o una struttura si deforma e si rompe sotto l'azione delle forze esterne, la necessità di chiarire le modalità secondo le quali un corpo si muove in un mezzo resistente o in un fluido: l'insieme di questi obiettivi evidenzia quel grande progetto scientifico che va sotto il nome di 'scienza degli ingegneri'. Questa racchiude in sé la totalità delle scienze meccaniche, vale a dire la meccanica dei solidi e delle strutture, la meccanica dei materiali, l'architettura statica e idraulica, la scienza del moto e la balistica, e altro ancora, ossia un insieme di 'saperi' finalmente liberato dalle diatribe metafisiche e in questa nuova veste più orientato alla conoscenza del mondo fisico reale.
I principali temi di meccanica del Settecento
Nel 1716 Jacob Hermann (1678-1733) pubblica ad Amsterdam un importante trattato sulla statica dei corpi rigidi, che comprende anche lo studio del moto isocrono dei corpi e la teoria dell'urto, nonché il problema dell'equilibrio e del moto dei fluidi, in cui fa largo uso del calcolo differenziale e anticipa i temi che saranno oggetto della rivoluzione matematica nella meccanica.
Alcuni anni dopo, Euler affronta la dinamica del punto materiale con l'intento di fondare una scienza razionale a partire dalla definizione di 'enti' primitivi: il punto materiale (corpus) e la forza (potentia), distinguendo tra quella 'assoluta', cioè la gravità che agisce sul corpo a prescindere dalle sue condizioni di moto, e quella 'relativa', il cui effetto dipende dalla velocità del corpo stesso. Euler introduce la legge fondamentale della dinamica, secondo la quale l'incremento della velocità dv di un corpo è proporzionale alla quantità pdt, dove p è la forza che agisce nell'intervallo di tempo dt. In questo modo Euler è in grado di studiare numerosi problemi relativi al moto di un punto materiale prescindendo dalla sua traiettoria (punto libero che si muove lungo una curva qualsiasi) e dal mezzo (un qualsiasi mezzo resistente o addirittura il vuoto).
Nel 1733 Daniel Bernoulli (1700-1782) stabilisce l'equazione differenziale che descrive l'oscillazione di un insieme di pesi sostenuti da un filo flessibile ‒ problema in seguito generalizzato da Euler al caso di una catena di pesi ‒, associando a questo tema la teoria delle corde vibranti già affrontata da suo padre Johann I e da Brook Taylor (1685-1731). L'argomento, di per sé stimolante, era stato preso in esame da Euler nel 1731 e i suoi studi lo avevano condotto alla definizione dell'equazione dell'oscillatore armonico. Nel 1740, Alexis-Claude Clairaut (1713-1765) propone a Euler di risolvere il problema dell'oscillazione di una massa fluida, riallacciandosi alla questione della definizione della forma della Terra. Il problema si può ricondurre, secondo il matematico francese, alla soluzione di un'equazione differenziale che descrive la condizione d'equilibrio di una forza generica ‒ in termini di componenti della forza rispetto a un sistema di riferimento cartesiano ortogonale ‒ che agisce su una particella del fluido. La condizione d'equilibrio cercata è quella che assegna alla massa fluida la forma di uno sferoide ellittico (tesi peraltro già sostenuta da Newton). Il fatto poi che la Terra sia appiattita ai poli, come dimostrato dalle ricerche sperimentali condotte in Lapponia per conto dell'Académie Royale des Sciences di Parigi, è una conseguenza ‒ secondo Clairaut ‒ della variazione di densità del nostro pianeta avvicinandosi dal centro della Terra alla superficie del globo.
La prima metà del XVIII sec. è una stagione ricca di contributi per lo sviluppo delle scienze meccaniche nel senso che abbiamo spiegato; nel 1736 appaiono il già citato trattato di Euler sulla meccanica e, su un versante più specifico, quello sul moto dei liquidi; due anni dopo, è dato alle stampe il trattato di Daniel Bernoulli sull'idrodinamica. E ancora, nel 1743, Jean-Baptiste Le Rond d'Alembert (1717-1783) pubblica il celeberrimo Traité de dynamique in cui espone il suo programma scientifico relativo alla scienza della meccanica, della quale si occuperà diffusamente negli anni seguenti. Ricordiamo, a questo proposito, i suoi contributi relativi alle equazioni cardinali dell'equilibrio di un corpo rigido, gli studi sul moto dei fluidi, sulla resistenza incontrata da un solido che si muove in un fluido (cosiddetto 'paradosso di d'Alembert'); quelli relativi al problema del moto di un grave, gli studi sulle vibrazioni trasversali di una corda elastica (studi che portarono alla formulazione dell'equazione di d'Alembert per le corde vibranti, nella forma di un'equazione alle derivate parziali del secondo ordine) e altro ancora. La tesi dello scienziato francese, che sottende al suo progetto scientifico, è la seguente: la meccanica è una scienza razionale, come la geometria e l'algebra, ed è fondata su principî necessariamente veri ed evidenti per sé stessi e non su ipotesi conseguenti a prove di carattere empirico. Si tratta di una rivoluzione metodologica che impone alla meccanica di espellere dal suo seno principî oscuri o non definiti, ipotesi inutili o sovrabbondanti; l'imperativo di d'Alembert è quindi ridurre i principî al minor numero possibile ma, allo stesso tempo, estenderne la generalità, affermando che essi sono tanto più fecondi, quanto più sono in piccolo numero.
A sostegno di questa tesi riportiamo il seguente esempio che meglio chiarisce il pensiero dello scienziato francese. In quegli anni era ormai consolidato presso i cultori di meccanica l'assioma secondo il quale la forza acceleratrice deve essere proporzionale alla causa che la genera, cioè ‒ secondo le ipotesi del tempo ‒ proporzionale alla velocità. D'Alembert aveva rimarcato che tale principio è inaccettabile come verità contingente perché ciò "rovinerebbe la certezza della meccanica e la ridurrebbe a non essere nulla più che una scienza sperimentale"; dunque tale principio, vero o falso che sia, "è inutile alla meccanica" e da essa deve essere bandito. Lo scienziato francese era però altrettanto critico nei confronti dei filosofi (nel caso specifico dei cartesiani), che accusava di perdersi in sottigliezze di carattere metafisico, e liquidò in modo altrettanto deciso la famosa querelle sulle forze vive, giudicata "di perfetta inutilità per la meccanica". Altre strade e altri principî dovevano essere cercati per fondare la meccanica su basi certe e razionali. Il principio dell'equilibrio, la definizione della forza d'inerzia e la composizione dei movimenti sono gli oggetti su cui, a parere del matematico francese, era necessario concentrare l'attenzione degli studiosi.
Secondo il programma di ricerca di d'Alembert, assegnato un sistema qualsiasi di corpi, ognuno dotato di un moto indipendente da quello degli altri, il problema generale della dinamica si riduce alla ricerca della legge che descrive il moto di ciascun corpo. Ciò lo condusse a formulare il principio della dinamica (noto come 'principio di d'Alembert') secondo il quale "durante un qualsiasi moto di un qualsiasi sistema materiale le forze perdute e le reazioni vincolari si fanno a ogni istante equilibrio". L'importanza di questo principio risiede nel fatto che ogni problema di dinamica può essere ricondotto a uno corrispondente di statica, nell'ambito della quale si considera semplicemente l'equilibrio tra le reazioni vincolari e le forze attive. Il successivo intervento di Lagrange, che ha saputo individuare la stretta connessione che esiste tra il principio di d'Alembert e il principio dei lavori virtuali, ha condotto nel modo più felice alla traduzione del principio di d'Alembert nelle equazioni di Lagrange, il più efficace strumento formale della dinamica.
Il programma di ricerca di d'Alembert aveva sollevato inoltre la seguente importante questione: se le leggi della statica e della meccanica siano leggi di verità necessaria o contingente. A questo proposito ricordiamo che in merito alla definizione di forza acceleratrice (φ) ‒ che secondo d'Alembert si può esprimere nella forma φdt=dv, dove dt è la variazione del tempo e dv quella della velocità ‒ erano state date diverse interpretazioni, orientate comunque a individuare nella definizione anzidetta un principio fondamentale della meccanica. Daniel Bernoulli aveva assegnato a questa definizione il carattere di verità contingente, mentre Euler, nella sua Mechanica, aveva tentato di dimostrare che si trattava di una verità necessaria. D'Alembert supera la questione assegnando alla forza acceleratrice il ruolo di quantità alla quale è proporzionale l'incremento di velocità, per cui è possibile ricondurre l'espressione della forza acceleratrice a una semplice definizione, che come tale deve essere trattata. Una prima conseguenza di questo suo diverso modo di affrontare la questione lo portò ad affermare che anche il principio di conservazione delle forze vive non è altro che una conseguenza delle leggi della dinamica e di quelle relative all'urto elastico dei corpi.
Un'impostazione metodologica di questo tipo diede luogo a diverse diatribe sui principî della meccanica, che videro scontrarsi tra loro personaggi del valore di Euler, Voltaire, d'Alembert e Maupertuis. In merito al problema della rifrazione della luce attraverso mezzi eterogenei, o a quello relativo all'urto elastico tra due corpi, Pierre-Louis Moreau de Maupertuis (1698-1759), che criticò aspramente la metafisica cartesiana, introdusse il principio di minima azione, secondo cui la Natura segue sempre la via più breve (o di "minor resistenza"), sottolineando però che questo principio era, a suo parere, solamente la conseguenza di un fatto puramente meccanico. Il principio di minima azione diventava allora per l'audace filosofo francese un principio di carattere generale, "regola e fondamento della sua concezione finalista dell'Universo e prova suprema dell'esistenza di un Essere onnipotente e onnisciente" (Bottazzini 1990, p. 41).
Euler, invece, più convinto che il principio di minima azione non fosse altro che un enunciato del calcolo delle variazioni, s'impegnò a darne una formulazione corretta dal punto di vista matematico, seppure limitata al caso di un punto materiale che si muove lungo una curva piana. La ricerca del minimo (o del massimo) della funzione che descrive il moto del punto lungo la curva assegnata riconduceva il problema, secondo Euler, nell'ambito della meccanica razionale e lo liberava da ogni 'principio metafisico'.
I primordi della teoria elastica della trave
Il modello del solido galileiano non trova più nel Settecento sufficiente autorità per restare al centro dell'attenzione degli studiosi. Nuovi oggetti e nuovi strumenti d'indagine richiedono un ulteriore approfondimento del problema della "resistenza dei corpi all'essere spezzati". Il modello del solido euclideo pesante non è più sufficiente per descrivere la realtà materiale dei corpi e dunque s'introducono nuovi parametri, per meglio descrivere tale comportamento materiale.
Nel 1678 Robert Hooke pubblica il suo testo fondamentale sull'elasticità, in cui espone i risultati delle ricerche da lui svolte sul comportamento elastico di una trave e, seppure sotto forma di anagramma, esprime la legge di proporzionalità (legge di Hooke) tra la forza F e lo spostamento elastico u, nella forma F=ku, dove k è una costante di proporzionalità. Johann I Bernoulli nel 1705 definisce la costante di proporzionalità come k=EA/L, in funzione di un nuovo parametro, il 'modulo di elasticità' E (o modulo di Young), e delle caratteristiche geometriche del solido, ossia la lunghezza L e l'area A della sua sezione trasversale. Il passaggio alla legge generalizzata di Hooke-Bernoulli in termini di tensioni σ=F/A e di deformazioni ε=ΔL/L è allora immediato e si compendia nella relazione σ=Eε.
L'introduzione dei concetti relativi all'elasticità e l'attenzione per il comportamento della trave durante la sua deformazione, piuttosto che lo studio del suo comportamento a rottura, attraggono l'attenzione degli studiosi e ampliano lo studio del 'problema di Galilei'. Edme Mariotte (1620 ca.-1684) estende il criterio di rottura di Galilei, basato sul concetto che la resistenza della trave dipende dal raggiungimento di una tensione limite (σ=σlim), osservando che esiste anche un limite all'elongazione delle fibre di cui è composta la trave e, tra queste, ne individua una 'neutra' che rimane indeformata; in questo modo introduce un criterio di rottura basato sulla deformazione limite (ε=εlim), ripreso nell'Ottocento da Adhémar-Jean-Claude Barré de Saint-Venant con il nome di 'criterio della dilatazione massima'. Leibniz nel 1684 estende ulteriormente il modello galileiano e, pur individuando in maniera erronea la posizione della fibra neutra, da lui collocata all'intradosso della trave semplicemente inflessa, determina la relazione che esiste tra la sollecitazione esterna, ossia il momento flettente M, e lo stato di tensione interno nella forma σ=(M/Ja)y, dove Ja è il momento d'inerzia calcolato rispetto alla posizione della fibra neutra e y è la posizione della generica fibra della trave. Occorre tuttavia sottolineare che a questa formula perverrà anche Pierre Varignon (1654-1722) nel 1702. Antoine Parent (1666-1716) formula finalmente l'equazione corretta, cercata ormai da tanto tempo, nella forma
[1] M=σmax BH2/6.
Si dovrà tuttavia attendere la fine del secolo per giungere a una chiarificazione del problema e alla sua soluzione definitiva, nella forma a noi oggi nota. L'artefice di questo risultato è Coulomb. Chiariti i dubbi sulla posizione della fibra neutra e individuato l'insieme delle componenti dello stato di tensione che agiscono sulla sezione trasversale della trave (una tensione normale σ e una tensione tangenziale τ), egli afferma che la soluzione si ottiene risolvendo un sistema di tre equazioni relative all'equilibrio del corpo, che sono note come 'equazioni cardinali della statica' e che esprimono l'equilibrio delle forze agenti secondo le direzioni normale e tangente al piano della sezione trasversale, e l'equazione di equilibrio alla rotazione; tali equazioni sono espresse nella forma
dove A è l'area della sezione trasversale, A1 e A2 sono rispettivamente la porzione di area soggetta a trazione e quella soggetta a compressione, Q è il peso esterno che agisce all'estremo libero della trave galileiana (nel caso specifico una trave a mensola) e M è il momento flettente generato dal peso Q e valutato rispetto alla generica sezione in corrispondenza della quale è calcolato l'equilibrio tra le forze esterne e le sollecitazioni interne.
Curve flessibili ed elastiche: il dibattito sull'equilibrio funicolare e l'equazione della catenaria
Uno tra i numerosi temi aperti dalla trattazione galileiana sulla resistenza della trave fu anche quello di determinare la posizione dell'asse della trave nella sua configurazione variata di equilibrio (o configurazione inflessa) sotto l'azione di un certo sistema di forze (carichi), ossia di determinare la sua 'linea elastica'. Era esperienza comune osservare che una verga o una lamina elastica sotto l'azione di un certo carico concentrato o distribuito s'incurva ‒ o, come più propriamente si dice, 's'inflette' ‒, anche se l'esempio della mensola galileiana, date le generose dimensioni della trave, consentiva poco di osservare il fenomeno; l'assunto anzidetto era invece evidenziato da un qualunque altro oggetto in cui una delle dimensioni del solido geometrico che lo rappresentava fosse preponderante sulle altre. Se nell'architettura tale problema interessava poco i costruttori e i maestri fabbricieri a causa delle cospicue dimensioni assegnate alle strutture portanti ‒ e anche perché, con riferimento ai problemi di ordine statico, l'interesse era più orientato a osservare la formazione delle lesioni e dunque la rottura dei corpi anziché lo stato di deformazione elastico ‒, dal punto di vista matematico il problema assumeva invece un'importanza particolare, che attrasse l'interesse di molti studiosi, soprattutto matematici, dalla fine del Seicento e per tutto il Settecento. I nuovi strumenti del calcolo infinitesimale e di quello variazionale trovarono in questo ambito un'adeguata palestra per cimentarsi ed esercitarsi, giungendo con Euler alla comprensione di un importante capitolo della meccanica, quello relativo alle curve flessibili ed elastiche.
Progenitore degli studi in questo contesto disciplinare fu il problema dell''equilibrio funicolare', cioè lo studio della configurazione, detta 'catenaria', assunta da una fune pesante fissata alle sue estremità. L'equazione della catenaria era già nota agli artisti rinascimentali; infatti, l'architetto Bartolomeo Ammannati se n'era servito per tracciare la forma dell'arco del ponte di Santa Trinita (1567) a Firenze. Il problema, in origine messo in luce da Galilei che aveva espresso l'opinione che la catenaria coincidesse con una parabola, attirò l'attenzione di numerosi studiosi. Isaac Beeckman alcuni anni prima di Galilei aveva risolto un problema simile, quello di una fune priva di peso e soggetta a un sistema di carichi uniformemente distribuito, ottenendo l'equazione di una parabola e trovando la soluzione al 'problema del ponte sospeso'. Questa stessa soluzione si trova in uno scritto del 1646 di Christiaan Huygens (1629-1695), che ribadì la differenza tra il problema del ponte sospeso e quello della catenaria, giungendo alla conclusione che, per quest'ultimo, la curva di equilibrio non poteva essere una parabola. Huygens formula un 'principio di estremo', secondo il quale la fune pesante assume quella posizione particolare per cui il suo centro di gravità nella configurazione di equilibrio è il più basso possibile; la soluzione non era ancora raggiunta, ma ciò sicuramente escludeva tra quelle possibili proprio la parabola. Nel 1673 il gesuita Ignace-Gaston Pardies (1636-1673) enuncia il suo teorema fondamentale per la catenaria, secondo il quale, qualunque sia la curva, il punto d'intersezione B tra due tangenti in due punti A e a appartenenti alla curva giace sulla verticale passante per il centro di gravità della porzione di fune sottostante alla corda Aa. Si tratta di un'intuizione geniale perché coincide con l'ipotesi che la fune possa essere sollecitata soltanto da una forza normale alla sua sezione trasversale; tale assunto verifica dunque l'equazione di equilibrio delle forze in gioco, che sono il peso della fune sottostante la corda Aa e gli sforzi agenti secondo le direzioni tangenti nei punti A e a. La conclusione alla quale giunse Pardies è la seguente: se la fune è omogenea e pesante, la curva cercata non può essere una parabola ed è pertanto la catenaria, mentre se la fune è priva di peso e su di essa agisce un'infinità di linee pesanti, parallele ed egualmente distanti tra loro, allora la fune assume un andamento parabolico. Infatti, il baricentro E del sistema di linee pesanti comprese tra il punto a e il punto medio F della corda aA passa anche per il punto medio (D) del segmento aB; a sostegno della sua tesi Pardies ribadisce che la parabola è l'unica curva per la quale le tangenti in a e nel punto di minimo (o massimo) della porzione di fune compresa nell'intervallo aA s'incontrano in un punto passante per la verticale tracciata per E. La discussione divampò quando Jakob I Bernoulli propose il tema all'attenzione degli scienziati del tempo con una memoria pubblicata negli "Acta Eruditorum". Huygens, Leibniz e Johann I Bernoulli si misero al lavoro e nel 1691 apparve un numero memorabile degli "Acta Eruditorum", in cui compaiono gli scritti che contengono le soluzioni proposte dai tre matematici. Huygens giunge alla soluzione del problema utilizzando con perizia il metodo geometrico; Leibniz dà la formula analitica corretta della catenaria in un piano cartesiano di riferimento, anche se nella sua trattazione sono assenti giustificazioni di carattere meccanico; Johann I Bernoulli offre due soluzioni corrette al problema della catenaria e ne enumera ben tredici proprietà. Una ricchezza di soluzioni che, come ha fatto notare Truesdell (1960), mostrano, nell'ordine, la matematica del passato (Huygens), quella del presente (Leibniz) e quella del futuro (Bernoulli).
La ricerca della curva elastica
Un altro importante problema, strettamente legato a quello della fune flessibile e, a parere di Johann I Bernoulli, egualmente interessante, riguarda l'inflessione, o meglio la determinazione della curva elastica caratteristica, di elementi strutturali monodimensionali (travi), sollecitati dal proprio peso o da un sistema di carichi applicati o da qualsivoglia altro genere di azioni (forze) esterne. La palestra dove si esercitano gli studiosi sono ancora gli "Acta Eruditorum" di Lipsia, sui quali nel volgere di pochi anni sono pubblicate numerose e importanti memorie. Jakob I Bernoulli (1694) mette in relazione tra loro il raggio di curvatura ‒ per il quale scrive l'equazione in un sistema cartesiano di riferimento (O,y,z) nella forma:
dove y=y(z) è funzione della variabile z ‒ e una funzione F che dipende dalla sollecitazione esterna (nel caso specifico il momento flettente M); in formula: 1/r=F(M). La sua trattazione tiene conto dell'ipotesi di conservazione delle sezioni piane (le sezioni trasversali della trave si mantengono piane dopo la deformazione) e della legge di Hooke-Bernoulli che, come abbiamo visto, lega lo stato di sollecitazione (le tensioni σ) a quello di deformazione (ε), attraverso un coefficiente di proporzionalità che coincide con il modulo di elasticità del materiale (E). Sebbene la soluzione matematica conseguita da Bernoulli fosse corretta da un punto di vista formale, e pertanto il problema potesse dirsi risolto, la formula ottenuta era poco incoraggiante e le applicazioni difficili e complesse. L'impulso decisivo alla soluzione fu dato da Euler, che formulò una rigorosa giustificazione dell'equazione di Bernoulli e determinò l'equazione della linea deformata di una verga o di una trave elastica nella forma Mx=EJx/r, dove Mx è il momento flettente che agisce nel piano (y,z), Jx è il momento d'inerzia della sezione trasversale della trave, riferito all'asse x baricentrico e ortogonale al piano di riferimento (y,z), E è il modulo di elasticità del materiale e r è il raggio di curvatura; questa equazione stabilisce un legame tra la sollecitazione esterna, prodotta dalle forze e dai pesi agenti sulla struttura, e la curvatura della linea d'asse della trave, inizialmente rettilinea. Nel 1735 Euler risolve l'equazione proposta da Bernoulli calcolando, inoltre, lo spostamento indotto da un carico concentrato applicato sull'estremo libero di una trave a mensola (il 'problema di Galilei'). Allo stesso risultato perviene nel 1741 Daniel Bernoulli, partendo però dall'equazione di Euler prima menzionata e risolvendola nell'ambito della 'teoria linearizzata' della trave elastica. L'anno seguente Daniel Bernoulli propone a Euler di risolvere il seguente problema:
Vostra Signoria potrebbe riflettere un poco se uno non potesse dedurre la curvatura direttamente dai principî della meccanica […]. In ogni caso, per una verga elastica inizialmente rettilinea, io esprimo l'energia potenziale della configurazione inflessa con ∫ds/r2 […]. Poiché nessuno come Voi conosce perfettamente il metodo isoperimetrico, Voi facilmente risolverete questo problema di rendere ∫ds/r2=minimo. (Bernoulli a Euler, 20 ottobre 1742, Fuss 1843)
L'idea di Bernoulli è di ottenere le equazioni dell'equilibrio elastico risolvendo un problema di minimo, imponendo cioè che l'energia potenziale elastica del sistema assuma un valore estremale, compatibile con un sistema di vincoli assegnati sullo stato di spostamento. Euler si mette subito al lavoro e nel 1744 pubblica il già citato scritto Methodus inveniendi lineas curvas, al quale è annesso l'Additamentum I de curvis elasticis dove è ampiamente trattato il tema delle curve elastiche. L'importante contributo di Euler nell'ambito della meccanica ‒ al di là della sua attenzione alla disputa tra i sostenitori di una visione deterministica della realtà fisica fondata sul concetto di 'causa efficiente', e i sostenitori di una visione 'teleonomica' della realtà, fondata invece sul concetto di 'finalità' ‒ si compendia nella risoluzione di questo problema di minimo propostogli da Daniel Bernoulli. La soluzione lo condurrà all'enumerazione delle curve elastiche in numero di nove e alla scoperta del cosiddetto 'carico critico euleriano', ossia di quel particolare valore del carico in corrispondenza del quale un'asta, una trave o una lamina elastica soggetta a un carico assiale s'inflettono in una configurazione variata di equilibrio, distinta da quella iniziale rettilinea ma a essa infinitamente prossima. Il risultato di Euler, relativo al caso della trave incastrata a un solo estremo (o meglio, come aveva suggerito egli stesso, al caso della colonna), ha la forma:
dove i termini indicati hanno il significato già noto e Jmin rappresenta il valore minimo del momento d'inerzia della sezione trasversale della trave. Euler apre così un nuovo capitolo della scienza delle costruzioni, che va oltre il tema della resistenza dei materiali per occuparsi di quello relativo alla stabilità dell'equilibrio; tuttavia, è doveroso sottolineare che i suoi risultati non suscitarono molto interesse tra i matematici e gli ingegneri del tempo.
Euler non abbandonerà tale tema, ritornando successivamente sull'argomento con una memoria dal titolo Sur la force des colonnes, pubblicata nel 1759, in cui discute il problema degli effetti prodotti sull'equilibrio di una colonna da un carico di punta e introducendo una teoria linearizzata per determinare il valore del carico critico in funzione dell'elasticità del materiale e delle dimensioni della colonna. Solamente Lagrange affronterà una trattazione formale delle conseguenze teoriche e astratte che derivano dalla discussione del problema per valori del peso P superiori a quelli del carico critico, in una nota dal titolo Sur la figure des colonnes, pubblicata nel 1770. Nel risolvere il problema di determinare la posizione assunta nella sua configurazione di equilibrio da un filo perfettamente flessibile e elastico, sollecitato nei suoi singoli punti da un sistema di forze, e di ricercare successivamente lo stato di sollecitazione o d'inflessione di ogni suo elemento, Euler darà espressione formale alle 'equazioni indefinite di equilibrio della trave':
Esse esprimono le relazioni intercorrenti fra le caratteristiche di sollecitazione di una trave ‒ individuate dalla forza normale N(z), dalla forza tangenziale T(z) e dal momento flettente M(z), in corrispondenza di una generica sezione trasversale della trave ‒ e i carichi esterni p(z) e q(z), rispettivamente agenti in direzione assiale e trasversale rispetto alla linea d'asse della trave.
La polemica sulle corde vibranti
Nel 1749 d'Alembert aveva pubblicato una memoria il cui argomento aveva suscitato grande interesse tra i meccanici suoi contemporanei; essa riguardava il modo di rappresentare la vibrazione nel piano di una corda fissata ai suoi estremi. Il problema era già stato affrontato da Johann I Bernoulli nel 1727, seppure nel caso particolare di un sistema di n masse equidistanti tra loro e collegate da una fune flessibile, inestensibile e priva di peso. D'Alembert risolse il problema generale attraverso un'equazione differenziale alle derivate parziali, detta anche 'equazione delle onde', ∂2y/∂t2=a2(∂2y/∂x2), per la quale riuscì a ottenere l'integrazione in un caso particolare. L'anno successivo Euler intervenne sul tema con un breve saggio dal titolo Sur la vibration des cordes, formulando alcune precisazioni in merito all'equazione di d'Alembert, soprattutto per quanto riguarda la configurazione iniziale della corda, che deve poter essere arbitraria, ed espose una costruzione geometrica della soluzione. In un secolo ricco di polemiche e querelles sui principî della meccanica non poteva sfuggire all'interesse e alla vena polemica di alcuni scienziati anche il tema della vibrazione delle corde elastiche. Limitandoci in questa sede a sintetizzare le conclusioni del dibattito, ricordiamo che la divergenza tra Euler e d'Alembert risiedeva, com'era prevedibile, nella forma da assegnare all'equazione risolutiva del problema, che doveva comunque consentire di rappresentare le diverse configurazioni assunte dalla corda vibrante. Chi alimentò ulteriormente il fuoco della polemica fu nel 1753 Daniel Bernoulli, che suggerì la possibilità di rappresentare la vibrazione di una corda elastica attraverso una serie trigonometrica; tale equazione compendiava sia la soluzione di Euler sia quella di d'Alembert. La questione andò oltre il problema strettamente meccanico, investendo il concetto stesso di funzione, alla definizione della quale si doveva comunque ricondurre la soluzione del problema. Lagrange interverrà alcuni anni dopo su questo tema, trattando nel 1759 il problema della natura e della propagazione del suono, ma operando per una via diversa da quella percorsa da Euler, d'Alembert e Daniel Bernoulli ed elaborando una tecnica nuova (metodo dei moltiplicatori di Lagrange) per integrare l'equazione differenziale che descrive il moto della corda vibrante.
Ulteriori studi sui principî della meccanica
Intorno alla metà del XVIII sec. tre differenti visioni della realtà materiale si dividevano i consensi, e accentuavano i contrasti, tra gli scienziati e i filosofi: il plenum universale cartesiano, prodotto dal concetto di res extensa, che non ammette il vuoto per la sua intrinseca contraddittorietà e dunque è perpetuamente agitato da un complesso sistema di vortici; le 'azioni a distanza' di Newton, che operano, al contrario, attraverso lo spazio vuoto nel quale risiedono tutti i corpi vincolati dalle 'forze d'attrazione'; infine, il sistema delle 'monadi' di Leibniz, elementi costitutivi della realtà materiale e immateriale e pertanto privi di parti e dunque di estensione, meri punti matematici dotati però di specifica identità che distingue ciascuno da tutti gli altri. Queste diverse visioni del mondo e della realtà materiale animavano, anche nell'ambito strettamente meccanico, un intenso dibattito e proponevano diverse formulazioni dei principî disciplinari; ciò aveva come conseguenza immediata differenti orientamenti di ricerca sui medesimi fenomeni conosciuti.
La 'filosofia sperimentale' coltivata da Newton ‒ come lui stesso scrisse nella Recensio libri del 1712 ‒ aveva il compito di "spiegare le cause dei fenomeni che possono venir confermate dall'esperienza" e dunque "non la si deve riempire di opinioni impossibili a spiegare per mezzo dei fenomeni" (p. 79). Tale impostazione concettuale sollevava però alcune importanti questioni. Le leggi della Natura, che a parere di Newton dovevano essere "eterne e universali", erano soltanto verità contingenti, sottomesse alla sola evidenza della verifica sperimentale, e dunque non più verità necessarie? E come si poteva affrontare il problema del vuoto, che Descartes aveva mostrato essere una contradictio in adiecto e Leibniz aveva negato in ragione di un 'superiore' principio di ragion sufficiente che aveva la sua giustificazione nella volontà di Dio?
Prima di proporre una risposta a tali interrogativi, occorre fare alcune considerazioni sull'enigmatico concetto di 'forza' e sul problema della sua corretta misurazione, che diede ampio spazio alla famosa 'querelle sulle forze vive', apertasi nel 1724 a seguito di un concorso promosso dall'Académie Royale des Sciences di Parigi sul tema della communication du mouvement. A partire da un problema a prima vista semplice come, per esempio, quello dell'urto elastico, l'oggetto del contendere risiedeva, come è noto, nel decidere se la forza dovesse essere misurata in base al tempo durante il quale essa agisce (tesi sostenuta dalla scuola cartesiana, che assegnava il primato al concetto di 'quantità di moto'), oppure se la misura della forza dovesse dipendere dallo spazio lungo il quale essa (vis viva) sposta il proprio punto di applicazione (tesi sostenuta dalla scuola di Leibniz, che assegnava il primato all'equazione di bilancio tra 'forze morte e vive'). La questione era indubbiamente accattivante: essa coinvolgeva aspetti controversi, come quello sulla natura del movimento, e d'altro canto indubbiamente enigmatici, come quello dell'impenetrabilità tra i corpi. La questione ‒ come scrisse Newton nella sua già citata Recensio libri ‒ era certamente degna di essere esaminata seriamente e accuratamente. Le idee di Newton avevano trionfato in Inghilterra, mentre nel Continente dominava la cosmologia cartesiana dell'ideale di una scienza puramente meccanica, che influenzava perfino un anticartesiano quale si professava Leibniz. Le dispute passavano facilmente dal piano filosofico a quello metafisico, interessando problemi come la definizione della forma della Terra e coinvolgendo, oltre ai matematici, astronomi, geografi e anche filosofi, come per esempio Maupertuis, alcuni schierati sul versante cartesiano della querelle, altri su quello newtoniano. Si passava dunque da disquisizioni raffinate su problemi squisitamente meccanici, come la gravitazione universale, a pubblicazioni divulgative sull'opera di Newton, come quelle di Voltaire del 1734 e del 1738 e di Algarotti del 1737, utilizzate per meglio diffondere le idee di una scuola o dell'altra.
La tesi della necessità di un experimentum crucis, peraltro sostenuta da Maupertuis, doveva essere la chiave che avrebbe vincolato la nuova scienza a una visione cartesiana oppure a una visione newtoniana del mondo, stabilendo così la validità dell'una piuttosto che dell'altra teoria. Non è questa la sede per approfondire il tema oggetto della controversia, quanto per sottolineare che le verifiche sperimentali promosse dall'Académie confermarono ‒ come abbiamo già avuto modo di ricordare ‒ la teoria newtoniana secondo la quale la Terra è appiattita ai poli. Una prima conseguenza di questa vittoria della scuola di pensiero inglese su quella francese fu la pubblicazione, nel 1759, della traduzione in francese dei Principia mathematica di Newton a opera di Gabrielle-émilie marchesa di Châtelet; fu l'affermazione della fisica di Newton sulla metafisica di Leibniz e sulla fisica di Descartes, definita "una fisica matematica senza matematica". L'applicazione della matematica ai problemi e alle questioni poste dalla meccanica, grazie anche all'ausilio dei nuovi strumenti del calcolo differenziale e integrale, aveva aperto la strada a un nuovo universo matematico sino ad allora sconosciuto, dove la fisica e i suoi principî, dedotti sperimentalmente, potevano essere meglio descritti attraverso un insieme di equazioni differenziali.
Nell'ambito di queste diverse scuole di pensiero, nel XVIII sec. Jacopo Riccati (1676-1754) ricercava una legge generale di ordine matematico, fondata, però, sui principî certi della meccanica e che consentisse di caratterizzare l'elasticità dei corpi senza dover immaginare arbitrarie rappresentazioni mentali della loro intima costituzione fisica. Tale legge, che doveva prevedere un "perpetuo e non interrotto passaggio delle forze vive in morte, e di morte in vive" (Saggio intorno il sistema dell'universo, 1761, p. 169), può tradursi, nel linguaggio odierno, nel principio di conservazione dell'energia. In altri termini, ciò significa che un corpo perfettamente elastico gode della proprietà di conservare in sé l'energia ricevuta dall'esterno convertendola in 'forza morta' (energia potenziale) e di restituirla integralmente nella forma di 'forza viva' (energia in atto), qualora sia liberato dai vincoli che lo trattengono. Secondo Riccati, l'elasticità deriva dunque dall'energia potenziale acquisita e trattenuta dal corpo a seguito della sollecitazione esterna.
Su tutt'altro versante filosofico e scientifico, anche se su temi analoghi, si poneva la ricerca di Ruggero Giuseppe Boscovich (1711-1787). Nella sua teoria sono ben presenti il sistema newtoniano e l'insegnamento di Leibniz. Mentre Riccati era stato capace di trovare un punto di equidistanza tra le scuole di Newton e di Leibniz, respingendone la dimensione metafisica degli assunti, ma accettandone i fecondi principî matematici che consentivano il reciproco coordinamento di un gran numero di fenomeni, Boscovich coniugava insieme l'esistenza obiettiva di una legge delle forze attrattive e repulsive ‒ cui resta associata la definizione dell'ente materiale ‒ e l'inestensione degli elementi primi, simili ai 'punti matematici' o alle monadi leibniziane.
Sulla falsariga e in analogia con la contrapposizione tra queste due differenti scuole di pensiero si colloca anche la contrapposizione tra mécanique analytique e mécanique physique, che fu messa bene in luce nel secolo successivo da Siméon-Denis Poisson (1781-1840), uno dei fondatori della teoria molecolare dell'elasticità. La posizione di Poisson era opposta al discorso programmatico di Lagrange pubblicato nell'Avertissement della Méchanique analitique del 1788. In esso Lagrange aveva proposto di "ridurre la teoria della meccanica e l'arte di risolvere i problemi a essa connessi a formule generali, il cui semplice sviluppo fornisce tutte le equazioni necessarie per la risoluzione di ogni problema" (p. VI); il suo obiettivo era dunque riunire e presentare sotto uno stesso punto di vista i diversi principî sino ad allora trovati per facilitare la soluzione delle questioni di meccanica, mostrandone la dipendenza reciproca, e mettere in grado gli studiosi di emettere giudizi sulla correttezza e sulla portata di tali principî. Lagrange conclude che: "non si troveranno affatto delle figure in quest'opera. I metodi che espongo non richiedono né costruzioni né ragionamenti geometrici o meccanici, ma soltanto operazioni algebriche assoggettate a un andamento regolare e uniforme. Coloro che amano l'analisi vedranno con piacere la meccanica divenire una nuova branca e mi saranno grati di averne esteso così il dominio" (ibidem).
Con la sua Méchanique analitique, Lagrange aveva mutato paradigma e obiettivi alle scienze meccaniche e, di fatto, aveva rivoluzionato lo studio della meccanica. Essa ‒ scriveva Lagrange ‒ si divide in statica (e idrostatica) e in dinamica (e idrodinamica). La statica si fonda sul principio della leva di Archimede, su quello della composizione dei movimenti e sul principio dei lavori virtuali (vitesses virtuelles, nella terminologia lagrangiana), da lui considerato una specie di assioma della meccanica anche se, nella seconda edizione del suo trattato (1811), avverte che tale principio "non era di per sé stesso abbastanza evidente da poter essere assunto come principio primitivo". A parere di Lagrange, il principio delle velocità virtuali rappresenta il cardine di tutta la meccanica, lo strumento che "conduce a un metodo analitico semplicissimo per risolvere tutte le questioni di statica" e che, combinato con il principio di d'Alembert, "fornisce inoltre un metodo analogo per i problemi di dinamica". Tale metodo aveva consentito di ricavare i principî della conservazione delle forze vive e del movimento, il principio delle aree e quello di minima azione, "risultati generali delle leggi della dinamica" e non principî primitivi di questa scienza. All'impostazione teoretica di Lagrange Poisson contrapporrà, nel secolo successivo, la seguente posizione metodologica, relativa a una sua visione dei fondamenti generali della meccanica:
sarebbe desiderabile che i geometri riesaminassero sotto questo punto di vista fisico e conforme alla Natura le principali questioni della meccanica. è stato necessario trattarle in maniera del tutto astratta per scoprire le leggi generali dell'equilibrio e del movimento; e in questo tipo di generalità e d'astrazione Lagrange è andato il più lontano che si possa concepire quando ha sostituito i vincoli fisici dei corpi con equazioni tra le coordinate dei loro differenti punti; questo è ciò che costituisce la Meccanica analitica, ma accanto a tale mirabile concezione si potrebbe parimenti porre la Meccanica fisica, il cui principio unico sarebbe da riportare completamente alle azioni molecolari, che trasmettono da un punto all'altro l'azione di forze date e sono l'intermediario del loro equilibrio. In tal modo non sarebbe più necessario avanzare ipotesi speciali quando si volessero applicare le regole generali della meccanica a questioni particolari. (Mémoire sur l'équilibre et le mouvement des corps élastiques, p. 361)
Il sistema di Boscovich fu successivamente ripreso da Saint-Venant, per il quale la tesi sull'assenza di estensione degli atomi appariva l'unica conclusione coerente e ineccepibile sotto il profilo fisico-matematico, nonostante le obiezioni che gli furono mosse sulla natura puramente metafisica dell'assunto. Questa 'nuova visione del mondo', che prenderà campo nel XVIII sec. e forse ancora di più in quello successivo ‒ tanto da suscitare la sopracitata vibrante esternazione di Poisson e la già menzionata diatriba tra mécanique physique, proposta da Poisson, e mécanique analytique, proposta da Lagrange e ripresa più tardi dai sostenitori dell'assiomatica ‒, si configura come un importante e vasto progetto scientifico che va oltre i principî generali della meccanica, per investire anche settori e discipline più specialistiche e particolari, come la balistica e l'idraulica, cui faremo un breve cenno più avanti. Si tratta di una rivisitazione di quella 'filosofia della Natura' che oltrepassa la metafisica ‒ per secoli rimasta all'ombra del pensiero scolastico postmedievale ‒ per diventare una scienza della realtà assoluta; non più, dunque, un'assoluta giustificazione filosofica della realtà, ma l'assiomatizzazione della realtà fisica in termini matematici. Ciò darà il via a una tendenza nuova nello sviluppo matematico del pensiero meccanico, indirizzata al formalismo puro, dove la scienza è concepita come un sistema ipotetico-deduttivo basato esclusivamente su un insieme di definizioni implicite e formali degli enti fondamentali o primitivi scelti ad arbitrio, seppure appartenenti e compatibili con la realtà naturale.
Già Leibniz, introducendo le sue monadi come "unità reali", enti o punti materiali che possiedono sia la 'realtà' della particella sia l'esattezza del punto matematico (e dunque l'immaterialità di questo ente), aveva aperto il campo a questa nuova concezione del mondo. La ricerca di un 'qualcosa' che potesse essere considerato primo, supremo, universale, assoluto, necessario, eterno, infinito, in contrapposizione al fatto e all'oggetto particolare relativo, contingente, derivato, soggetto al divenire e pertanto destinato a finire, dunque finito; o ancora la ricerca di ciò che è, o si può considerare, immateriale, soprasensibile, metaempirico e trascendente, in contrapposizione a ciò che è, o si considera, fisico, naturale, materiale ed empirico, diede luogo a numerose indagini e fu motivo di studio per molti scienziati, nel tentativo di formulare questa nuova visione 'matematica' della realtà della Natura. La messa a punto di un sistema di assiomi in quanto nozioni generali evidenti di per sé e non dimostrabili, che stiano a fondamento della meccanica e che dunque diano una definizione implicita dei concetti e degli enti fondamentali era la sfida lanciata da Lagrange alla 'meccanica pratica', figlia della 'nuova scienza' di origine galileiana.
Il sistema di Boscovich e con esso i principî della mécanique physique saranno avvertiti, nell'Ottocento, come la più compiuta espressione di quella filosofia della Natura cui abbiamo fatto cenno; finalmente tale filosofia poteva animare un vasto progetto scientifico, stimolato dalla grande perizia matematica di personaggi come Cauchy e Saint-Venant. Tale progetto e la successiva verifica sperimentale con l'ingresso della mécanique physique, auspicata da Poisson e anticipata dalla teoria di Boscovich, necessitava della conferma dell'esistenza di forze attrattive e repulsive tra le particelle materiali; inoltre, essa richiedeva di verificare se la pretesa unificazione tra 'microcosmo' e 'macrocosmo', ossia tra azioni molecolari e la gravitazione universale, corrispondesse effettivamente alla natura delle cose o non fosse altro che un'affascinante immagine del pensiero sempre proteso all'unità e alla semplificazione dei suoi costrutti. Infine, era necessario, oltre che opportuno, indagare sull'esistenza o meno di modelli interpretativi più convincenti che, pur rinunciando all'obiettivo di una totale riunificazione formale dei costrutti teorici, fosse tale da consentire di esprimere in forma semplificata la legge che mette in relazione tra loro le forze attrattive e repulsive tra le particelle. Questo sarà il cammino che, dopo la fondazione della teoria matematica dell'elasticità avvenuta nel XIX sec., verrà intrapreso da numerosi meccanici e fisici italiani alle soglie del XX secolo.
L''Architecture hydraulique': dalle ricerche sulle acque correnti ai fondamenti dell'idraulica
Pur vantando origini antichissime, l'idraulica è una disciplina recente, che soltanto negli ultimi tre secoli ha fondato e consolidato le proprie basi scientifiche, sia nei confronti delle scienze 'pure', come la meccanica, sia nei riguardi di quelle applicate all''arte' dell'ingegnere. La scoperta dei principî che stanno a fondamento delle scienze idrauliche fu un'opera faticosa realizzata nel XVII e XVIII secolo.
Dopo la grande stagione dell'idraulica sperimentale, che vide nel periodo rinascimentale, e in Italia soprattutto, un grande sviluppo e splendore grazie ai contributi di Leonardo da Vinci, Gerolamo Cardano, Giovan Battista Benedetti, Bernardino Baldi, si deve arrivare alla scuola di Galilei e dei suoi allievi Torricelli e Benedetto Castelli, che nel 1628 dà alle stampe il suo trattato Della misura dell'acque correnti, per vedere aperta la strada alla pubblicazione dei grandi trattati d'idraulica del XVII e del XVIII sec., fra i quali ricordiamo quello di Carlo Fontana sulla misura delle acque correnti del 1696. Nel 1644 Evangelista Torricelli pubblica a Firenze il De motu aquarum, in cui enuncia la legge che porta il suo nome: la velocità di fuoriuscita di un liquido da un foro posto sul fondo di un serbatoio è proporzionale alla radice quadrata dell'altezza che separa la superficie libera del liquido dal fondo, ossia questa velocità è uguale a quella che raggiunge una goccia d'acqua che cade liberamente da un'altezza uguale a quella della superficie che delimita superiormente il liquido. Questa legge troverà la sua spiegazione in termini rigorosi nel contesto del calcolo differenziale e integrale, a seguito degli importanti studi di Daniel Bernoulli condotti nella prima metà del XVIII secolo.
Nel XVII sec. gli studi d'idraulica escono dall'ambito italiano e si sviluppano in tutta Europa grazie anche all'opera di Simon Stevin (1548-1620) e di Mariotte, considerato quest'ultimo il padre del metodo sperimentale in Francia. Il suo Traité du mouvement des eaux et des autres corps fluides ‒ pubblicato postumo nel 1686 ‒ orienta lo studio dell'idraulica, analizzando le proprietà dei fluidi e dei liquidi, l'equilibrio dei corpi fluidi pesanti e comprimibili, la misurazione delle acque correnti, la traiettoria delle particelle liquide, la distribuzione delle acque e la resistenza dei tubi alla pressione esercitata dall'acqua. Mariotte riprende lo studio del principio di Torricelli, usando ingegnosi strumenti per verificare sperimentalmente gli assunti proposti. Allo stesso tempo, Domenico Guglielmini (1655-1710), contemporaneo di Mariotte e a pieno titolo considerato il fondatore dell'idraulica in Italia, pubblica importanti trattati sulla misurazione delle acque correnti (1690) e sul moto delle acque nei fiumi (1697), in cui riprende le linee speculative di Castelli e Torricelli, e pone le basi dell'idraulica fluviale. Guglielmini fu il primo a osservare l'esistenza di uno stato uniforme di equilibrio tra l'acqua, che tende ad aumentare la sua velocità quando scorre lungo un piano inclinato, e la resistenza opposta dal letto del fiume.
Intorno alla metà del XVII sec. la figura di Blaise Pascal (1623-1662) domina le scienze idrauliche, con particolare riguardo all'idrostatica. Il suo saggio Équilibre des liqueurs, pubblicato postumo nel 1663, estende le analisi di Stevin e formalizza il concetto di pressione idrostatica, secondo cui in un fluido la pressione si trasmette in modo eguale in ogni direzione. L'importanza del contributo di Pascal risiede nel fatto che egli lancia un ponte tra la dinamica dei corpi rigidi e la dinamica dei fluidi.
Newton ‒ i cui fondamentali contributi all'idraulica spaziano dallo studio dei corpi immersi in un fluido, a quello dei getti d'acqua, del moto ondoso, dei coefficienti di viscosità ‒ stabilì che in un fluido viscoso le sollecitazioni tangenziali sono proporzionali alla velocità relativa del fluido nelle zone adiacenti. In particolare, la velocità del fluido contenuto in un cilindro infinitamente lungo e rotante attorno al proprio asse con una velocità angolare costante varia inversamente alla distanza radiale misurata dall'asse, il che confuta la teoria dei vortici di Descartes.
Nel 1725 compare postumo il Traité du mouvement et de la mesure des eaux coulantes et jaillissantes di Pierre Varignon che, tuttavia, è più rivolto agli aspetti meccanici del problema che a quelli relativi al comportamento dei fluidi. Varignon analizza il problema della fuoriuscita di un liquido da un foro ('problema di Torricelli'), ottenendo lo stesso risultato erroneo di Newton sul fattore moltiplicativo della velocità di efflusso del liquido. Alcuni anni dopo, precisamente nel 1743, Johann I Bernoulli pubblica un trattato, dal titolo Nouvelle hydraulique, in cui espone le sue considerazioni sulla teoria di Newton relativa allo studio della forma che assume la vena d'acqua alla fuoriuscita da una bocca a battente (cateratta), sottolineando come l'ipotesi dello scienziato inglese richieda che la pressione sia nulla ‒ e ciò è fisicamente impossibile ‒ quando l'acqua attraversa la zona di contatto tra la cateratta e l'acqua stagnante attorno a essa. È tuttavia necessario ricordare che per tutto il XVII sec. l'idraulica era stata confinata tra le scienze empiriche; soltanto con l'avvento del calcolo differenziale e integrale, nel secolo successivo, si stabiliscono i principî del moto dei fluidi che portano questa disciplina al livello delle altre scienze meccaniche.
L'inizio dell'idrodinamica teorica si può infatti far risalire, senza alcun dubbio, al trattato di Daniel Bernoulli intitolato Hydrodynamica (1738), in cui l'autore espone con chiarezza di metodi e ricchezza di contenuti i problemi relativi all'equilibrio statico dei fluidi, alla velocità degli efflussi, all'oscillazione dei liquidi, alla conservazione o alla perdita di energia, alle macchine idrauliche, al moto dell'aria o di altri fluidi e molti altri argomenti ancora, che compendiano in modo esaustivo i principî teorici e gli sviluppi applicativi dell'idraulica nei suoi aspetti relativi sia all'idrostatica sia all'idrodinamica; per esempio, egli fu il primo a usare il piezometro per valutare la pressione nelle condotte. L'importanza del lavoro di Daniel Bernoulli si compendia nella definizione del legame fondamentale che esiste tra la velocità di un elemento in una massa liquida e il carico relativo, che è uno dei capisaldi dell'idraulica moderna. Significativa della sua impostazione metodologica è la dimostrazione del teorema che porta il suo nome. Dedotto sulla base dei principî energetici di Huygens e Leibniz, esso stabilisce che nel moto permanente di un liquido perfetto la somma dell'altezza piezometrica (somma della quota geometrica e del carico piezometrico, rapporto tra la pressione e il peso specifico del liquido) e di un termine proporzionale al quadrato della velocità della corrente è costante per ogni traiettoria o linea di corrente (teorema di Bernoulli); precisamente, detti ζ la quota del generico punto occupato dalla linea di corrente (traiettoria), p la pressione nel liquido, γ il peso specifico del liquido, V la velocità, g l'accelerazione di gravità, si può scrivere: ζ+(p/γ)+V2/(2g)=cost. Dunque, secondo Bernoulli, in un liquido perfetto in moto stazionario la somma dell'energia di posizione, dell'energia di pressione e di quella cinetica di ogni particella per tutto lo sviluppo della relativa traiettoria si mantiene costante; ciò corrisponde ad affermare nel caso specifico il principio di conservazione dell'energia.
Il lavoro di Daniel Bernoulli apre la strada a importanti sviluppi dell'idraulica. Nel corso di pochi anni appaiono numerosi trattati che conferiscono a questa disciplina dignità di scienza meccanica e non soltanto di arte empirica. Cercheremo quindi di fare un breve compendio degli studi più significativi. Nel 1744 compare il Traité de l'équilibre et du mouvement des fluides di d'Alembert sui problemi dell'idrodinamica e della meccanica dei fluidi, scienza che necessariamente ‒ a parere dello scienziato francese ‒ doveva essere fondata sulle osservazioni sperimentali, al contrario della meccanica dei solidi, che invece poteva essere fondata sulla base di principî metafisici. Il moto e la resistenza dei fluidi erano problemi alquanto complessi, che potevano indurre facilmente in errore i philosophes à notions incomplètes di cui aveva parlato Leibniz, ma anche quelli più propensi ad assegnare un valore filosofico di carattere metafisico ai principî meccanici utilizzati in questo particolare ambito della scienza. La questione ‒ certamente complessa ‒ risaliva al problema della conservazione delle forze vive che Daniel Bernoulli assumeva come principio e d'Alembert, al contrario, deduceva dal suo 'principio'.
Tre anni dopo, nel 1747, in occasione di un concorso promosso dalla Königliche Preussische Akademie der Wissenschaften (Accademia Reale Prussiana delle Scienze) di Berlino che vide vincitore d'Alembert con la memoria Réflexions sur la cause générale des vents, Daniel Bernoulli si fece portavoce di feroci critiche nei confronti del vincitore definendolo "buon matematico" ma "pessimo fisico". In realtà, il premio era stato attribuito con merito in quanto il lavoro di d'Alembert, pur non risolvendo completamente il problema dal punto di vista matematico, introduceva risultati rilevanti per lo studio dell'aerodinamica. Nel 1750 l'Accademia di Berlino bandì un concorso sul tema dell'idrodinamica e della resistenza dei fluidi che, tuttavia, non vide alcun lavoro meritevole del premio. Successivamente, però, apparve una memoria di d'Alembert ‒ pubblicata a Parigi nel 1752 e dal titolo Essai d'une nouvelle théorie de la résistance des fluides ‒ in cui veniva presentato il 'paradosso idrodinamico' (o paradosso di d'Alembert): se un corpo si muove in un fluido perfetto o, più esattamente, se vi è un moto relativo tra il fluido e il corpo, la risultante delle pressioni esercitate dal fluido sul corpo è nulla. Questo risultato, in assoluto contrasto con l'esperienza, dipende dall'ipotesi che il fluido sia privo di adesione e di viscosità e che il corpo attraversi un fluido ideale, omogeneo e privo di peso.
I Principia motus fluidorum, scritti da Euler nel 1755, rappresentano uno dei punti di riferimento per lo studio della meccanica dei fluidi. In questo testo fondamentale per lo studio dell'idrodinamica, Euler esprime la cosiddetta 'equazione di continuità' di un fluido, che traduce in forma matematica il principio fisico della conservazione della massa, attraverso l'uso delle funzioni potenziali per un fluido incomprimibile. Da tale equazione è possibile determinare l'equazione del moto del fluido anche se ‒ come lo stesso autore ha fatto notare ‒ "non ci è ancora permesso conseguire una conoscenza completa del moto dei fluidi non per insufficienza di principî noti sul moto, ma per mancanza di strumenti di analisi matematica" (p. 274). La difficoltà risiedeva, infatti, nell'integrazione delle equazioni differenziali alle derivate parziali che descrivono il moto di un fluido generico, come peraltro farà successivamente notare Lagrange nella sua Méchanique analitique (1788). Infine, è importante ricordare il contributo di Pierre-Simon de Laplace (1749-1827), il quale introdusse il suo operatore (poi detto 'operatore laplaciano'), esplicitato per la prima volta nel Traité de mécanique céleste edito in cinque volumi dal 1798 al 1825, nello studio dei fenomeni legati all'idrodinamica. Importanti sono i suoi studi sulle onde e sulle maree, oltre a quelli sulla capillarità; tali studi furono sviluppati da un punto di vista applicativo da Franz Joseph von Gerstner (1756-1832), che si occupò anche di macchine idrauliche, della progettazione delle dighe, dello studio del flusso delle acque nei canali e del moto ondoso.
In sintesi, l'equazione indefinita di equilibrio di un fluido si scrive kF=gradp, essendo F il vettore forza riferito all'unità di massa, k la densità del fluido, p la sua pressione in P, che, se il fluido è omogeneo, si può mettere in relazione con la densità, p=f(k). Le equazioni del moto in P dedotte dal principio di d'Alembert si scrivono nel seguente modo:
essendo v la velocità di un punto P del fluido sul quale è applicata la forza F e t il tempo; l'ultima equazione, detta 'equazione di continuità', assume anche la forma
Per determinare lo stato cinetico del fluido, cioè la velocità con cui le varie molecole fluide passano per un determinato punto fisso della massa fluida, posto v=f(P,t), con P (coordinate del punto) e t pensate come variabili indipendenti, si può scrivere:
che rappresenta la forma 'assoluta' dell'equazione di Euler; determinata la velocità v in funzione di P e di t, si dovrà ancora integrare l'equazione dP/dt=v (Marcolongo 1905, p. 389).
Il Settecento fu anche il secolo dell'idraulica sperimentale. Fra gli sperimentatori che lasciarono una traccia importante negli sviluppi di questa disciplina ricordiamo Giovanni Poleni (1683-1761), Francesco Maria De Regi (1720-1794) e il padre barnabita Paolo Frisi (1728-1784). Il marchese Poleni ‒ altrettanto conosciuto per il suo intervento in merito al consolidamento della cupola di S. Pietro in Vaticano ‒ si occupò dell'efflusso dell'acqua da un orifizio (1717) e fissò le leggi dello stramazzo. De Regi si occupò approfonditamente della misurazioni delle acque correnti (1764), mentre Frisi svolse numerose ricerche nel settore dell'idraulica fluviale tra il 1770 e il 1777. La 'scuola italiana' di idraulica sperimentale vide scendere in campo numerosi studiosi, tra i quali ricordiamo Ottaviano Cametti (1711-1789) e Niccolò Carletti (1723-1796 ca.). Per concludere, meritano menzione gli studi condotti da Jacopo Riccati "sopra le leggi della resistenza con la quale i mezzi fluidi ritardano il moto dei corpi solidi" (1722) e quelli sulla "forza con la quale i corpi fluidi urtano nei solidi" (1742), le Epistolae duae hydrostaticae del 1692 di Domenico Guglielmini e, ancora, gli studi condotti da Anton-Maria Lorgna sulle acque correnti pubblicati nel 1777, quelli di Antonio Rocchi sulla misurazione della velocità e della forza dei corpi in movimento applicata ai problemi idrostatici, per continuare con Gregorio Fontana e le sue dissertazioni sull'idrodinamica, sul moto dei corpi nei mezzi resistenti, sulla resistenza dei canali, sulla pressione dell'acqua in moto nei vasi e nei tubi, sugli effetti della forza centrifuga nel moto dei fluidi, per giungere ai maturi studi compiuti da Lagrange agli inizi degli anni Ottanta del XVIII sec. e, infine, alla traduzione nel 1785 da parte di Gregorio Fontana del Traité élémentaire d'hydrodynamique (1771) di Charles Bossut, in due volumi.
In ambito francese, dopo gli importanti studi intrapresi da Mariotte e da Samuel Morland (1625-1695), ricordiamo il contributo di Claude-Antoine Couplet (1642-1722) sulla resistenza dei tubi in pressione e quello di Bernard Forest de Bélidor (1697-1761), che pubblicò un importante trattato, l'Architecture hydraulique (in 2 volumi e 4 tomi), nel quale sono ampiamente sviluppati i temi relativi all'ingegneria idraulica, alla costruzione di macchine (ruote idrauliche, mulini idraulici e a vento, pompe, ecc.) e alle opere marittime di chiuse, canali, dighe, porti. Altri autori si cimentarono su questo difficile terreno delle scienze meccaniche, con risultati comunque interessanti: Henri de Pitot (1695-1771) inventò un dispositivo per misurare la velocità dell'acqua corrente, Antoine de Chézy (1718-1798) stabilì una formula per valutare la velocità dell'acqua in un canale soggetto a una corrente uniforme, formula che trova ancor oggi uso nell'idraulica tecnica. Inoltre, ricordiamo John Smeaton (1724-1792), uno dei primi e più grandi ingegneri inglesi, che si occupò approfonditamente d'idraulica sperimentale, e Jean-Charles Borda (1733-1799), che fece numerosi esperimenti sulla resistenza dei fluidi e sull'efflusso dei liquidi dai fori di un recipiente. Charles Bossut, ricordato poco sopra per il suo trattato d'idrodinamica, sviluppò numerose ricerche d'idrodinamica e d'idraulica sperimentale, mentre Pierre-Louis-Georges Du Buat (1734-1809) studiò vari fenomeni legati al moto dei fluidi nelle condotte e nei canali, descrivendo la velocità di efflusso dell'acqua da un orifizio, la resistenza dei tubi in pressione e formulando un metodo semiempirico per valutare la sezione dei canali simile a quello proposto da Chézy. Infine, è doveroso ricordare gli studi di Giovanni Battista Venturi (1746-1822) e di Reinhard Woltman (1757-1837) sulla misurazione della resistenza dei tubi in pressione e sul moto delle acque nelle condotte e nei canali.
Verso la fine del secolo e gli inizi di quello successivo, il grande numero di studi e ricerche favorì la stampa di numerosi saggi e trattati sull'idraulica e sulle sue applicazioni all'ingegneria; tra questi ricordiamo le opere di Pons-Joseph Bernard (1787), Gaspard de Prony (1790, 1802, 1804), Pierre-Simon Girard (1804) e François-Michel Lecreulx (1809), che anticipano quella rivoluzione editoriale che diffonderà in modo cospicuo le nuove scoperte in ambito scientifico. Fra i molti merita una menzione particolare il fondamentale saggio di architettura idraulica pubblicato nel 1790 da Gaspard-François-Clair-Marie Riche de Prony (1755-1839), che ebbe una vasta diffusione nell'ambito delle scienze e delle 'arti' dell'ingegnere, in quanto dedicato a tutti coloro che erano interessati, oltre ai principî fondamentali della disciplina, anche alla costruzione di macchine di ogni genere e tipo per sollevare e canalizzare le acque, e a molto altro ancora.
'L'art de jetter les bombes': la scienza balistica
La 'balistica esterna' è uno dei temi che più ha affascinato gli studiosi del Settecento, perché legata alla scienza del moto e soprattutto al problema del movimento di un corpo lanciato ('proietto') attraverso un mezzo resistente (si chiama invece 'balistica interna' la disciplina dei fenomeni chimico-fisici che avvengono nella canna dell'arma nell'atto del lancio del proietto). Le sue origini risalgono alla metà del XVI sec., contestualmente all'uso delle armi da fuoco nell'arte della guerra. Dei problemi della balistica esterna si sono occupati i maggiori matematici e fisici, a partire da Niccolò Tartaglia per arrivare a Galilei, Newton, e molti altri ancora, durante un lungo periodo di ricerca durato più di quattro secoli.
Nel 1537 Tartaglia afferma, per primo, che la traiettoria percorsa da un proietto nell'aria non può essere perfettamente rettilinea in alcuna sua parte, che l'angolo di massima gittata non può superare 45° e che, inoltre, con angoli complementari si ottengono gittate uguali. Un secolo dopo, Galilei, facendo astrazione della resistenza dell'aria, concepisce il moto del proietto come risultante di due movimenti, uno rettilineo e uniforme, l'altro verticale e con intensità variabile secondo una legge uniforme, e ne deduce che in queste particolari condizioni la traiettoria è una parabola. Successivamente, la teoria del moto dei proietti dello scienziato pisano fu rivisitata nel 1644 da Torricelli, perfezionata nel 1739 da Guido Grandi (1671-1742) e integrata nel 1783 dagli studi di Paolo Frisi.
Verso la fine del XVII sec. compaiono due testi, fondamentali per lo studio della scienza balistica sia dal punto di vista meccanico sia da quello più propriamente sperimentale o dell''artigliere pratico'. Nel 1674 Robert Anderson (1668-1696) pubblica a Londra The genuine use and effects of the gunne, trattato che diventerà in breve un importante punto di riferimento per tutti coloro che si occupano di balistica esterna. Alcuni anni dopo, ossia nel 1683, Nicolas-François Blondel (1618-1686) pubblica a Parigi il suo trattato su L'art de jetter les bombes. Questi due testi si pongono a fondamento di un'arte e di una scienza balistica che, forti degli studi condotti da Galilei, Torricelli e Marin Mersenne, introdurranno sensibili modifiche nella pratica d'artiglieria insegnata nelle scuole militari. In ambedue gli studi, tuttavia, il problema meccanico non è ancora completamente chiarito; infatti, gli autori non tengono sufficientemente conto dell'effetto della resistenza dell'aria sul moto dei proietti, problema peraltro già sollevato da James Gregory (1638-1675) nel 1672. L'ipotesi di Gregory era la seguente: per tenere conto della resistenza dell'aria, è necessario assumere che il moto del proietto debba essere composto di un movimento verticale uniformemente accelerato e di un movimento uniformemente ritardato secondo la linea di proiezione. L'ipotesi di Gregory diede luogo a una querelle che vide coinvolti, oltre allo stesso Gregory, Robert Anderson, John Collins, John Wallis e Newton. In sintesi, Collins era dell'avviso che la parabola proposta da Anderson fosse senza alcun valore di carattere pratico per gli artiglieri, mentre la soluzione di Gregory non gli sembrava ben fondata dal punto di vista matematico. Newton, nel 1674, sottolineò che il libro di Anderson, sicuramente molto ingegnoso nella formulazione dei principî esposti, sarebbe stato di grande utilità se tutti questi fossero stati dimostrati veri, mettendo dunque in dubbio l'ipotesi del moto parabolico nel caso in cui si fosse tenuto conto della resistenza dell'aria. Wallis, nel 1687, evidenziò invece la necessità di prendere in esame il caso in cui la resistenza del mezzo è proporzionale alla velocità. Ancora Newton (nel 1684 con il De motu e successivamente, nel 1687, nei Principia) ritornò sull'argomento del moto dei proietti attraverso un mezzo resistente, analizzando i due casi in cui, rispettivamente, la resistenza è supposta proporzionale alla velocità del proietto in un moto rettilineo uniforme, oppure è ipotizzata proporzionale al quadrato della velocità nel caso di moto ascendente e discendente. Occorre sottolineare che lo stesso Newton affermò successivamente che l'ipotesi secondo la quale la resistenza opposta dal mezzo è proporzionale alla velocità del corpo che lo attraversa è più matematica che conforme alla natura dei fatti, riportando agli onori della scienza gli studi condotti nel 1690 da Robert Hooke e quelli svolti per conto dell'Académie Royale des Sciences di Parigi negli anni 1668-1669. Il lavoro di Newton si può riassumere nel seguente modo. Il problema del moto in un mezzo resistente mette in campo una relazione che caratterizza la variazione della velocità e si sviluppa attraverso il seguente percorso: il riconoscimento di alcune correlazioni tra gli enti in gioco, suscettibili di una trattazione per via geometrica; l'ipotesi di assimilare il moto di un corpo a una successione di piccoli movimenti uniformi. In questa prospettiva, la conclusione di Newton è che la soluzione di ciascun problema può essere conseguita passo dopo passo finché ‒ come osserverà Varignon ‒ sarà possibile una traduzione del problema in termini geometrici. Si deve quindi a Newton se il problema è stato affrontato con perizia e rigore, e risolto analiticamente nel caso in cui la resistenza del mezzo è proporzionale alla velocità. Tuttavia, soltanto l'introduzione del calcolo differenziale e integrale ‒ e a fortiori una concettualizzazione differenziale della scienza del moto ‒ permetteranno di pervenire alle equazioni generali del movimento e di risolvere, finalmente attraverso procedimenti e algoritmi di differenziazione e integrazione ben definiti, i problemi del moto di un corpo in un mezzo resistente.
La strada era dunque tracciata e si trattava soltanto di percorrerla. Nel 1689 Leibniz pubblica negli "Acta Eruditorum" un breve saggio sul moto dei proietti, che conferma in sostanza i risultati di Newton pubblicati nei Principia del 1687 e in parte quelli di Huygens del 1690. Le soluzioni esposte da Leibniz, relative al problema del moto dei proietti attraverso un mezzo resistente, si fondano tutte sul seguente 'principio generale': gli spazi percorsi (dp) sono in ragione composta delle velocità (v) e dei tempi (dt) o meglio "dp ut vdt", come egli ebbe motivo di scrivere. Circa dieci anni dopo, precisamente nel 1698, Varignon introduce il concetto di 'velocità istantanea', peraltro già intuito da Newton e Leibniz, e successivamente quello di 'forza acceleratrice istantanea'. Varignon, come già avevano fatto Galilei e Newton, elabora la sua scienza del moto sulla base di una definizione non esplicita ma operante di velocità istantanea. L'importanza della sua impostazione metodologica consiste nell'elaborazione di un algoritmo che consente di ridurre le questioni relative al moto a puri problemi di calcolo.
All'inizio del secolo successivo, negli anni che intercorrono tra il 1707 e il 1711, Varignon pubblica nei "Mémoires de l'Académie Royale des Sciences" di Parigi ben dodici memorie relative al moto di un proietto attraverso un mezzo resistente. Sulla base del nuovo calcolo leibniziano, lo scienziato francese riorganizza e generalizza i risultati precedentemente ottenuti da Newton, Huygens, Leibniz e Wallis. Egli introduce le importanti definizioni di 'resistenza istantanea' (la resistenza che un mezzo oppone, in ciascun istante, a un corpo che lo attraversa, e che deve essere proporzionale alla diminuzione di velocità subita dal corpo medesimo nello stesso intervallo di tempo) e di 'velocità istantanea'; stabilisce la legge generale che caratterizza il moto secondo traiettorie rettilinee attraverso un mezzo resistente, nella forma
dove F(u) rappresenta la forza esercitata dal mezzo in funzione della velocità u, f(t) è l'accelerazione all'istante iniziale e k un coefficiente balistico. In questo modo Varignon è in grado di risolvere numerosi problemi, in particolare determinando quando la resistenza del mezzo è proporzionale alla velocità, o al quadrato della velocità, o addirittura a una potenza qualunque della velocità, e, ancora, relativamente alla somma della velocità con il suo quadrato, al moto verticale, alla traiettoria descritta da un mobile dotato di peso proprio lanciato obliquamente in un mezzo dove la resistenza è proporzionale alla velocità (balistica curvilinea).
Occorre comunque aspettare soltanto alcuni anni per vedere risolto il problema dell'integrazione delle equazioni del moto di un proietto. Nel 1719 Johann I Bernoulli riesce a integrare le equazioni del moto del proietto nel caso di resistenza proporzionale a una potenza qualsiasi della velocità e risolve il problema ‒ posto da Newton nei Principia (Libro II, prop. 10) ‒ di trovare la curva che un proietto descrive nell'aria, nell'ipotesi che la gravità e la densità siano costanti, e nel caso in cui la resistenza offerta dall'aria sia in ragione del quadrato della velocità. Nikolaus I Bernoulli (1687-1759), nipote di Johann I, aveva già risolto un problema simile, nel caso in cui la dipendenza tra resistenza dell'aria e velocità si può tradurre nella relazione f(v)=a+bvn, con a, b, n costanti; nel caso particolare in cui si ponga a=0, la soluzione di Nikolaus I Bernoulli corrispondente a n=2 riguarda le resistenze idrauliche. L'analisi di Johann I Bernoulli è significativa e ricca di prospettive future, a motivo dell'uso molto abile della composizione delle accelerazioni secondo le direzioni tangente e normale alla traiettoria. Alle ricerche di Johann I Bernoulli e Newton si ricollegano negli anni seguenti quelle portate avanti da Euler, d'Alembert e, successivamente, dal generale prussiano Jacob Christian Friedrich Otto. In particolare, Johann I Bernoulli e d'Alembert determinano la soluzione dell'equazione del moto di un punto materiale attraverso un mezzo resistente, in alcuni casi ben specifici.
Nel contesto delle scienze legate all'artiglieria, e dunque agli usi militari della balistica, il Settecento è stato un secolo che ha visto la pubblicazione di numerosi manuali il cui scopo era, oltre che fondare e sviluppare una disciplina peraltro estremamente importante per l'arte della guerra, anche fornire agli ufficiali del settore strumenti di informazione atti a migliorare l'uso dell'artiglieria nelle battaglie, che in quel secolo si susseguirono con una certa frequenza. Questi studi daranno il via a una consistente pubblicistica 'tecnica', che vedrà alle stampe numerosi volumi esplicativi dell'uso di tavole balistiche per il tiro d'artiglieria. In ambito italiano ricordiamo le opere di Andrea Musalo (1702), Giovanni Maria Gilmotti (1713) e Gaetano Marzagaglia (1748). Molta attenzione fu dedicata all'istruzione dei giovani ufficiali dell'esercito nell'uso delle armi da fuoco e dell'artiglieria in generale, con particolare attenzione anche ai principî della balistica. Tra i maggiori divulgatori di questa disciplina spicca Alessandro Vittorio D'Antoni Papacino (1714-1786), direttore della Scuola d'artiglieria di Torino, le cui opere ebbero diffusione anche nei paesi di lingua inglese e francese. Nel 1731 compare il trattato di Bernard Forest de Bélidor dal curioso titolo Le bombardier françois, ou nouvelle méthode de jetter les bombes avec précision, manuale a uso degli artiglieri con alcuni cenni di balistica, superato soltanto verso la fine del secolo dall'importante manuale compilato nel 1787 da Jean-Louis Lombard (1723-1794), quest'ultimo sicuramente dedicato agli ufficiali che si occupano del tiro d'artiglieria e, pertanto, arricchito da numerose tabelle di uso pratico. Lo stesso Lombard pubblicherà dieci anni dopo un interessante volume sul moto dei proietti che vedrà ampia diffusione nelle scuole di artiglieria.
Nel 1741, una scoperta importante, l'invenzione del 'pendolo balistico', consente di determinare sperimentalmente la velocità iniziale di un proietto lanciato da una bocca da fuoco. Alcuni anni dopo, esattamente nel 1767, Gregorio Casali (1721-1802) pubblica un articolo in cui afferma di avere inventato una macchina in grado di dimostrare sperimentalmente i teoremi di Galilei e di 'sGravesande sulla teoria del moto dei proietti, ma soltanto nel 1771 Anton-Maria Lorgna redige una 'tavoletta balistica' che avrà una grande fortuna, soprattutto in Germania grazie anche alla sua pubblicazione nel "Magazin für Ingenieur".
Verso la fine del secolo, precisamente nel 1782, scende in campo anche Adrien-Marie Legendre (1752-1833), concorrendo a un premio messo in palio dall'Accademia delle Scienze di Berlino con una memoria in cui tratta della traiettoria dei proietti attraverso i mezzi resistenti. In questo importante lavoro Legendre definisce l'equazione corretta della traiettoria di un proietto. L'anno seguente compare a Digione la traduzione del testo di Benjamin Robins (1707-1751) sui principî di artiglieria, tradotto dal tedesco con note e commenti di Euler, un testo fondamentale che avrà un grande successo nelle scuole di artiglieria europee. Successivamente, nel 1789, Lagrange pubblica nel "Journal de l'École Polytechnique" le formule relative al moto dei proietti all'interno delle canne dei cannoni e apre, di fatto, gli studi sulla balistica interna, al cui sviluppo contribuirà in misura maggiore la pratica sperimentale, sviluppando sia il tema della 'pirostatica', che studia la combustione della polvere da sparo a volume costante, sia quello della 'pirodinamica', che studia invece la combustione della polvere da sparo a volume variabile entro la bocca da fuoco.
Saranno infine gli studi intrapresi a partire dal 1782 da Charles Hutton (1737-1823) ad anticipare i temi che verranno sviluppati dalla scienza balistica nel XIX secolo. Hutton affronta il problema della forza impressa ai proietti, della gittata dei cannoni in funzione dell'elevazione del tiro, della resistenza che l'aria oppone al moto dei proietti, degli effetti prodotti dalla lunghezza della canna del cannone sul tiro d'artiglieria e dell'influenza che esercita la carica delle polveri nell'imporre un'adeguata accelerazione al proietto e aumentarne così potenza e gittata. Si dovrà tuttavia aspettare la metà del XIX sec., quando nel 1855 Paolo Ballada di Saint-Robert (1815-1888) ‒ ufficiale piemontese che ideò i proietti lenticolari e i cannoni ad anima curva ‒ pubblicherà un interessante trattato dal titolo Del moto di proietti nei mezzi resistenti, per giungere a una forma semplice delle equazioni differenziali del moto e pervenire a un'esplicita formulazione delle proprietà della traiettoria dei proietti; infine, nel XX sec., grazie agli studi di Mauro Picone (1885-1977), Antonio Signorini (1888-1963) e soprattutto Angelo Francesco Siacci (1839-1907), si giungerà a una soluzione semplice e pratica dei problemi connessi alla 'balistica esterna', ricondotti all'adozione di una tavola di tiro di facile uso che prende il nome di 'tavola balistica generale'.
© Istituto della Enciclopedia Italiana - Riproduzione riservata