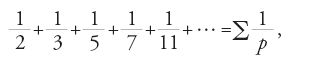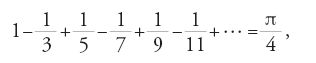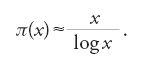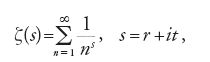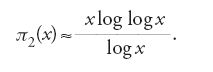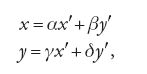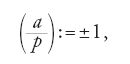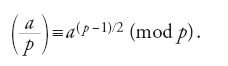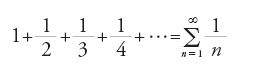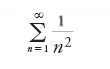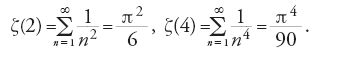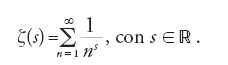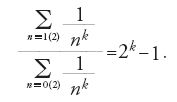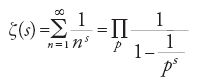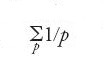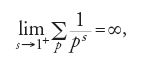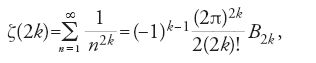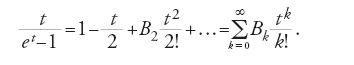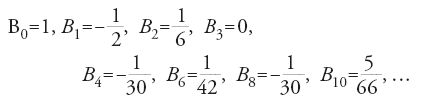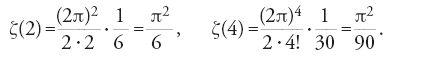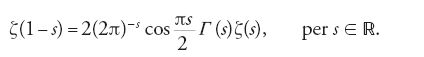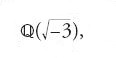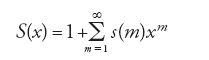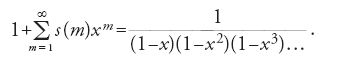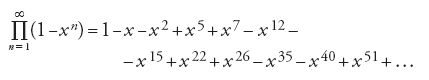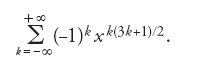L'Età dei Lumi: matematica. La teoria dei numeri

L'Eta dei Lumi: matematica. La teoria dei numeri

La teoria dei numeri

La teoria dei numeri (o aritmetica) tratta delle proprietà dei numeri. Lungo tutta la sua storia, un tema dominante è stato lo studio delle soluzioni delle cosiddette 'equazioni diofantee'. Si tratta di equazioni polinomiali con coefficienti interi (o razionali), del tipo f(x,y,z,...)=m, in cui m è un numero intero, delle quali si cercano soluzioni intere (o razionali) x,y,z,.... Il loro nome deriva da Diofanto di Alessandria (250 d.C. ca.), che nell'opera Arithmetica trattò diverse equazioni di questo tipo, di primo, secondo, terzo e perfino quarto grado, con due, tre o anche più incognite.

La moderna teoria dei numeri ha inizio con l'edizione dell'Arithmetica di Diofanto a cura di Claude-Gaspard Bachet de Méziriac, nel 1621. Pierre de Fermat (1601-1665), fondatore della moderna teoria dei numeri, studiò attentamente questa edizione intorno al 1638 scoprendo molti nuovi teoremi aritmetici, per la maggior parte legati a problemi diofantei di secondo e terzo grado. A questo scopo si servì non soltanto delle proprietà di divisibilità, ma anche di quelle, più sottili, dei resti della divisione per un intero (positivo) fissato. Fermat non diede quasi mai dimostrazioni dei suoi teoremi, che furono fornite invece per lo più dal matematico svizzero Leonhard Euler (1707-1783), il quale arricchì la teoria dei numeri di molte scoperte originali. Euler fu in effetti la figura di maggior spicco del XVIII sec., non soltanto per quanto riguarda la teoria dei numeri ma per la matematica nel suo complesso. Altri importanti studiosi della teoria dei numeri dell'epoca furono Joseph-Louis Lagrange (1736-1813) e Adrien-Marie Legendre (1752-1833), due matematici che portarono avanti le ricerche di Euler nella seconda metà del XVIII sec., in parte con l'aiuto dello stesso Euler.

I principali oggetti di studio nel Settecento erano la teoria elementare dei numeri, i problemi diofantei del secondo ordine e i problemi inerenti i campi algebrici quadratici, in particolare le forme quadratiche e l'equazione di Pell, le frazioni continue e le teorie dei numeri additiva e analitica.

La maggior parte delle scoperte riguardanti la teoria dei numeri è contenuta nell'opera di Legendre Essai sur la théorie des nombres (1798), la prima dedicata interamente all'aritmetica. Lo status della teoria dei numeri all'epoca era ancora quello di una scienza empirica che non poteva competere con le teorie geometriche già ben consolidate o con il calcolo differenziale e integrale, e non attraeva quindi molta attenzione, nonostante matematici eminenti come Fermat, Euler, Lagrange, Legendre dedicassero una parte rilevante del loro tempo a problemi aritmetici. Questo stato di cose cambiò soltanto in seguito alla pubblicazione del trattato fondamentale di Carl Friedrich Gauss Disquisitiones arithmeticae (1801), in cui la teoria dei numeri è organizzata in modo assiomatico nello stile che Euclide aveva adottato per la geometria.

Teoria elementare dei numeri

Numeri perfetti

La teoria dei 'numeri perfetti' e dei 'numeri amicabili' risale alla scuola pitagorica nel VI sec. a.C. L'aritmetica pitagorica è esposta nei tredici volumi degli Elementi di Euclide, i cui Libri VII, VIII e IX trattano della teoria dei numeri. Nel Libro IX (prop. 36) Euclide dimostra il seguente teorema (teorema 1.1): se la somma 1+2+2²+...+2ⁿ⁻¹=2ⁿ−1=p è un numero primo, allora 2ⁿ⁻¹p=m è un numero perfetto; m è definito numero perfetto se la somma dei suoi divisori propri (cioè diversi dall'unità e dal numero stesso) è uguale a m.

La dimostrazione del teorema 1.1 si può fondare interamente sulla teoria dei numeri pari e dispari (cioè delle congruenze modulo 4) sviluppata dalla scuola pitagorica. Nicomaco di Gerasa (100 d.C. ca.), nella sua Introduzione all'aritmetica, fornì i primi quattro esempi di numeri perfetti, e cioè 6, 28, 496 e 8128, corrispondenti agli esponenti n=2, 3, 5, 7. Pietro Antonio Cataldi (1552-1626) nel 1607 e Fermat in una lettera a Mersenne del giugno 1610 affermarono che, affinché p=2ⁿ−1 sia un numero primo, è necessario che lo sia n, e Cataldi verificò che 2ⁿ−1 è un numero primo per n=13, 17 e 19, ottenendo in tal modo i successivi tre numeri perfetti. Non è noto se vi sia un numero infinito di numeri perfetti. In un lavoro sui numeri amicabili, pubblicato postumo nel 1849, Euler dimostrò l'inverso del teorema 1.1, e cioè (teorema 1.2): se m è un numero perfetto pari, m è necessariamente della forma m=2ⁿ⁻¹p, dove p=2ⁿ‒1 è un numero primo.

Il problema dell'esistenza di numeri perfetti dispari rimane ancora aperto.

Numeri amicabili

Per quanto riguarda i numeri amicabili, Pitagora ne fornì un primo esempio, ossia la coppia 220 e 284. Due numeri a e b si dicono 'amicabili' se ciascuno è la somma dei divisori propri dell'altro. Un'altra coppia di numeri amicabili fu trovata da Fermat nel 1636 e Descartes, in una lettera a Mersenne nel 1638, fornì una terza coppia. In due lavori sui numeri amicabili, De numeris amicabilibus, Euler ne trovò complessivamente 59 nuove coppie. Il primo di tali lavori, del 1747, è un articolo di due pagine, mentre l'altro è più lungo, pubblicato nel 1750 ma completato anch'esso già nel 1747. La lista compilata da Euler nel 1747 conteneva 30 coppie, mentre la lista del 1750 comprendeva, oltre a due coppie speciali, 62 coppie, incluse le tre già note e due che dovette correggere. Da allora sono state trovate molte altre coppie, ma non si sa ancora se vi sia un numero infinito di coppie di numeri amicabili.

Numeri di Mersenne

Data la connessione con i numeri perfetti, e considerando il teorema secondo il quale, affinché p=2ⁿ−1 sia primo, n dev'essere primo, la ricerca dei numeri primi della forma p=2ⁿ−1, chiamati oggi numeri primi di Mersenne, è stata da allora uno degli argomenti più studiati. Nel 1738 Euler dimostrò che molti numeri della forma p=2ⁿ−1 non sono primi anche se n è primo. Egli aveva elaborato a questo scopo alcuni criteri di divisibilità per i numeri di Mersenne e aveva scoperto anche il numero primo successivo a quelli già noti (comunicandolo in una lettera a Johann III Bernoulli nel 1771), dimostrando che p=2ⁿ−1 è un numero primo per n=31. Questo numero primo di Mersenne rimase il più grande numero primo noto per tutto il XVIII secolo. Soltanto verso la fine del XIX sec. furono scoperti numeri primi di Mersenne più grandi.

Numeri di Fermat

I numeri primi della forma p=2²ⁿ+1 sono chiamati numeri primi di Fermat. In diverse lettere ai suoi corrispondenti, a partire dal 1640, Fermat affermò che tutti i numeri della forma 2²ⁿ+1 sono primi, per qualunque numero naturale n. L'affermazione risulta in effetti vera per n=0, 1, 2, 3, 4. Euler nel 1732 riuscì però a dimostrare che 2²ⁿ+1 non è un numero primo per n=5, poiché contiene il fattore 641. In effetti, tutti i numeri della forma 2²ⁿ+1 con n>4 studiati finora si sono rivelati non primi. I numeri primi di Fermat giocano un ruolo importante nella teoria di Gauss della ciclotomia (1801), cioè della costruzione dei poligoni regolari con riga e compasso.

Congruenze

Il 'piccolo' teorema di Fermat

In relazione allo studio dei numeri primi della forma p=2ⁿ−1, Fermat scoprì nel 1640 (come risulta da una lettera a Bernard Frénicle de Bessy) una proprietà fondamentale per la teoria delle equazioni diofantee di grado superiore, e cioè il 'piccolo' teorema di Fermat (teorema 2.1): per qualsiasi numero primo p e qualsiasi intero a, a^p e a danno lo stesso resto se divisi per p, ovvero a^p−a è divisibile per p. In simboli:

[1] a^p≡a (mod p).

In altre parole: per qualsiasi primo p e qualsiasi intero a non divisibile per p, a^p−1 dà 1 come resto della divisione per p; in simboli:

[2] a^p-1≡1 (mod p).

Il teorema fu dimostrato da Euler nel 1736 (e prima di lui da Leibniz in un manoscritto del 1680 ca.). Studiando i numeri primi p della forma x²+Ny²=pz, per x, y, z interi e un intero dato N, Euler scoprì nel 1760 un'importante generalizzazione del teorema di Fermat, e cioè una generalizzazione dai numeri primi p a qualsiasi intero positivo m. Questo cosiddetto 'teorema di Euler' afferma che (teorema 2.2): per qualsiasi intero a primo con m si ha:

[3] a^φ(m)≡1 (mod m),

in cui φ(m) è la cosiddetta 'funzione di Euler', che conta il numero di interi tra 0 e m che sono primi con m.

Campi finiti

Quest'ultimo risultato fu ottenuto da Euler nel 1760 attraverso uno studio accurato della struttura dei resti rispetto a un dato intero m. Euler ne dedusse il seguente teorema, che risulta fondamentale per le congruenze modulo un numero primo, e cioè (teorema 2.3): i resti rispetto a un numero primo p formano un 'campo'.

Ciò significa che si possono effettuare sui resti (o più precisamente sulle classi dei resti) tutte le quattro operazioni elementari senza restrizioni, eccetto la divisione per zero. I resti hanno dunque le stesse proprietà algebriche dei numeri razionali. Inoltre, i p−1 resti non nulli formano un gruppo ciclico rispetto alla moltiplicazione, generato da una delle cosiddette 'radici primitive modulo p'; ricordiamo che a è radice primitiva del numero primo p se p−1 è il minimo esponente positivo x per cui a^x≡1 (mod p).

Da quest'ultima scoperta Euler fu in grado di ricavare facilmente, nel 1773, il teorema di Wilson, anche se la sua dimostrazione (dell'esistenza di una radice primitiva modulo p) non era del tutto completa. Il teorema fu attribuito da Edward Waring (1770) a Sir John Wilson (1741-1793), ma era già noto a Leibniz prima del 1683. Il teorema afferma che (teorema 2.4): qualsiasi numero primo m gode della proprietà

[4] 1∙2∙3…(m-1)≡-1 (mod m).

Il primo a dimostrare il teorema di Wilson fu comunque Lagrange nel 1771, che lo dedusse dal teorema di Fermat. Lagrange dimostrò inoltre l'inverso del teorema di Wilson, anch'esso già noto a Leibniz, cioè (teorema 2.5): se m è un numero naturale che gode della proprietà

[5] 1∙2∙3…(m-1)≡-1 (mod m).

allora m è un numero primo.

Congruenze per i polinomi

Un altro teorema fondamentale per la teoria delle congruenze, dimostrato da Lagrange nel 1768, è il seguente (teorema 2.6): se p è un numero primo e f(x) è un polinomio di grado n a coefficienti interi, il cui coefficiente del termine di grado massimo non è divisibile per p, vi sono al più n interi x tra −p/2 e p/2 tali che f(x) è divisibile per p; secondo la moderna terminologia: la congruenza f(x)≡0 (mod p) ha al più n soluzioni distinte modulo p.

Questo teorema rappresenta per le congruenze l'analogo di un teorema che deriva dagli studi compiuti da Descartes nel suo libro La géométrie (1637), secondo il quale un polinomio di grado n a coefficienti interi o razionali possiede al più n radici distinte.

Il criterio di Euler

Proseguendo i suoi studi sulle estensioni del teorema di Fermat, Euler scoprì un criterio fondamentale per le equazioni diofantee di secondo grado o di grado superiore. Tale criterio, conosciuto oggi come 'criterio di Euler dei residui di potenza' afferma che (teorema 2.7): se p è un numero primo della forma p=tn+1, con t e n numeri naturali, e a è un qualsiasi intero non divisibile per p, allora l'equazione a−xⁿ=py ha soluzioni per x e y interi se e solo se a^t−1=pz è risolubile per z intero.

In altre parole: se p è un numero primo della forma p=tn+1, a è un intero non divisibile per p, e n e t sono interi positivi, a≡xⁿ (mod p) è risolubile per x intero se e solo se a^t≡1 (mod p).

Questo risultato deriva dal teorema 2.3, e fu formulato e dimostrato da Euler nel suo articolo Theoremata circa divisores numerorum del 1747 (theoremata 11, 13 e 14), e ancora nel Theorema circa residua ex divisione potestatum relicta del 1758 (theorema 18).

Numeri primi

Numeri primi nelle progressioni aritmetiche

Già Euclide, nei suoi Elementi aveva dimostrato che vi è un numero infinito di numeri primi. Euler, nel 1737, ricavò con metodi analitici un risultato molto più forte, e cioè il fatto che i numeri primi superano in numero i quadrati. Fu possibile ricavare questo risultato dimostrando che la serie

ottenuta sommando su tutti i numeri primi p, è infinita. Con lo stesso metodo analitico, partendo dalla serie di Leibniz:

Euler dimostrò nei suoi Opuscula analytica 2 che le due progressioni aritmetiche 4x+1 e 4x−1 contengono entrambe infiniti numeri primi (De summa seriei ex numeris primis formatae, 1775; pubblicato nel 1785). Nell'articolo 2 della stessa opera Euler affermava anche che qualunque progressione aritmetica del tipo mx+r, con m e r numeri naturali primi tra loro, contiene infiniti numeri primi. La validità di questo risultato era stata ipotizzata anche da Legendre, al quale serviva per dimostrare la legge della reciprocità dei residui quadratici. Il teorema generale sulle progressioni aritmetiche fu però dimostrato soltanto da Peter Gustav Lejeune Dirichlet nel 1837, che per questo dovette estendere e approfondire considerevolmente il metodo di Euler.

Polinomi generatori di numeri primi

Oltre allo studio della rappresentazione di numeri primi mediante polinomi di primo grado, fu affrontato anche il problema, molto più difficile, della rappresentazione dei numeri primi per mezzo di polinomi di grado superiore. Euler notò nel 1772 che il polinomio x²−x+41 rappresenta numeri primi soltanto per x=1, ..., 40, mentre nel 1762 aveva già rilevato che lo stesso vale per x²+x+17, se x=0, 1, ..., 16 (dovendo poi però escludere il 16). Legendre citò il fatto che 2x²+29 rappresenta numeri primi solamente per x=0, 1, ..., 28 e x²+x+41 rappresenta numeri primi soltanto per x=0, 1, …, 39. Quest'ultimo risultato si ricava dal polinomio di Euler x²−x+41 mediante la trasformazione lineare x → x+1. Legendre indicò anche il modo in cui applicare trasformazioni lineari per costruire polinomi generatori di secondo grado. Questi polinomi, che rappresentano numeri primi per un insieme di interi consecutivi, sono legati ai campi quadratici con numero di classe 1.

La distribuzione dei numeri primi

Legendre tentò anche di ricavare una formula asintotica per il numero π(x) di numeri primi non superiori a x, dove x è un numero reale, e dimostrò innanzitutto che non vi è alcuna espressione razionale per questo numero π(x). Tempo dopo, nel 1808, formulò l'ipotesi che π(x)≈x/(logx−a) con a=1,08366, ricavando questa espressione per 'induzione', vale a dire sperimentalmente. A partire dal 1792, anche Gauss si spinse a calcolare fino a x=3.000.000, e in una lettera a Johann Franz Encke del 1849 concluse che (teorema 3.1):

Questa ipotesi, nota ora come il 'teorema dei numeri primi', fu dimostrata per la prima volta, indipendentemente, da Jacques Hadamard e da Charles-Jean de La Vallée-Poussin nel 1896 con metodi analitici, ossia dimostrando per la funzione zeta

che ζ(s)≠0, se r=1. Quest'ultima affermazione è in effetti equivalente al teorema dei numeri primi. Una dimostrazione elementare di questo teorema (senza utilizzare metodi analitici) fu trovata indipendentemente da Atle Selberg e Paul Erdös nel 1949. Anche Gauss fornì, in un manoscritto del 1796, una formula empirica per il numero π₂(x) di numeri naturali minori di x che sono il prodotto di due diversi numeri primi, e cioè

La congettura di Goldbach

In una lettera a Euler del 7 giugno 1742, Christian Goldbach (1690-1764) formulò la seguente congettura (congettura 3.2): (1) ogni numero naturale pari m≥4 è la somma di due numeri primi dispari; (2) ogni numero naturale m>1 è la somma di tre (al massimo) numeri primi; (3) ogni numero naturale dispari m>1 o è un numero primo o è la somma di tre numeri primi dispari.

Naturalmente, la seconda e la terza affermazione derivano dalla prima. In precedenza, in un manoscritto non pubblicato (lo fu soltanto nel 1908 a opera di Paul Tannery), Descartes aveva affermato che ogni numero pari è la somma al massimo di tre numeri primi. Anche Edward Waring, nelle Meditationes algebraicae (1770) formulò un'ipotesi simile a quella di Goldbach. Nella sua risposta a Goldbach, Euler disse di credere fermamente nella sua validità, ma di non sapere come dimostrarla. In effetti non si ha tuttora una dimostrazione dell'ipotesi di Goldbach, sebbene da allora siano stati sviluppati metodi nuovi, come quello del cerchio, e siano stati ottenuti, nel XX sec., alcuni risultati parziali da parte di Hardy e Littlewood (1919 ca.), Brun (1920), Vinogradov (1937), Hua, Chen (1966) e altri.

Campi quadratici algebrici

Forme quadratiche: numeri primi rappresentati da forme quadratiche

Un altro tema che ebbe grande rilevanza nel XVIII sec. riguardava la possibilità che una data espressione quadratica ax²+bxy+cy²+dx+ey+f, con a, b, c, d, e, f interi, rappresentasse un dato intero m per certi valori interi di x e y, ossia che l'equazione ax²+bxy+cy²+dx+ey+f =m avesse una soluzione intera x, y ∈ ℤ; questo problema avrebbe portato poi, alla fine del XIX sec., alla creazione della 'teoria del campo di classi'. L'origine del problema è di natura chiaramente geometrica, essendo legata al teorema di Pitagora sui triangoli rettangoli. Appare per la prima volta in forma aritmetica nel libro Arithmetica di Diofanto, in cui si afferma che (teorema 4.1): un intero m della forma m=4t+3 non può essere la somma di due quadrati di interi, cioè m≠x²+y² per qualunque x, y ∈ ℤ.

Nel libro di Diofanto questo teorema non è dimostrato, ma una dimostrazione si può facilmente ricavare dalla teoria dei numeri pari e dispari (congruenza modulo 4) sviluppata dagli appartenenti alla scuola di Pitagora nel VI sec. a.C.

Il problema fu ripreso intorno al 1638 da Pierre de Fermat, dopo aver attentamente studiato l'edizione di Bachet del 1621 della Arithmetica di Diofanto. In una lettera a Mersenne del 1640 Fermat scriveva (teorema 4.2): un numero primo p≠2 è la somma di due quadrati, p=x²+y², con x e y numeri naturali, se e solo se p è della forma p=4t+1 (dove t è un numero naturale), cioè se e solo se p≡1 (mod 4). Questa rappresentazione inoltre è unica, per cui necessariamente x e y devono essere primi tra loro; in simboli (x,y)=1.

Tale osservazione diede luogo a descrizioni simili in termini dei resti (congruenze) rispetto all'intero 4N per numeri primi rappresentabili come p=x²+Ny², nei casi in cui N=−1, 2, −2, 3, 5. Ciò significa che i numeri primi così rappresentati devono essere contenuti in specifiche classi di congruenza r modulo 4N. Per esempio (teorema 4.3):

1) se N=2, r=1, 3;

2) se N=3, r=1, 7.

Ciò significa che, per il punto (1), un numero primo p≠2 è rappresentabile nella forma p=x²+2y², per x e y numeri naturali, se e solo se p≡1, 3 (mod 8); per il punto (2), un numero primo p≠2, 3 è rappresentabile nella forma p=x²+3y², per x e y numeri naturali, se e solo se p≡1, 7 (mod 12).

Il teorema 4.2 fu dimostrato da Euler negli anni 1747, 1752 e 1754. Per quanto riguarda il teorema 4.3, anch'esso fu all'inizio formulato da Fermat, ma dimostrato molto più tardi da Euler, nel 1756, 1760 e 1773, a eccezione del caso N=2 e r=3, che fu completato da Lagrange nel 1775. Nel 1752 Euler scoprì e dimostrò anche l'inverso del teorema 4.2, e cioè (teorema 4.4): se un numero naturale dispari m>1 è rappresentabile in modo unico come somma di due interi non negativi x e y, m=x²+y², e se inoltre x e y sono primi tra loro, allora m è un numero primo.

Questo teorema fornisce un metodo efficiente per verificare se un dato numero m della forma 4t+1 è un numero primo. Criteri analoghi furono ricavati da Euler per altri numeri dispari m della forma m=x²+Ny², con N=2, 3, derivati dall'inverso del teorema 4.3. Euler fornì una dimostrazione di questo teorema inverso per N=2, e Lagrange (1775) ne propose una per N=3. Euler osservò inoltre che non tutte le forme x²+Ny², cioè non tutti i numeri naturali N, forniscono un tale criterio per stabilire se il numero è primo. I numeri N che danno luogo a un criterio di tal genere li chiamò 'numeri comodi', poiché essi forniscono un modo pratico per verificare se un dato numero è primo o meno. Euler riuscì a determinare 65 numeri di questo tipo; la sua lista di numeri comodi, compilata nel 1778 ma pubblicata soltanto dopo la sua morte, inizia con N=1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 13, 15, ... e finisce con N=1848. Non si sa ancora se la lista di Euler sia in effetti completa; sappiamo solamente che c'è al massimo un solo altro numero comodo mancante. Gauss nel 1801 fornì una caratterizzazione dei numeri comodi in termini del 'genere' delle forme quadratiche.

Forme quadratiche: teoria algebrica delle forme quadratiche

Lagrange fu il primo ad affrontare uno studio più sistematico delle forme quadratiche binarie f(x,y)=ax²+bxy+cy² e della rappresentazione f(x,y)=ax²+bxy+cy²=m per dati valori interi di a, b, c, m, e lo fece nel 1773 e nel 1775 in due lunghi lavori, Recherches d'arithmétique, in cui egli estendeva lo studio effettuato in precedenza da parte di Euler del caso più semplice

[11] ax²+cy²=m.

Lagrange notò innanzitutto che l'equazione ax²+bxy+cy²+ +dx+ey+f=m si può ridurre alla forma ax²+bxy+cy²=m mediante una trasformazione lineare. A questo seguì la scoperta fondamentale che una trasformazione lineare intera e invertibile delle variabili x e y,

dell'equazione

[13] f (x,y)=ax²+bxy+cy²=m,

genera una nuova equazione

[14] f'(x', y')=a'x'²+b'x'y'+c'y'²=m

dello stesso tipo, con nuovi valori interi a′, b′, c′. È dunque possibile ricavare in un sol colpo informazioni su un'intera classe di equazioni diofantee dello stesso tipo. Lagrange scoprì che l'invariante importante di queste classi di forme quadratiche binarie ax²+bxy+cy² equivalenti rispetto alle trasformazioni lineari intere invertibili, di cui sopra, identificate da (α,β,γ,δ) tali che αγ−βδ=±1, è il discriminante d definito da d=b²−4ac.

Una proprietà fondamentale della teoria di Lagrange è enunciata dal seguente teorema (teorema 4.5):

1) tutte le forme quadratiche binarie della stessa classe hanno il medesimo discriminante;

2) per ogni intero dato d, c'è soltanto un numero finito di classi che possiedono questo valore intero come discriminante.

Gauss perfezionò la teoria di Lagrange, e la sviluppò in forma sistematica, e da molti punti di vista definitiva, nelle sue Disquisitiones arithmeticae.

Legge di reciprocità dei residui quadratici: Euler

A partire dal 1741, lo studio delle forme quadratiche e l'ispirazione tratta dalle ricerche di Fermat sui numeri primi p rappresentabili nella forma x²+Ny², con N=1, ±2, 3 e con valori interi x, y ∈ ℤ, condussero Euler a una delle sue scoperte più importanti (1772), la 'legge di reciprocità dei residui quadratici' (termine coniato da Legendre nel 1798). Questa legge va considerata come il teorema fondamentale sulle equazioni diofantee di grado 2, e afferma che (teorema 4.6): siano p, q due numeri primi dispari,

1) se p o q è della forma 4n+1, l'equazione x²+qy=p è risolubile con x, y interi se e solo se z²+pt=q è risolubile per z, t interi;

2) se p e q sono entrambi della forma 4n+3, l'equazione x²+qy=p è risolubile per x, y interi se e solo se z²+pt=q non è risolubile per z, t interi.

Questa legge fu formulata da Euler, inizialmente in forma implicita, nel lavoro dal titolo Theoremata circa divisores numerorum in hac forma paa±qbb contentorum (1744-1746 e 1751). In seguito, nel 1772, Euler ricavò una nuova forma, esplicita, della legge di reciprocità, pubblicata negli Euleri opuscula analytica 1 (1783) dopo la sua morte, e sotto il titolo Observationes circa divisionem quadratorum per numeros primos. Euler, tuttavia, afferma chiaramente negli Opuscula analytica di non essere in grado di dimostrare il teorema.

Legge di reciprocità dei residui quadratici: Legendre

Fu Legendre a riscoprire in modo indipendente questa legge nel 1785, dopo aver studiato le implicazioni del teorema di Fermat (teorema 2.1). Nello stesso anno Legendre iniziò a studiare il lavoro di Euler, e presentò negli scritti intitolati Recherches d'analyse indéterminée (1785) ed Essai sur la théorie des nombres (1798) la sua analisi della legge di reciprocità dei residui quadratici, e una dimostrazione parziale. La seconda opera citata rappresenta il primo libro in assoluto dedicato interamente alla teoria dei numeri. Nella seconda edizione del testo (1808) Legendre cita gli Opuscula analytica di Euler, ma non è chiaro se egli conoscesse la legge di reciprocità di Euler prima di quella data.

La dimostrazione di Legendre si basa sul seguente lemma, che risale a Euler (Opuscula analytica 1), e che giocò in seguito un ruolo chiave nella scoperta, nel 1923, del 'principio locale-globale' da parte di Helmut Hasse (teorema 4.7): siano a,b,c ∈ ℤ numeri interi non tutti dello stesso segno, e tali che abc sia un numero la cui scomposizione in fattori primi non contenga alcun fattore ripetuto. Allora l'equazione ax²+by²+cz²=0 possiede una soluzione non banale x,y,z ∈ ℤ se e solo se sono simultaneamente soddisfatte le seguenti condizioni:

a) −bc è un residuo quadratico modulo ∣ a ∣

b) − ca è un residuo quadratico modulo ∣ b ∣

c) − ab è un residuo quadratico modulo ∣ c ∣.

Un altro elemento di cui Legendre aveva bisogno per la sua dimostrazione è la seguente conseguenza del teorema di Fermat (teorema 2.1), il quale affermando che a^p−1≡1 (mod p) per p≠2 numero primo e a intero non divisibile per p, implica che a^(p−1)/2≡±1 (mod p). Sulla base di questa conseguenza, Legendre introdusse nel 1798 il cosiddetto 'simbolo di Legendre' (a/p) nel modo seguente: se p≠2 è un numero primo, e a è un intero non divisibile per p,

in cui il segno è definito in modo tale che

Legendre dimostrò che questo simbolo è ben definito e che è moltiplicativo, proprietà questa già notata da Euler. L'importanza di questo simbolo scaturisce dalla seguente osservazione chiave, fatta anch'essa già da Euler nei suoi Opuscula analytica 1 (teorema 4.8): se p≠2 è un numero primo, e a è un intero non divisibile per p, allora p divide x²−a per un x intero, se e solo se p divide a^(p−1)/2 −1; detto diversamente secondo la terminologia moderna, la congruenza x²≡a (mod p) è risolubile per un x intero se e solo se a^(p−1)/2≡+1 (mod p). Tale numero a si dice 'residuo quadratico' modulo p.

Questo non è altro che il criterio del residuo di Euler (teorema 2.7) per la potenza n=2. Utilizzando questo nuovo simbolo, la legge di reciprocità dei residui quadratici assume la forma seguente (teorema 4.9): siano p, q due numeri primi dispari,

1) se p o q è della forma 4n+1, allora (q/p)=(p/q);

2) se p e q sono entrambi della forma 4n+3, allora (q/p)=−(p/q).

Legendre proseguì quindi nella dimostrazione della legge di reciprocità, distinguendo otto casi a seconda delle condizioni p,q≡±1 (mod 4) e (q/p)=±1. Servendosi del teorema 4.7 dedusse quindi il segno di (p/q), dato quello di (q/p). La sua dimostrazione era però completa soltanto in due degli otto casi; per gli altri Legendre utilizzò una congettura che fu dimostrata solamente più tardi, nel 1837 da Dirichlet, e cioè che ogni progressione aritmetica contiene un numero infinito di numeri primi. Una prima dimostrazione completa della legge di reciprocità fu fornita da Gauss nelle sue Disquisitiones arithmeticae nel 1801, sebbene egli l'avesse scoperta già nel 1796, quando aveva 19 anni.

L'equazione di Pell

Un tipo particolare, ma importante, di equazione diofantea di secondo grado è quella che Euler, per ragioni ignote, chiamò 'equazione di Pell', sebbene John Pell (1611-1685) non abbia avuto con essa nulla a che fare, a parte il fatto di aver commentato un libro di algebra del matematico svizzero Johann Heinrich Rahn in cui compariva questa equazione (1659). Essa è presente comunque già nell'Arithmetica di Diofanto (V.9 e V.11). Alcune proprietà di questa equazione, cioè y²−ax²=1 con a intero positivo e non quadrato perfetto, erano state scoperte prima di Euler dagli indiani Brahmagupta (598-665?) e Bhāskara II (1114-1185?), e altre furono scoperte dopo Euler da Lagrange.

A partire dal 1730, Euler comprese che l'equazione diofantea y²=ax²+bx+c, con a, b, c coefficienti interi, possiede un numero infinito di soluzioni intere (x,y) se, oltre a possedere essa stessa soluzioni, anche l'equazione di Pell y²−ax² =1 ammette una soluzione. Osservò anche che le soluzioni (x_n,y_n) soddisfano una relazione di ricorrenza x_n=rx_n−1+sx_n−2, e che esse si possono esprimere esplicitamente in termini di √a, cioè come espressioni razionali nel campo quadratico ℚ(√a) (formule di Binet). La scoperta principale compiuta a questo proposito da Euler (1759) consiste nell'aver stabilito una connessione tra l'equazione di Pell e l'algoritmo delle frazioni continue, e cioè con lo sviluppo di √a in frazione continua. Sulla base di questa interpretazione Lagrange nel 1768 riuscì a dimostrare che l'equazione di Pell y²=ax²+1 possiede sempre una soluzione, e risolse quindi completamente il problema. Le principali proprietà dell'equazione di Pell si possono dunque enunciare nel modo seguente (teorema 5.1):

1) l'equazione di Pell y²−ax²=1, con a numero positivo, intero e non quadrato perfetto, possiede un numero infinito di soluzioni intere (x,y);

2) una 'soluzione particolare' è data dall'algoritmo delle frazioni continue applicato a √a;

3) l'insieme di 'tutte le soluzioni' si ottiene dalla soluzione 'più piccola' attraverso una legge di composizione razionale.

In termini moderni: i punti interi sull'iperbole y²−ax²=1 formano un gruppo (ciclico) generato da una soluzione particolare fondamentale (x,y), corrispondente all'unità fondamentale del campo ℚ(√a). La legge di composizione (razionale)

[17] (y²-ax²)(t²-az²)=(yt±axz)²-a(yz±xt)²,

scoperta da Euler intorno al 1753 e pubblicata nel 1764, ma già nota a Brahmagupta e a Bhāskara, corrisponde alla legge moltiplicativa per i numeri nel campo quadratico ℚ(√a).

Le frazioni continue

Le frazioni continue si ottengono iterando all'infinito l'algoritmo di divisione di Euclide. Esse furono inizialmente applicate come tali dal matematico indiano Āryabhaṭa I (476-?), per risolvere le equazioni diofantee lineari. Il primo ad applicarle per approssimare le radici quadrate come √2 fu Raffaele Bombelli nella sua opera L'algebra parte maggiore dell'aritmetica (1572). Ulteriori studi sulle frazioni continue furono portati avanti da John Wallis, nel 1655 e nel 1695, e da William Brouncker, che sviluppò 4/π in frazione continua. Dal 1731 Euler iniziò a studiare questo argomento, in relazione inizialmente con l'equazione differenziale di Jacopo Riccati, e in seguito con la teoria dei numeri. Nel suo primo lavoro sulle frazioni continue, De fractionibus continuis (1737), Euler dimostrò che ogni numero razionale si può scrivere come frazione continua 'finita', e che (teorema 6.1): uno sviluppo periodico in frazioni continue rappresenta un numero quadratico irrazionale α=a+b √d, con a, b, d numeri razionali e d non quadrato perfetto.

Euler notò anche che lo sviluppo in frazioni continue di qualunque numero reale β fornisce la migliore approssimazione razionale di β.

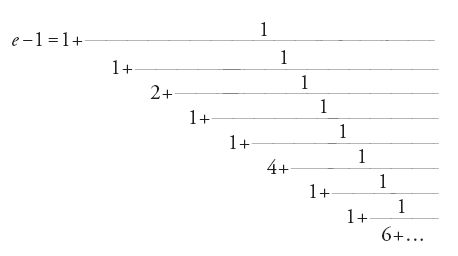
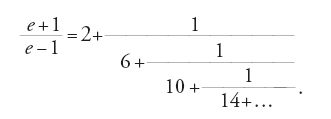
Nel suo lavoro e nel libro Introductio in analysin infinitorum (1748) Euler dedusse molti sviluppi in frazioni continue, come per esempio (teorema 6.2):

Il primo sviluppo, tuttavia, era stato trovato da Roger Cotes nel 1714. Fu proprio mediante questi sviluppi in frazioni continue che Euler riuscì a dimostrare essenzialmente che e ed e² sono irrazionali e sulla base del suo metodo, il matematico svizzero Johann Heinrich Lambert (1728-1777) dimostrò nel 1761 che π è irrazionale, derivando questo risultato dai seguenti due teoremi, entrambi da lui stesso dimostrati (teoremi 6.3 e 6.4):

1a) se x≠0 è un numero razionale, e^x è irrazionale, quindi,

1b) se e^x è un numero razionale, x deve essere irrazionale;

2a) se x≠0 è un numero razionale, tanx è irrazionale, quindi,

2b) se tanx è un numero razionale, x è irrazionale.

Si deduce pertanto che π è irrazionale, poiché tan(π/4)=1 è razionale.

Lambert dimostrò anche che lo sviluppo di tanx in frazione continua è convergente, che lo stesso vale per altre funzioni trascendenti, come log(1+x) e arctanx, e che ciò si verifica anche in casi in cui lo sviluppo in serie di potenze della funzione non converge.

Nel 1768 Lagrange dimostrò infine l'inverso del teorema 6.1 di Euler, e cioè (teorema 6.5): una radice irrazionale α di un'equazione quadratica, α=a+b√d, con a, b, d razionali e d non quadrato perfetto, possiede uno sviluppo periodico in frazione continua.

Somme di quadrati

Somma di quattro quadrati

Un altro contributo importante di Lagrange fu la dimostrazione, nel 1770, di un'antica congettura che risaliva a Diofanto (teorema 7.1): qualunque intero positivo m è la somma di al massimo quattro quadrati, m=x²+y²+z²+t², con x, y, z, t interi.

Bachet, nel Commentario (1621) alla Arithmetica di Diofanto, aveva verificato questa congettura fino a m=325, ma non fu in grado di dimostrarla, non più di Descartes, che (1638, lettere a Mersenne) lavorò sul problema dopo di lui. Fermat, in una lettera a Pascal, nel 1654, formulò una serie di congetture sulle somme di due quadrati, per mezzo delle quali, secondo lui, poteva dimostrare il teorema. A partire dal 1730 alcune di queste congetture furono dimostrate da Euler, il quale tuttavia poté (nel 1751) dimostrare la congettura in questione soltanto per valori razionali di x, y, z, t. Nel 1748, però, Euler scoprì la formula prodotto per la somma di quattro quadrati, che consentì in seguito a William Rowan Hamilton d'introdurre la moltiplicazione per i quaternioni. Fu Lagrange, alla fine, che riuscì a dimostrare il teorema per gli interi, seguendo le idee di Euler. Quest'ultimo due anni dopo, nel 1772, semplificò considerevolmente la dimostrazione di Lagrange.

Somma di tre quadrati

Adrien-Marie Legendre formulò in modo più preciso il teorema dei quattro quadrati, dimostrando nel 1785 e nel 1798 che (teorema 7.2): un intero positivo m è la somma di tre quadrati al massimo, m=x²+y²+z², con x, y, z interi, se e solo se m≠4^r(8t+7) per interi positivi qualunque r e t.

Parte di questo teorema era stata ipotizzata da Fermat in una lettera a Mersenne nel 1636, e cioè il fatto che un intero della forma (8t+7) non potesse essere la somma di tre quadrati di numeri razionali. Questo fu provato, inoltre, da Descartes, in una lettera a Mersenne del 1638, per numeri interi, dimostrando che il quadrato di un numero intero è necessariamente della forma 4t o della forma 8t+1. Altri risultati parziali erano stati ottenuti anche da Euler (come dimostra la corrispondenza con Goldbach).

Teoria analitica dei numeri

La funzione ζ di Euler: precursori di Euler

Già Nicola Oresme, intorno al 1360, operava una distinzione, nel suo trattato Quaestiones super geometriam Euclidis, tra alcune serie convergenti e altre divergenti, fornendo un criterio di convergenza o divergenza che egli utilizzò, tra l'altro, per accertare che la serie armonica è divergente, cioè (teorema 8.1):

è divergente.

Pietro Mengoli (1625-1686), proseguendo il lavoro di Pietro Antonio Cataldi nelle Novae quadraturae arithmeticae, pubblicate nel 1650, in cui si occupava di algoritmi infiniti e di serie infinite, dimostrò di nuovo il teorema. Formulò quindi il problema: dimostrare che

ha un valore finito v, e determinare questo valore. Valori approssimati per v=ζ(2) furono dati da John Wallis, nella sua Arithmetica infinitorum, nel 1655, da Daniel Bernoulli (1700-1782) in una lettera a Goldbach del 1728, da Christian Goldbach nella sua risposta a Daniel Bernoulli dello stesso anno, da James Stirling (1692-1770) nel 1720, e da Euler nel suo lavoro De summatione innumerabilium progressionum del 1731 e, con maggior precisione, nella Inventio summae cuiusque seriei ex dato termino generali del 1736. Alla fine fu Euler che riuscì a dare il valore esplicito v=ζ(2) nel lavoro De summis serierum reciprocarum del 1734-1735, che contribuì a consolidare molto presto la sua fama (teorema 8.2):

La funzione ζ di Euler: Euler

Euler introdusse la funzione ζ nel 1737 nel suo lavoro Variae observationes circa series infinitas, pubblicato nel 1744, come:

La ζ(k) per k ∈ ℕ, k≥2 era stata già considerata da Jakob I Bernoulli (1654-1705), il quale dimostrò che:

Nel 1737 Euler ne determinò una formulazione in termini di prodotto infinito (teorema 8.3):

(su tutti i primi p), s ∈ ℝ, s>1.

Questa identità si ricava per mezzo del teorema fondamentale dell'aritmetica, il quale afferma che qualunque numero naturale m>1 si può fattorizzare in modo unico in numeri primi (teorema dimostrato in seguito da Gauss nelle sue Disquisitiones arithmeticae). Il teorema 8.3 implica l'esistenza di un numero infinito di numeri primi; Euler, tuttavia, applicando il logaritmo al prodotto infinito, ricavò un risultato molto più forte, dimostrando che

è divergente, cioè (teorema 8.4):

effettuando la somma su tutti i numeri primi p.

Dopo aver calcolato nel 1735 ζ(2k), con k numero naturale, Euler scoprì nel 1739 la relazione con i numeri di Bernoulli (teorema 8.5):

in cui i numeri di Bernoulli B_2k erano stati definiti da Euler come i coefficienti della serie seguente:

Dunque,

(con B_k=0, se k è un numero naturale dispari e k>2) e quindi:

I numeri di Bernoulli sono numeri razionali, e furono introdotti da Jakob I Bernoulli nel suo libro sulla probabilità Ars conjectandi, pubblicato postumo nel 1713. Euler calcolò anche, nel 1735, ζ(2k+1) per k ∈ ℕ, cioè la ζ per i numeri naturali dispari, ma non riuscì a determinare una formula esplicita. Nel 1749 però egli scoprì la cosiddetta 'equazione funzionale' (teorema 8.6):

Questa equazione fondamentale fu dimostrata nel 1859 da Bernhard Riemann (1826-1866), che introdusse la ζ(s) come funzione complessa, s ∈ ℂ, e dimostrò che è possibile estendere ζ(s) all'intero piano complesso ℂ, e che ζ(s) è una funzione meromorfa con un solo polo in s=1, il quale è un polo semplice con residuo 1.

Curve di 'genere' superiore

L'ultimo teorema di Fermat

Fermat, scrivendo a Pierre de Carcavy, fornì alcune indicazioni sul modo per dimostrare la sua seguente osservazione (teorema 9.1): l'equazione diofantea di quarto grado x⁴+y⁴=z⁴, non ha soluzione per interi x, y, z non nulli.

Lo studio, da parte di Fermat, di questa equazione diofantea fu motivato senza dubbio da un teorema contenuto negli Elementi di Euclide (Libro X, prop. 28, lemma 1). Esso enunciava una proprietà già nota ai Babilonesi intorno al 1700 a.C. (teorema 9.2): l'equazione diofantea x²+y²=z² possiede un numero infinito di soluzioni non nulle e intere x, y, z, e le soluzioni possono essere tutte rappresentate mediante due parametri interi u e v.

Tenendo conto di questa osservazione, Fermat ipotizzò che in generale (congettura di Fermat 9.3): l'equazione diofantea xⁿ+yⁿ=zⁿ, non possiede soluzioni intere non nulle x, y, z per n>2.

Euler, nel 1753, fornì una dimostrazione della congettura di Fermat per l'esponente n=3. La sua dimostrazione utilizzava implicitamente l'aritmetica del campo ciclotomico delle radici cubiche dell'unità

preparando in tal modo il terreno allo studio dell'aritmetica dei numeri algebrici. Per l'esponente n=5 Legendre e Dirichlet riuscirono a dimostrare la congettura di Fermat nel 1825, e la sua validità per il caso n=7 fu stabilita da Gabriel Lamé nel 1839. La congettura, tuttavia, è stata dimostrata completamente soltanto di recente da Andrew Wiles (1995), provando la validità della congettura di Eichler-Shimura-Taniyama sulla modularità delle curve ellittiche, e utilizzando risultati ottenuti da diversi matematici.

La teoria additiva dei numeri

La teoria additiva dei numeri studia problemi legati a tipi particolari di equazioni diofantee, quali, per esempio, la scrittura di un dato numero intero m come somma di un certo tipo di numeri interi.

Partizioni

Fu ancora Euler che, stimolato da alcune domande che gli erano state poste da Philippe Naudé in una lettera del 1740, esaminò per primo in maniera sistematica il numero di modi nel quale un dato numero naturale m si può scrivere come s(m) somma di numeri naturali non crescenti, per esempio 5=4+1=3+2=3+1+1=2+2+1=2+1+1+1=1+1+1+1+1.

Si ha dunque che: s(1)=1, s(2)=2, s(5)=7, ecc. All'origine di questa teoria delle partizioni vi è il lavoro di Euler dal titolo Observationes analyticae variae de combinationibus (1741), nel quale venivano introdotti per la prima volta determinati strumenti analitici allo scopo di affrontare problemi di teoria dei numeri. L'argomento fu ripreso in maggior dettaglio nel capitolo XVI della Introductio in analysin infinitorum di Euler (pubblicata nel 1748, ma scritta nel 1744), e nel lungo lavoro intitolato De partitione numerorum (1750, continuato nel 1768). Questi scritti prepararono il terreno a branche importanti della teoria analitica dei numeri, come il metodo del cerchio di Hardy, Littlewood e Ramanujan (1918), la funzione eta di Julius Wilhelm Richard Dedekind (1877) e l'applicazione delle funzioni ellittiche alla teoria dei numeri (da parte, per es., di Carl Gustav Jacob Jacobi, a cominciare dal 1828). Leibniz, in una lettera destinata a Johann Bernoulli, si era già espresso in merito alla rilevanza del problema, essendo questo connesso alla determinazione del numero di funzioni simmetriche di grado dato. Euler trovò un numero sorprendente di identità legate a s(m); tra queste, è fondamentale la seguente rappresentazione prodotto della cosiddetta 'funzione generatrice'

della funzione di partizione s(m), e cioè (teorema 10.1):

Questa identità fu utilizzata successivamente da Hardy e Ramanujan (1918) per determinare un'espressione asintotica di s(m).

Servendosi della funzione inversa della S(x), Euler scoprì una relazione ricorsiva per s(m), che gli consentì di calcolare i valori s(m) in successione, a partire da s(1)=1. Nel lavoro del 1768 egli sviluppò anche alcuni metodi analitici per dimostrare una congettura formulata da Fermat in una lettera a Mersenne del settembre 1636, e cioè (teorema 10.2) che:

1) ogni numero naturale m è la somma di tre numeri triangolari;

2) ogni numero naturale m è la somma di quattro numeri quadrati;

3) ogni numero naturale m è la somma di cinque numeri pentagonali;

4) ogni numero naturale m è la somma di n numeri ennagonali.

La seconda affermazione, però, fu dimostrata soltanto nel 1770 da Lagrange, la prima da Legendre nel 1798 e da Gauss nelle sue Disquisitiones arithmeticae (art. 293), mentre la quarta (e quindi anche la terza) da Cauchy tra il 1813 e il 1815. Il lavoro di Euler del 1741 contiene, proprio alla fine, un primo esempio di serie θ (teorema 10.3):

Euler notò immediatamente che gli esponenti di questa se-

rie contengono i numeri pentagonali n=1/2 k(3k±1), prendendo il segno positivo per k pari e il segno negativo per k dispari. Euler scoprì in tal modo essenzialmente la formula prodotto per la forma modulare:

Il teorema 10.3 fu dimostrato da Euler per la prima volta in una lettera indirizzata a Goldbach, il 29 maggio del 1750. Successivamente, ispirandosi a questa idea di Euler sulle serie con esponenti appartenenti a una progressione aritmetica del secondo ordine, Jacobi avrebbe costruito la sua teoria delle funzioni ellittiche. Un'altra notevole proprietà di questo tipo, dimostrata da Euler, è la rappresentazione (teorema 10.4):

Euler si occupò anche di molte altre funzioni aritmetiche, come il numero q(m) di rappresentazioni di un numero naturale m come somma di numeri naturali diversi, oppure il numero u(m) di rappresentazioni di m come somma di numeri naturali dispari.

Il problema di Waring

Edward Waring (1734-1798) formulò nelle Meditationes arithmeticae il teorema noto oggi come 'teorema di Waring', cioè (teorema 10.5):

1) ogni numero naturale m è la somma di al più 9 cubi (non negativi);

2) ogni numero naturale m è la somma di al più 19 potenze quarte;

3) per ogni potenza n>1 esiste un numero (minimo) k=k(n) tale che ogni numero naturale m è la somma di al più k potenze n-esime non negative.

Secondo i teoremi di Lagrange (teorema 7.1) e Legendre (teorema 7.2) il minimo numero k per la potenza n=2 è k(2)=4. Waring non riuscì a verificare il suo teorema, e fu David Hilbert che, nel 1909, dimostrò la proposizione 3.

Wieferich (1909) e Kempner (1912) hanno dimostrato che k(3)=9, e soltanto recentemente, nel 1987, Balasubrama niam, Dress e Deshouillers hanno verificato che k(4)=19. Chen ha inoltre dimostrato nel 1964 che k(5)=37, e Pillai, nel 1935, che k(6)=73.