L'Universo matematico
Frontiere della Vita (1998)
L'Universo matematico
Parte di questo saggio è stata pubblicata sotto il titolo Perché il mondo è matematico? Roma-Bari, Laterza, 1992
La matematica è lo strumento principale dello scienziato. Essa è miracolosamente efficace nel descrivere e predire il comportamento della natura. Ma che cos'è la matematica, e perché il mondo è matematico? Descriveremo alcune diverse concezioni della matematica ed esamineremo le risposte che esse danno alla domanda circa la sua utilità. Le idee moderne sulla computabilità e sugli algoritmi di compressione permettono di trattare questi problemi in un modo nuovo. II nostro Universo fisico è estremamente comprimibile, e un numero relativamente limitato di semplici funzioni computabili ci permette di descrivere quasi tutto ciò che incontriamo in esso. È comprensibile che l'Universo possa essere descritto mediante la matematica, ma è misterioso il fatto che la matematica necessaria sia relativamente semplice.
Introduzione
Esistono molte concezioni filosofiche sulla natura, sull'acquisizione della conoscenza umana in generale e di quella matematica in particolare. In primo luogo c'è l'empirismo, secondo cui tutta la nostra conoscenza viene acquisita a partire dall' esperienza. Per gli empiristi non esistono verità necessarie. C'è poi l'idealismo, i cui sostenitori credono nell'esistenza di un mondo esterno alle nostre menti, nel quale le cose esistono indipendentemente dal pensiero. Per gli idealisti la conoscenza è il prodotto di un processo di scoperta. Entrambi questi punti di vista sono antichi; di recente, si è aggiunto alla lista l'operazionismo, che ha goduto di grande popolarità nei primi anni di questo secolo. La filosofia operazionista tenta di definire il significato delle cose tramite la successione dei passaggi, o operazioni, che dovrebbero essere eseguite per misurarle. C'è infine la tradizione del logicismo, che cerca di codificare tutto il nostro sapere in un sistema di assiomi e di regole di inferenza, e che definisce la conoscenza come l'insieme di tutti i possibili sistemi deduttivi logicamente coerenti.
A ciascuna di queste grandiose concezioni corrisponde una spiegazione per il mondo della matematica. Dal campo empirista emerge l'idea dell'invenzionismo, secondo cui la matematica è semplicemente ciò che i matematici fanno. Si tratta di un'invenzione della mente umana adatta a particolari scopi che possono essere pratici o estetici. Entità matematiche come gli insiemi o i triangoli non esisterebbero se non ci fossero i matematici. La matematica la inventiamo, non la scopriamo. Secondo questo punto di vista, la ragione per cui la troviamo così utile è che l'abbiamo costruita proprio per questo scopo; addirittura, l'utilità della matematica potrebbe essere un riflesso di quanto poco conosciamo del mondo, in quanto i suoi aspetti matematici sono gli unici che siamo stati in grado di scoprire sistematicamente. Questa visione è comune tra i 'consumatori' di matematica coloro che si occupano di scienze sociali o di economia, per esempio - piuttosto che tra i matematici stessi. La sua influenza si vede nel proliferare di testi con titoli del tipo Modelli matematici dei fenomeni sonori, mentre un centinaio di anni fa, per pubblicizzare la completezza e l'unicità, sarebbe stato più appropriato un titolo come La teoria del suono. Questa enfasi moderna sul ruolo giocato dall'intervento umano è strettamente associata al punto di vista della filosofia kantiana secondo cui, sebbene possa esistere una qualche realtà ultima, noi non possiamo conoscerla se non filtrando le nostre osservazioni e l'esperienza che abbiamo di quella realtà attraverso le categorie mentali che la ordinano, affrnché la si possa comprendere. Così, anche se l'Universo ci appare matematico, ciò non significa che lo sia realmente, non più di quanto sia rosa il cielo dato che esso ci appare tale quando portiamo occhiali dalle lenti rosa.
La matematica: un'invenzione umana?
Se la matematica fosse esclusivamente un'invenzione umana e fosse usata dagli scienziati solo perché è utile e disponibile, allora ci potremmo aspettare che essa manifesti al suo interno differenze culturali significative. Invece, sebbene ci siano stili diversi nella presentazione dei concetti matematici e nel tipo di matematica studiata nelle differenti culture, si tratta solo di differenze superficiali. La scoperta degli stessi teoremi matematici, fatta in maniera indipendente da persone con un retroterra economico, culturale e politico completamente diverso, e in momenti storici diversi, rappresenta un buon argomento contro questo modo semplicistico di vedere le cose. Inoltre il fenomeno delle ripetute invenzioni indipendenti delle stesse verità matematiche, inusuale in altre discipline, rende la matematica creativa diversa dalla musica e dall'arte. Il teorema di Pitagora è stato scoperto molte volte indipendentemente da pensatori diversi e questo fatto suggerisce che i fondamenti della matematica posseggano un elemento che si trova al di fuori della mente umana e che non è completamente modellabile dal nostro modo di pensare: una parte della matematica viene scoperta.
l seguaci di questo approccio minimalista al problema dell' efficacia della matematica potrebbero tentare di fare un passo ulteriore rispetto alla posizione di Kant e sostenere che, anche se noi possiamo avere delle categorie mentali che filtrano la nostra conoscenza grezza del mondo, esse comunque di storcono la realtà in maniera trascurabile. Infatti, le nostre facoltà mentali sono il risultato di un processo di selezione naturale che ha generato quelle rappresentazioni che sono le più fedeli alla vera natura del mondo esterno. l nostri occhi ci comunicano la vera natura della luce; le nostre orecchie quella del suono. Se le nostre menti avessero prodotto rappresentazioni del mondo che si discostavano significativamente dalla natura vera delle cose, quelle rappresentazioni avrebbero avuto un valore di sopravvivenza minore rispetto a rappresentazioni più fedeli della realtà. In effetti questa argomentazione non solo ci rassicura sul fatto che le distorsioni mentali dovute alle categorie kantiane sono trascurabili, ma spiega anche l'origine di quelle categorie e perché esse siano condivise da menti umane differenti. Questo approccio realista e diretto alle cose nasconde, però, un problema. Tale teoria, infatti, sembra garantire che la nostra concezione del mondo (aspetti matematici e tutto il resto) sia accurata, dato che una rappresentazione accurata è necessaria alla nostra sopravvivenza nel corso dell'evoluzione, ma non c'è ragione per cui dovrebbero essere fedeli anche le rappresentazioni di quelle parti 'esoteriche' dell'Universo che non hanno giocato alcun ruolo nella nostra evoluzione. Eppure la matematica spesso si dimostra più affidabile ed efficace proprio in aree della scienza molto distanti da quelle che hanno avuto un ruolo nella nostra evoluzione. La correttezza delle nostre idee su questi fenomeni esoterici potrebbe essere spiegata se l'abilità di comprendere cose come la teoria quantistica, i buchi neri, la teoria della relatività, pur non avendo di per sé valore per la sopravvivenza, derivasse da una combinazione di molti passi logici elementari (come causa-effetto, contare, uguagliare, e così via), la cui conoscenza può realmente aver avuto un ruolo nella sopravvivenza. Quindi la nostra abilità nel comprendere la fisica matematica avanzata è solo un sottoprodotto di una moltitudine di altre semplici capacità che si sono sviluppate per il valore di sopravvivenza che esse avevano.
Il punto di vista logicistico è stato espresso nella fede verso il formalismo matematico, sviluppatasi verso la fine del diciannovesimo secolo. A quell' epoca i matematici si trovarono di fronte a vari problemi sconcertanti che avevano scosso la loro fiducia. Paradossi logici come quello proposto da Bertrand Russell: «Un barbiere rade tutti quelli che non si radono da soli. Chi rade il barbiere?»; il paradosso di Epimenide («questa proposizione è falsa») citato da Paolo nella lettera a Tito («tutti i cretesi sono bugiardi, lo ha detto uno dei loro poeti») o il dilemma «l'insieme di tutti gli insiemi che non contengono loro stessi (quest' insieme contiene se stesso?)» erano usati per mettere in difficoltà l'intero edificio matematico. Quindi, chi poteva prevedere da dove il prossimo paradosso sarebbe venuto fuori? Forse l'aritmetica stessa era infestata da paradossi sconosciuti o, ancora peggio, da incongruenze.
Il formalismo
Di fronte a questo dilemma David Hilbert, il più famoso matematico dell'epoca, propose di smettere di preoccuparsi del significato della matematica e, invece, di definire la matematica come l'insieme delle sequenze di formule che possono essere generate da un qualunque insieme di assiomi iniziali, manipolando i simboli in accordo con specifiche regole. Si pensava che questa procedura non avrebbe potuto generare o ammettere paradossi. La matematica è quindi quell'enorme trama di connessioni logiche che risulta dalla manipolazione di tutti i possibili assiomi iniziali consistenti, in accordo con tutti i possibili e noncontraddittori insiemi di regole. Questa visione della matematica è chiamata formalismo.
Chiaramente Hilbert e i suoi discepoli non cercavano di spiegare la miracolosa applicabilità della matematica alla natura. La matematica non possiede alcun significato in sé, e da questo punto di vista essa è in antitesi all'antico approccio mistico della numerologia; gli assiomi e le regole per la manipolazione dei simboli non sono connessi necessariamente alla realtà osservata. Le formule esistono su pezzi di carta, ma le entità matematiche che esse rappresentano non hanno nessuna pretesa di esistere. I formalisti non aspirano a offrire una spiegazione del carattere matematico della fisica più di quanto cerchino di spiegare perché i fenomeni fisici non osservino le regole del poker o degli scacchi.
Hilbert pensava che questa strategia, per definizione, avrebbe liberato la matematica da tutte le sue aree problematiche. Egli non voleva semplicemente bandire i paradossi logici, ma anche dimostrare l'autoconsistenza della matematica. Data una qualunque proposizione matematica, sarebbe stato possibile, in linea di principio, ripercorrendo il percorso logico delle connessioni tra gli assiomi e la proposizione in questione, determinare se essa fosse una conseguenza vera o falsa di qualunque particolare insieme di assiomi di partenza. Hilbert e i suoi discepoli cominciarono a lavorare, fiduciosi di poter confinare tutte le conseguenze di ogni proposizione matematica, nota e sconosciuta, entro questa 'camicia di forza'. Nel suo famoso discorso al congresso internazionale dei matematici tenuto si a Bologna nel 1900, Hilbert spiegò quali pensava fossero i più grandi problemi irrisolti della matematica; il suo Secondo Problema era niente di meno che "dimostrare la consistenza della aritmetica".
Hilbert stesso cominciò a cercare la dimostrazione. La sua strategia era chiara. Cominciò con sistemi logici semplicissimi, più piccoli dell'aritmetica (per esempio, l'aritmetica senza le operazioni di moltiplicazione e di divisione), e provò la loro consistenza mostrando che essi contengono necessariamente una proposizione che non può essere dimostrata. La proposizione usata era "0 = 1". Egli sfruttava il ben noto fatto che se un sistema logico contiene una proposizione falsa (e quindi è inconsistente), allora è possibile usarla per dimostrare la veridicità di ogni altra proposizione. Così, se c'è una qualche proposizione che non può essere dimostrata vera, allora non ci può essere alcuna inconsistenza logica. Quando, una volta, Bertrand Russell fece questa affermazione durante una conferenza pubblica, venne invitato da un ascoltatore scettico a dimostrare che l'interrogante era il papa, supposto che il doppio di due fosse uguale a cinque. Russell replicò senza esitazione che "se il doppio di due è cinque, allora quattro è uguale a cinque; sottraendo tre si ottiene che due è uguale a uno; ma lei e il papa siete due persone, quindi lei e il papa siete un tutt'uno".
Hilbert fece molti progressi con questo metodo; egli provò la consistenza di sistemi di assiomi sempre più grandi, tra cui la geometria euclidea, dimostrando fra l'altro quanto la scelta degli assiomi di Euclide fosse stata ispirata: essi erano sia consistenti sia logicamente indipendenti uno dall'altro. Hilbert pensava di riuscire ad aggiungere pochi altri assiomi per ampliare il sistema fino a includervi tutta l'aritmetica e completare la prova della sua consistenza senza complicazioni. Da questo programma di ricerca ci si aspettava la dimostrazione della consistenza degli assiomi dell'aritmetica e una procedura univoca per decidere la veridicità o la falsità di qualsiasi proposizione aritmetica.
Sfortunatamente, e in modo del tutto inaspettato, l'impresa crollò quasi da un giorno all'altro. Nel 1931 Kurt Gödel, un giovane matematico sconosciuto dell'università di Vienna, dimostrò che l'obiettivo di Hilbert non era raggiungibile. Qualunque insieme auto consistente di assiomi iniziali si scelga, quali che siano le regole adottate per manipolare i simboli matematici in questione, nel momento in cui il sistema è sufficientemente ampio da includere l'aritmetica, deve esistere almeno una proposizione che può essere formulata in quel linguaggio simbolico e la cui veridicità o falsità non può essere decisa usando quegli assiomi e quelle regole. La verità matematica è qualcosa che va al di là delle regole e degli assiomi. Il tentativo di risolvere il problema aggiungendo una nuova regola o un nuovo assioma non fa che generare una nuova proposizione indecidibile. Scacco matto: il programma di Hilbert non può funzionare. Se si vuole una piena comprensione di un sistema matematico bisogna uscire al di fuori di esso. Gödel arrivò a questa dimostrazione usando una versione nuova e sofisticata di una vecchia idea di Leibniz. Sviluppò un metodo non ambiguo per associare numeri a proposizioni, così che ogni proposizione sulla matematica fosse rappresentata in modo univoco da un numero (ora chiamato numero di Gödel), e viceversa, per ogni numero si potesse trovare la proposizione associata. Venne fatta una attenta distinzione tra gli enunciati matematici (cioè gli enunciati della matematica) e quelli meta-matematici (cioè gli enunciati sulla matematica). Per esempio "2 + 2 = 4" è una proposizione matematica, mentre "2 + 2 = 5 è falso" è una proposizione meta-matematica. Mediante il processo di attribuzione del numero di Gödel il giovane matematico austriaco stabilì una corrispondenza diretta tra l'aritmetica e le proposizioni sull'aritmetica. Supponiamo ora di considerare la seguente proposizione: "Il teorema il cui numero di Gödel è X è indecidibile". Il numero di Gödel della proposizione precedente, diciamo G, può essere calcolato. Se ora sostituiamo X con G nella proposizione precedente, abbiamo un teorema che prova la sua non-dimostrabilità! Gödel, quindi, aveva sfruttato l'esistenza dei famosi paradossi autoreferenziali in logica per dimostrare l'indecidibilità della aritmetica, usando la corrispondenza uno a uno tra la matematica e la meta-matematica originata dalla numerazione di Gödel. Il progetto di ricerca di Hilbert, e con esso la speranza di costringere la matematica nella camicia di forza del formalismo, fallì. Sistemi di assiomi sufficientemente ricchi da includere l'aritmetica sono necessariamente incompleti; ciò significa che esistono proposizioni dell' aritmetica che non possono essere né dimostrate né confutate usando gli assiomi e le regole della deduzione aritmetica. In seguito Gödel si spinse ancora oltre e provò che non si può dimostrare l'autoconsistenza di nessun sistema logico che contenga l'aritmetica. Solo se un sistema logico è più piccolo dell'aritmetica si può dimostrare che esso è consistente, e che tutte le sue proposizioni possono essere dimostrate vere o false. Questo è il caso della geometria euclidea: si può dimostrare che ogni sua proposizione è una conseguenza vera o falsa degli assiomi della teoria, sebbene la procedura necessaria possa essere in generale molto lunga.
La dimostrazione di Gödel dell 'impossibilità di evitare l'indecidibilità ha dato origine a molte applicazioni nelle aree più diverse del pensiero umano. Sono state fatte considerazioni sulle sue implicazioni nella possibilità di raggiungere una comprensione completa dell'Universo fisico usando gli strumenti della matematica; si è sostenuto che siccome noi possiamo 'vedere' la verità delle proposizioni di Gödel, ciò significa che la mente umana non può essere un sistema formale. Qualora ciò fosse vero, allora l'impresa di quegli studiosi dell'intelligenza artificiale che vorrebbero ridurre il funzionamento della mente umana a un singolo algoritmo, sarebbe senza speranza. Ecco un esempio di una semplicissima proposizione matematica nota per essere indecidibile. Si definisca grande un insieme di numeri che contiene più elementi del valore del suo elemento più piccolo. Se un insieme non è grande allora diremo che esso è piccolo. Per esempio {3, 6, 9, 46, 78} è un insieme grande, perché contiene più di tre elementi, mentre {21, 23, 45, 100} è piccolo perché contiene meno di ventuno elementi. Ora è noto che, se si prendono abbastanza numeri e li si suddividono in un modo qualsiasi in due gruppi, allora una parte costituirà sempre un insieme grande. Ma il problema di determinare a quanto corrisponda "abbastanza numeri" sarà indecidibile. Anche se non fosse stato dimostrato che gli obiettivi del formalismo sono irraggiungibili, tale filosofia della matematica sarebbe risultata insoddisfacente, perché qualsiasi proposizione è vera in un qualche sistema assiomatico. Inoltre, se allarghiamo il sistema in modo tale da includervi nuovi assiomi, dobbiamo considerare tutte le strutture a esso appartenenti come diverse da quelle appartenenti al sistema originario. Tecnicamente i triangoli del nuovo sistema non sarebbero gli stessi triangoli del sistema vecchio, eppure noi sentiamo che in un certo senso sono la stessa cosa. Ancora peggio: sappiamo che nessun formalismo coglie il lavoro effettivamente svolto da tutti i matematici.
Nonostante le 'falle' inaspettate del formalismo, questa dottrina non scomparve completamente. Molti matematici puri si accontentavano di andare avanti come al solito, senza preoccuparsi del fatto che l'aritmetica, o strutture logiche più sofisticate, potessero essere in realtà inconsistenti, essendo impossibile provare il contrario. L'aritmetica era sopravvissuta per millenni senza reali disastri e quindi i matematici erano felici di continuare nella pia speranza che nessuna inconsistenza sarebbe mai apparsa in futuro.
Una delle conseguenze di questo atteggiamento è stata che una versione ammorbidita del formalismo ha continuato a essere praticata, e può ancora essere ritrovata come una maniera di guardare alla matematica che evita il coinvolgimento nei problemi filosofici relativi al significato. Questo approccio attrae particolarmente coloro che sono interessati alle applicazioni, e che desiderano distinguere nettamente tra la matematica pura e quella applicata. Recentemente la bandiera del formalismo è stata portata soprattutto da quel consorzio di matematici francesi noto con lo pseudonimo di Nicolas Bourbaki, che negli ultimi cinquant'anni sono stati coautori di una serie di libri sulle strutture fondamentali della matematica, e in particolare della aritmetica e della geometria. Essi rappresentano l'ultima speranza dei formalisti: è la supremazia dell'assiomatica, del rigore e della sobria eleganza; si rifugge dai diagrammi, dagli esempi e dal particolare, a favore dell'astratto e del generale. Lo scopo del progetto Bourbaki non era quello di ottenere nuovi risultati, ma di codificare e unificare le cose note in un sistema astratto nuovo e più conciso.
Il progetto Bourbaki partì nel 1939 ed ebbe un retroscena divertente. Nessuno infatti sembra sapere perché il gruppo di matematici francesi che lo avviarono scelse lo pseudonimo di un francese inesistente. Forse furono ispirati dalla memoria del generale Charles Denis Sauter Bourbaki, un eccentrico ufficiale dell' esercito francese che si distinse nella guerra franco-prussiana e che pare avesse declinato l'offerta del trono di Grecia nel 1862. Dieci anni dopo la fortuna lo abbandonò e, insieme ai suoi soldati, lo ritroviamo imprigionato in Svizzera dove tentò di spararsi, ma senza riuscirci. C'è una sua statua nella città di Nancy e molti dei collaboratori al progetto Bourbaki furono legati all'Università di Nancy nei primi anni della loro carriera. Si raccontano molte altre storie strane circa il vero signor Bourbaki, molte delle quali probabilmente create dal gruppo stesso per rendere la leggenda più affascinante.
Nonostante i limiti posti dalla scoperta di Gödel, il gruppo Bourbaki voleva codificare la parte decidibile della matematica in maniera unificata, concentrandosi sulle differenti strutture algebriche che vengono generate dai diversi insiemi di assiomi e regole appropriati alle differenti aree della matematica. Bourbaki sperava di riuscire a organizzare le diverse parti della conoscenza matematica in un unico corpus, così da far emergere nuove similitudini tra strutture superficialmente diverse, e sfruttarle in tutto il campo degli studi. La matematica, per Bourbaki, è semplicemente il prodotto del lavoro dei matematici, "una creazione umana e non una rivelazione divina". La matematica è vista come una struttura vivente, in crescita, che richiede di essere organizzata se si vuole evitare che diventi caotica e frammentata.
Tuttavia, il programma del gruppo Bourbaki di organizzare la matematica entro una rete ordinata di connessioni logiche è sempre minato dalla mancanza di una qualunque prova di autoconsistenza. Questo spettro è affrontato in maniera pragmatica facendo appello all'esperienza e fidando nel fatto che la mancanza di tale prova è raramente importante e che, comunque, è innocua. È necessario solo vivere un po' pericolosamente. Ironicamente, nonostante il desiderio di separare la matematica da qualunque traccia di legame con il mondo reale, l'appello al mondo reale come una delle tante possibili strutture auto consistenti rende la matematica di Bourbaki, con la sua indimostrabile autoconsistenza, semplicemente una scienza come tutte le altre.
L'ostilità verso la filosofia del gruppo Bourbaki che spesso si trova tra coloro che praticano la matematica applicata (come Vladimir I. Amold) nasce dall'impressione che essa allontani la matematica dalla fisica, una connessione che è stata spesso ispiratrice di nuove idee. Nonostante ciò, l'influenza del progetto Bourbaki è stata molto grande. Negli anni Sessanta e Settanta sembra che sia stata di stimolo a quei programmi di insegnamento detti della nuova matematica, adottati nelle scuole superiori di molti paesi. Questo approccio all'insegnamento della matematica si discosta molto da quello tradizionale in cui l'enfasi è posta sulla manipolazione e sulla soluzione dei problemi. Nella nuova matematica, invece di aritmetica, interessi, logaritmi, geometria e calcolo, si studiano gli insiemi, i gruppi e altre strutture matematiche astratte. Questo esperimento sembra non aver avuto molto successo e l'attuale modello di insegnamento della matematica ai bambini è molto meno astratto. Molte delle proteste dei genitori contro la nuova matematica sono state causate senza dubbio dal fatto che essi si sentivano frustrati nel vedere che i loro figli non erano in grado di eseguire i calcoli matematici tradizionali con sufficiente abilità. E non essendo essi stessi in grado di capire le cose che venivano insegnate, i genitori non potevano offrire alcun aiuto ai loro figli.
Alla metà degli anni Ottanta un'indagine svolta tra i matematici attivi rivelò che il trenta per cento di loro era formalista nel senso di Bourbaki. Una spiegazione è che gran parte del lavoro matematico è ben lontano dall' essere lavoro di 'scoperta' come comunemente si crede; in questo lavoro prevale, piuttosto, un processo di affinamento, tramite cui dimostrazioni difficili e complicate vengono rese sempre più semplici e brevi, frnché si possa dichiarare che la successione di argomenti è ovvia o banale. Con banale i matematici intendono che non si fa appello ad argomenti nuovi: la dimostrazione è stata ridotta a una sequenza di operazioni note. Per realizzare questo scopo probabilmente è meglio agire da formalista, anche se si dovessero trovare poco attraenti alcune implicazioni di questa prospettiva filosofica.
Bourbaki inoltre deve rispondere alla domanda formulabile con le parole di Einstein: "Come è possibile che la matematica, la quale, dopo tutto, è un prodotto della mente umana indipendente dalla realtà, si adatti così bene agli oggetti della realtà?". l formalisti come Bourbaki vedono il lavoro dei matematici come una spiegazione delle strutture fondamentali della logica; se si va in profondità esse ingloberanno tutte le inter-relazioni logicamente ammissibili. Il mondo che ci circonda è visto come una realizzazione pratica di alcune di queste strutture, così che queste possano essere esemplificate o modellate dalle particolari inter-relazioni esistenti tra le cose materiali. Il fatto che le strutture formali della matematica non abbiano di per sé alcun significato può essere reinterpretato: invece di sostenere che non possono essere applicate a nulla, si può sostenere che esse si applicano a tutte le cose possibili. L'Universo osservato non è che una di esse.
Il platonismo
Il modo più semplice di considerare la matematica è sostenere che il mondo è matematico in un qualche senso profondo. l concetti matematici esistono e sono scoperti dai matematici, non sono inventati. 7r è realmente nel cielo e la matematica esiste, che ci siano o meno i matematici. È un linguaggio universale che potrebbe essere usato per comunicare con esseri di altri pianeti sviluppatisi indipendentemente da noi. Questo punto di vista è stato assunto implicitamente da coloro che si occupano della ricerca di intelligenze extraterrestri, i quali mandano nello spazio informazioni sulla scienza umana e sulla matematica sperando di attirare l'attenzione di eventuali extraterrestri progrediti.
Per un realista il numero sette esiste come idea immateriale che possiamo vedere realizzata praticamente in casi specifici come i sette nani, le sette spose e i sette fratelli. Questa concezione è talvolta chiamata platonismo matematico, perché assume l'esistenza di un qualche altro mondo in cui le idee matematiche sono perfette e costituiscono il progetto da cui è derivata la nostra imperfetta conoscenza matematica. Il platonismo, inoltre, assume che il nostro modo di elaborare mentalmente i dati sensoriali non abbia alcun effetto sulla natura matematica della realtà. Questa credenza sembra coincidere con l'idea che Dio sia un matematico, e in effetti se l'intero Universo può essere descritto dalla matematica (come è assunto dalla moderna cosmologia), allora deve esistere una qualche logica immateriale più grande dell'intero Universo materiale.
L'introduzione della interpretazione platonica della matematica dà origine a un impressionante parallelismo tra la matematica e la teologia filosofica. L'intera panoplia delle proprietà e degli attributi di Dio, sviluppata dai primi filosofi religiosi neoplatonici, può essere utilizzata quasi parola per parola per descrivere la matematica, se si sostituisce la parola "Dio" con "matematica". La matematica dei platonisti trascende il mondo ed è considerata come qualcosa che esisteva prima della creazione del mondo reale e che continuerà a esistere anche dopo la sua distruzione. Quando i filosofi antichi tentarono di integrare le leggi della natura in una rappresentazione teologica dell'Universo, vi riuscirono senza grandi difficoltà. Inoltre, riuscirono a incorporare in un modo opportuno anche la sospensione delle leggi della natura, cioè i miracoli. Ma l' onnipotenza di Dio è inadatta alla matematica. Possiamo immaginare una sospensione o una rottura delle leggi della natura (soprattutto perché osserviamo i risultati di tali leggi e non le leggi stesse), ma come la mettiamo con una legge della logica o della matematica? L'opinione teologica medioevale era profondamente divisa sulla possibilità che l' onnipotenza di Dio fosse compatibile con la creazione da parte sua di un mondo in cui esistono impossibilità matematiche. Spinoza credeva in questa libertà, ma contro di lui si schierarono i sostenitori dell'idea che Dio non avesse una tale libertà di manovra, semplicemente perché tale possibilità è inesistente. La questione è se la divinità sia soggetta alle regole della matematica e della logica. La realtà matematica del platonismo contrastava con l'idea di una divinità onnipotente e onnipresente.
Il platonismo giudica l'irragionevole efficacia della matematica nel descrivere la natura come una prova fondamentale a sostegno della propria teoria. Molti scienziati e matematici lavorano giorno dopo giorno come se il realismo fosse vero, anche se poi non se la sentirebbero di difenderlo con troppa decisione durante il week-end.
Ma un realismo di questo tipo ha una conseguenza davvero straordinaria. Se riusciamo a concepire un qualche schema matematico per l'evoluzione dell 'Universo in cui osservatori come noi possono esistere (e chiaramente possiamo farlo) , allora tale scenario deve esistere in ogni senso possibile. Devono necessariamente esistere osservatori intelligenti. Ma, permeato com' è di concetti vaghi, il platonismo non è privo di difficoltà. Dove si trova quest'altro mondo di oggetti matematici che noi scopriamo? Come entriamo in contatto con esso? Se al di là del mondo fenomenico particolare di cui abbiamo esperienza esistono realmente entità matematiche, sembrerebbe allora che l'unica maniera in cui noi possiamo entrare in contatto con esse sia mediante una sorta di esperienza mistica. Tutto questo ha più a che fare con lo spiritismo che con la scienza. Non si può trattare l'acquisizione di conoscenza matematica come si trattano altre forme di conoscenza del mondo fisico. Trattiamo queste ultime come forme significative di conoscenza, perché si riferiscono a oggetti con cui, in un modo o in un altro, possiamo interagire mediante relazioni di causa ed effetto; mentre non c'è alcun modo in cui le entità matematiche possano avere effetto su di noi. Il punto di vista platonico sulla matematica conduce a profondi problemi di natura metafisica. Gödel era un grande sostenitore di questa prospettiva; egli riteneva che esistesse una realtà immateriale con la quale possiamo avere "un altro tipo di rapporto".
Il costruttivismo
Agli inizi del secolo, il costruttivismo fu l'ultima risposta alle incertezze suscitate dai paradossi logici che tempestavano il formalismo. Esso rappresentava la versione matematica della dottrina dell'operazionismo. Il suo punto di partenza, in accordo con Leopold Kronecker, uno dei sui creatori, era la consapevolezza che "Dio creò i numeri interi, tutto il resto è opera dell'uomo". Ciò che egli intendeva dire è che noi dovremmo accettare solo le nozioni matematiche più semplici (l'insieme dei numeri interi 1, 2, 3, 4, 5, ... , il contare) come punto di partenza e quindi derivare ogni altra cosa, passo dopo passo, tramite queste nozioni ovvie e intuitive. Assumendo questo punto di vista conservatore, i costruttivisti volevano evitare di incontrare o manipolare entità come gli insiemi infiniti, di cui non possiamo avere una esperienza concreta e che hanno proprietà non intuitive. Per esempio, un infinito meno un altro infrnito può ancora essere uguale a infinito, come si può vedere sottraendo tutti i numeri pari (un insieme infinito) da tutti i numeri interi (un altro insieme infinito): restano i numeri dispari, cioè un altro insieme infinito. In conseguenza di ciò il costruttivismo è noto anche come intuizionismo, per evidenziare il supposto richiamo all'essenza dell'intuizione umana.
Per i costruttivisti la matematica consiste solamente di quell'insieme di proposizioni che possono essere costruite con un numero finito di passi deduttivi, a partire dai numeri naturali. Il significato di una formula matematica è semplicemente la successione finita di operazioni usata per costruirla. Questa visione può apparire abbastanza innocua, mentre ha importanti conseguenze. Essa crea una nuova categoria di proposizioni matematiche. Ci sono ora tre possibilità per lo status di ogni proposizione: vera, falsa o indecidibile. Se non è possibile stabilire con un numero finito di passi lo status di una proposizione allora essa viene lasciata nel limbo dell'indecidibile. La conseguenza più importante di questa politica è che una proposizione non è più necessariamente o vera o falsa. Questa tricotomia ricorda i tribunali scozzesi, in cui è possibile un verdetto di colpevolezza, non colpevolezza o assoluzione per mancanza di prove (l'ultima sentenza permette di ripetere un processo per la stessa accusa), mentre i tribunali inglesi e americani possono dare soltanto verdetti di colpevolezza o non colpevolezza.
l matematici pre-costruttivisti avevano sviluppato vari metodi per dimostrare la verità delle formule, che non corrispondevano al criterio di un numero finito di passi deduttivi. Un metodo famoso, che risale agli antichi greci, è la reductio ad absurdum. Per mostrare che una proposizione è vera, assumiamo che sia falsa e da questo assunto deduciamo qualcosa di contraddittorio (come 2 = l). Da ciò si conclude che la proposizione originaria è vera. Questo argomento si basa sull'ipotesi che una proposizione possa essere soltanto o vera o falsa. Pertanto esso è considerato non valido dai costruttivisti, secondo i quali una proposizione è vera se, e solo se, può essere dimostrata con un numero finito di passi deduttivi. L'intero corpus dei teoremi della matematica che dimostrano l'esistenza di qualcosa, ma non ne mostrano un esempio esplicito, è fuori gioco.
Se questa filosofia della matematica fosse adottata in fisica, avrebbe conseguenze interessanti e in gran parte inesplorate, poiché molte teorie fisiche, come la teoria della relatività generale di Einstein o la meccanica quantistica di Niels Bohr, usano talvolta degli argomenti non costruttivi o fanno uso del concetto di infinito per dedurre proprietà dell'Universo. Per molti matematici il costruttivismo è alquanto deprimente, come combattere con un braccio legato dietro la schiena. In generale tutti i fisici usano argomenti matematici non costruttivi senza pensarci due volte. L'unica area della fisica in cui le restrizioni imposte dai metodi del costruttivismo e dalla sua logica a tre valori sono state investigate in dettaglio è quella riguardante la misurazione dei quanti. In questo campo le restrizioni costruttiviste sono state proposte come un metodo per risolvere il paradosso di Einstein-Podolsky-Rosen. Ma se questo punto di vista è alla fine quello corretto, esso mina alla radice i nostri tentativi di dedurre una Teoria del Tutto.
C'è sempre stato qualche appassionato difensore dell'interpretazione costruttivista della matematica. Un sostenitore particolarmente dogmatico fu il matematico tedesco Luitzen Brouwer che, nel 1928, quando era redattore del giornale tedesco Mathematische Annalen (la più importante rivista di matematica dell'epoca), dichiarò guerra ai matematici non costruttivisti rifiutando ogni articolo sottoposto per la pubblicazione che usasse metodi non costruttivi, infiniti o la reductio ad absurdum. Ciò creò una certa animosità tra i matematici, in particolare tra Brouwer e Hilbert, che era il direttore degli Annalen. A Hilbert non piaceva Brouwer, che era un individuo catatonico e squilibrato, e si sentiva minacciato dalla popolarità con cui la nuova filosofia costruttivista della matematica prendeva piede.
Hilbert pensava che il costruttivismo avrebbe limitato lo sviluppo della matematica. Cosciente che la sua salute stava peggiorando e temendo per il futuro degli Annalen e della matematica dopo la sua morte, macchinò per rimuovere Brouwer dalla sua posizione di prestigio tra i redattori. Dopo una lunga e dura battaglia, che appariva sempre più ridicola agli estranei (Einstein, un altro membro del comitato di redazione, la chiamò "la grande battaglia della rana e del topo"), Hilbert la spuntò. Il comitato di redazione venne sciolto e ricostituito senza Brouwer. Come risultato, questi si ritirò dal mondo della matematica e dei matematici, per ritornarvi più tardi a propagandare le sue dottrine intuizioniste.
Visto retrospettivamente, il costruttivismo ci appare una dottrina strana: definisce la matematica in un modo antropocentrico come la somma di tutte le dimostrazioni costituite da un numero finito di passi che partono dalla base dell 'intuizione umana: i numeri naturali. La matematica non esiste prima che questo procedimento abbia luogo. A parte la sua ispirazione anti-copernicana, abbiamo già visto come l'idea dell'esistenza di un'intuizione umana universale dei numeri naturali non abbia in realtà un supporto storico. l costruttivisti non potranno mai dire se la mia intuizione è uguale alla vostra, o se l'intuizione umana si è evoluta e si evolverà in futuro. La matematica creata dall'intuizione umana è un fenomeno che dipende dal tempo e dai matematici impegnati nella sua costruzione. La matematica costruttivista è vicina a essere una branca della psicologia. Perché dovremmo cominciare dai numeri naturali? Che cosa costituisce un passo costruttivo? Perché alcune costruzioni sono più utili e meglio applicabili al mondo reale rispetto ad altre? Perché non abbiamo intuizioni degli insiemi infiniti? Come si spiega l'utilità dei concetti non costruttivisti nello studio del mondo fisico? Dopotutto, il concetto di insiemi infiniti è sorto dall'intuizione umana.
La computabilità
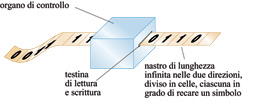
Il costruttivismo, però, ci insegna qualcosa sul carattere matematico della natura. Possiamo vedere come esso contenga residui del programma formalista di Hilbert con le riduzioni dovute alla scoperta di Gödel. Abbiamo imparato che ci sono sempre proposizioni che non possono essere né dimostrate né confutate, ma che ne è di tutte quelle proposizioni la cui veridicità può essere decisa con i metodi tradizionali della matematica? Quante di esse possono essere dimostrate dai costruttivisti? Possiamo costruire, almeno in linea di principio, un computer che riceva un input, mostri lo stato attuale della macchina, sia dotato di un processore che determini un nuovo stato a partire da quello attuale e sia in grado di usare tale sistema per decidere se una certa proposizione è vera o falsa in un tempo finito? Esistono delle caratteristiche specifiche per una macchina in grado di decidere per noi se le proposizioni decidibili della matematica siano vere oppure false? Contrariamente alle aspettative di molti matematici, la risposta è ancora no. Alan Turing a Cambridge, Emil Post e Alonzo Church a Princeton mostrarono che ci sono delle proposizioni la cui veridicità può essere provata solo in un tempo infmito. Esse sono, in effetti, infmitamente più profonde delle dimostrazioni logiche passo dopo passo. Il dispositivo idealizzato che abbiamo descritto è chiamato macchina di Turing (fig. 5) e costituisce l'essenza di ogni moderno computer. Si ritiene che nessun computer reale possegga maggiore abilità nel risolvere problemi.
Le operazioni matematiche che non possono essere calcolate da una macchina di Turing sono dette non computabili. Ne sono noti molti esempi, la cui esistenza genera molti problemi fisici interessanti. Non sappiamo se la natura incorpori cose non computabili nella sua struttura. Se, per esempio, il funzionamento della mente umana o il fenomeno della coscienza umana coinvolgono operazioni non computabili, allora le ricerche sull'intelligenza artificiale non possono riuscire a produrre un computer in grado di imitare completamente la complessità della coscienza umana. Se tale restrizione sia di un qualche interesse pratico dipende da quanto sono importanti gli aspetti non computabili per il funzionamento del cervello. Al momento sembra non essere così, ma la nostra comprensione del funzionamento del cervello è ancora così incompleta che il dibattito deve essere considerato aperto.
Tornando al rompicapo dell'applicabilità della matematica alla natura, possiamo riformularlo come un'interessante proposizione sulla computabilità. Se una operazione è computabile, significa che possiamo costruire materialmente un dispositivo il cui comportamento simuli quell' operazione matematica. Esempi di tali dispositivi sono il pendolo, i decadimenti radioattivi e gli impulsi elettrici. D'altro canto, dispositivi come questi possono essere ben descritti da operazioni matematiche computabili. Che la natura sia ben descrivibile dalla matematica è come dire che le più semplici operazioni matematiche, come l'addizione e la moltiplicazione, e le operazioni più complesse usate così efficacemente in campo scientifico, sono funzioni computabili. Se così non fosse, allora non potrebbero essere equivalenti ad alcun processo naturale e noi non saremmo così tanto impressionati dall'utilità pratica della matematica. Anche se questi fenomeni avessero un carattere matematico, la matematica non si rivelerebbe un linguaggio straordinariamente utile nel descrivere e nel prevedere il funzionamento della natura.
Una domanda interessante è se le leggi di natura contengano elementi non computabili. Coloro che hanno tentato di creare una teoria quantistica dell'intero Universo hanno già affrontato questa possibilità. Esistono attributi dell'Universo potenzialmente osservabili, definiti da somme infinite di termini, la cui completa catalogazione non è computabile. Essi non possono essere catalogati con alcun calcolo sistematico che si limiti ad applicare ripetutamente gli stessi principi. Ciascun elemento richiede principi differenti e qualitativamente nuovi.
Abbiamo fatto una distinzione tra operazioni computabili e operazioni non computabili. Ma nella vita reale computabile non coincide con utile se il programma in grado di fare il calcolo richiede milioni di anni per essere eseguito. Il mondo potrebbe essere matematico, e addirittura possedere funzioni computabili in abbondanza, ma queste potrebbero essere di una profondità e complessità tali che non saremmo in grado di trovare algoritrni che richiedano meno di migliaia di anni per essere eseguiti sul più veloce computer esistente. In effetti, l'esistenza di tali difficili problemi è molto sfruttata nel mondo moderno. Molti codici sofisticati usati per motivi di segretezza militare o commerciale sono basati su algoritmi che in linea di principio possono essere scoperti, ma in pratica sono sicuri. In altre parole, il computer più veloce impiegherebbe migliaia di anni per cercare tutte le combinazioni necessarie a scoprire il codice (e per quel tempo, ovviamente, il codice sarebbe stato cambiato).
Codici come questi si basano sull' esistenza di operazioni matematiche chiamate funzioni trappola che possono essere calcolate facilmente in una direzione, ma sono praticamente impossibili da invertire, proprio come è facile cadere in una trappola, ma non è facile uscirne arrampicandosi. Per esempio, prendiamo due numeri primi molto grandi, ciascuno contenente centinaia di cifre, e moltiplichiamoli; questa è una operazione che un computer può fare in una frazione di secondo. Ma se si dà a un qualunque computer il risultato di una tale operazione e si chiede di trovare i due numeri primi che lo dividono, ci potrebbe volere una vita prima di avere la risposta. La lezione che questo esempio ci dà è che la natura potrebbe essere codificata in un qualche modo matematico e la codificazione potrebbe forse corrispondere a una qualche sua legge; noi potremmo scoprire tale codice usando magari soltanto pochi principi di simmetria, coerenza e semplicità, ma non saremmo comunque in grado di invertire l'operazione e determinare la vera natura delle cose dal loro aspetto codificato.
lllustriamo con un semplice esempio il modo in cui le funzioni trappola vengono usate per la codificazione. Supponiamo che io voglia mandarvi un messaggio segreto. Il mio 'codice' è alquanto primitivo e consiste nel mettere il messaggio in una scatola di metallo e chiuderla con un lucchetto. 'Decodificare' significa aprire il lucchetto. Come posso mandarvi il messaggio senza mandarvi anche la chiave, e così correre il rischio che venga in possesso di qualcuno che vorrebbe rubarlo? Sembra una cosa impossibile, ma non lo è. Il sistema funziona così: io chiudo la scatola con il lucchetto, poi ve la spedisco e conservo la chiave. Voi attaccate un altro lucchetto alla scatola e lo chiudete a chiave, poi mi rimandate la scatola. lo rimuovo il mio lucchetto e vi mando di nuovo indietro la scatola. Quando la ricevete per la seconda volta rimuovete il vostro lucchetto e potete prendere il messaggio. Così nessuno di noi ha bisogno di sapere niente circa la chiave dell'altro! Nella vita reale si usano i numeri primi invece delle chiavi. Questa idea così semplice e brillante è nota soltanto da meno di venti anni. Recentemente sono stati proposti metodi che permetterebbero di infrangere questi codici. La tecnica non è un metodo per fattorizzare numeri grandi in numeri primi. Pare che bombardando con radiazioni il messaggio codificato si producano degli errori nel processo; esaminando lo stesso messaggio più volte dopo aver introdotto una sequenza di piccoli errori in questo modo, sembra che il codice possa essere scoperto e il messaggio letto.
I paradigmi
Le nostre categorie di pensiero sono spesso influenzate da certe tendenze culturali. Le nostre rappresentazioni dell'Universo tendono a fare uso di concetti alla moda che si sono dimostrati utili in circostanze più terrene. Così, nei tempi antichi troviamo rappresentazioni dell'Universo come un organismo o come espressione di un'armonia statica e geometrica. Per Newton, e per gli utilizzatori dell'orologio a pendolo appena inventato, l'Universo appariva regolato ritmicamente. Per i vittoriani della rivoluzione industriale il paradigma dominante era la macchina o il motore a vapore. Oggi sono il computer e i microchip a governare la nostra vita quotidiana. Sarebbe troppo aspettarsi che tale paradigma possa essere ignorato nel nostro tentativo di comprendere l'Universo.
Con un pizzico di buon senso kuhniano, potremmo prendere questa immagine come l'ultima di una sequenza senza fine di idee alla moda, che saranno abbandonate all'avvento della prossima rivoluzione tecnologica. Consapevoli di questa possibilità, supponiamo non di meno che il calcolo abbia un significato non effimero. Possiamo chiederci se sia più fondamentale pensare alla struttura e all'evoluzione dell'Universo come a un calcolo o come a una conseguenza di leggi della natura. 0, mettendo insieme i due concetti, se sia il caso di trattare le leggi della natura come se fossero un tipo di software che viene eseguito dal contenuto materiale del nostro Universo. Mentre l'immagine delle leggi di natura come simmetrie e invarianze, tanto amate dai fisici, si accordano naturalmente con la visione platonica della realtà, l'immagine computazionale sembra essere più vicina alla più limitata visione costruttivista.
La compressione dell'informazione nei numeri e nella natura
La conseguenza più fruttuosa di un'immagine computazionaIe della natura è che essa rivela perché la natura ci appaia comprensibile, perché la scienza sia possibile, e chiarisce perché la matematica sia così efficace nella descrizione del mondo fisico. Se ci viene presentata una sequenza di numeri o simboli, possiamo sostituirla con una proposizione abbreviata che possiede lo stesso contenuto d'informazione. Quindi la sequenza infmita di numeri 2, 4, 6, 8, 10, 12, 14, ... potrebbe essere sostituita da una formula per generare i numeri pari. Se una sequenza può essere sostituita da un programma in grado di generarla, che sia più corto della sequenza stessa, allora diciamo che la sequenza è algoritmicamente comprimibile. Se una sequenza non può essere sintetizzata in alcun programma o regola generatrice più corti della sequenza stessa, allora diciamo che essa è casuale. Le sequenze realmente casuali non possono essere compresse in formule semplificatrici. Esse sono algoritmicamente incomprimibili. Questa distinzione tra casualità e ordine ricorda il modo in cui la nostra mente reagisce quando ci viene mostrata una stringa di numeri. Noi cerchiamo una regola o un modello in grado di generare la sequenza.
Una sequenza è casuale se la sua complessità uguaglia la lunghezza della sequenza stessa. In questo caso è necessaria l'intera lista per specificare il suo contenuto d'informazione. Perciò, date due sequenze casuali qualunque di lunghezza differente, quella più lunga viene considerata la più complessa. Se prendiamo un gran numero di sequenze di numeri, per esempio numeri di telefono, si troverà che molte possiedono una elevata complessità ed è piuttosto raro imbattersi in stringhe con bassa complessità. Usando tale nozione di complessità, immaginiamo di dare a un computer, che conosca tutti i simboli e le operazioni dell' aritmetica, la seguente istruzione:
"Scrivi una sequenza la cui complessità sia superiore a quella di questo programma".
Il computer non può rispondere. Le sequenze che può generare devono per definizione avere una complessità minore del programma stesso. Siamo ora in grado di sfruttare questa imbarazzante situazione per mostrare che devono esistere proposizioni indecidibili. Prendiamo semplicemente una sequenza a caso, chiamiamola R, la cui complessità è superiore a quella del sistema del computer. Una domanda come
"R è una sequenza casuale?"
è indecidibile per il computer. La complessità delle proposizioni "R è casuale" e "R non è casuale" è troppo grande per essere tradotta dal sistema operativo del computer. Esse non possono essere né provate né confutate. Il teorema di Gödel è così dimostrato.
Fino a poco tempo fa la successione di scoperte iniziata da Gödel sembrava essersi arrestata. Il pozzo dell'indecidibilità sembrava essersi prosciugato lasciando la sua grande scoperta a brillare come un monumento mentre il corso della matematica si era spostato da qualche altra parte. Poi, verso la fine degli anni Ottanta, fu scoperta questa nuova e più semplice via di dimostrare i teoremi di Gödel, riformulandoli in proposizioni sull'informazione e la casualità. Possiamo associare una certa quantità di informazione agli assiomi e alle regole di ragionamento che defmiscono un certo sistema assiomatico e possiamo definire il suo contenuto di informazione come la dimensione di un programma per computer in grado di cercare tutte le possibili catene di deduzioni e dimostrare tutti i possibili teoremi. Questo approccio porta alla conclusione che nessun numero la cui complessità sia maggiore di quella del sistema assiomatico può essere dimostrato essere casuale. Anche volendo superare questa mancanza aggiungendo assiomi o regole di inferenza per aumentare il contenuto di informazione del sistema, esisteranno sempre numeri più grandi la cui casualità non può essere dimostrata. C'è un limite reale al potere della matematica. In particolare, il matematico americano Gregory Chaitin ha esplorato le conseguenze di questa linea di pensiero nel contesto di un famoso problema di matematica. Se scriviamo una equazione che connette due (o più) quantità X e Y nella forma X + y2= l e se non ci limitiamo ai numeri interi, allora esistono un'infinità di coppie (X, Y) che risolvono l'equazione (per esempio X = 3/4, Y = 1/2). Ma supponiamo di essere interessati solo alle soluzioni costituite da coppie di numeri interi positivi. Questo è chiamato problema di Diofanto in onore di Diofanto di Alessandria (fig. 6), il più grande algebrista dell'antichità, che fu il primo a fare un uso sistematico dei simboli algebrici, usando simboli speciali per le quantità incognite, i reciproci e le potenze dei numeri, e che risolse molte equazioni di questo tipo. Questi problemi hanno più di una soluzione possibile. Nel nostro esempio elementare di equazione diofantea, X + y2 = l, le sole soluzioni intere sono le coppie (X, Y) = (1,0) e (0,1). Possiamo creare un'altra equazione diofantea contenente la variabile A, che può prendere qualunque valore intero positivo 1, 2, 3, 4, .. e così via. Per esempio,
X + y2 =A
si riduce all'esempio precedente nel caso A = 1. Supponiamo di creare una equazione diofantea più elaborata che contiene N diverse variabili Xl, X₂, X₃, ",XN a primo membro, al posto di sole due (X e Y), e la costante intera A. Chaitin si è chiesto se, per ciascun valore di A = 1, 2, 3 ... e così via, un'equazione di questo tipo abbia un numero finito o infinito di soluzioni tra i numeri interi. A prima vista questo appare poco diverso dal problema di quante siano le soluzioni intere per ciascun valore di A. Ma rispondere a questo quesito è infinitamente più difficile. Sembra che non ci sia modo di determinare la risposta. La risposta è casuale, nel senso che per trovarla è necessaria più informazione di quanta ne contenga l'aritmetica. Essa non può essere calcolata riducendola ad altri fatti o assiomi matematici. Chaitin ha rappresentato questo stato di cose formando un numero Ω le cui cifre sono una sequenza di numeri binari 0 e 1 scelti nel seguente modo: si prenda ciascun valore di A e si scriva, per ogni A-esima cifra di Ω, 0 se l'equazione diofantea con A ha un numero finito di soluzioni e 1 se ne ha un numero infinito. Il risultato è una successione binaria di 1 e 0, per esempio,
Ω = 0010010101001011010 ..
(e così fino all'infinito), che specifica un numero reale. Chaitin ha dimostrato che Ω è un'autentica 'nuvola di ignoto': il suo valore non può essere calcolato da alcun computer; nessun programma per computer, non importa quanto complesso, può mai far meglio che calcolare una parte finita del numero infinito di cifre necessarie a specificare Ω. Questa limitazione nasce dal fatto che ciascuna cifra di Ω viene prodotta in modo logicamente indipendente dalle altre. Non esiste una formula che permetta di generare la cifra successiva all'ultima ottenuta. Nessuna macchina che segua semplicemente una data regola o programma possiede quell'ingrediente di novità che è necessario per trovare l'elemento successivo nella lista. Alla fine Chaitin riscrisse questo numero mettendo una virgola decimale di fronte a esso, così
Ω =0,0010010101001011010 ...
Tale numero dà la probabilità che un programma per computer scelto a caso, con un input casuale, si fermi dopo un numero finito di passi. Il suo valore è sempre un numero compreso tra (ma non uguale a) zero e uno. Se fosse zero significherebbe che tutti i programmi si fermano, mentre l'altro estremo, uno, significherebbe che nessun programma si ferma. Questo fatto ha l'ulteriore importante conseguenza che, se prendiamo un valore di A dell' equazione diofantea pari a un numero intero molto grande, non c'è modo di decidere se la A-esima cifra di Ω sia uno zero o un uno. Inoltre, questa situazione si presenta per un numero infinito di scelte possibili di A. Il ragionamento umano non potrà mai rispondere a questa domanda. Si tratta di una domanda la cui risposta non corrisponde a un teorema in alcun sistema formale. Anche l'aritmetica contiene la casualità. Alcune delle sue verità possono essere stabilite solo con il metodo sperimentale. Vista in questo modo, la matematica comincia ad assomigliare a una scienza sperimentale. L'inevitabile indecidibilità di certe proposizioni mostrate da questo esempio nasce perché il sistema logico di un computer, basato sull'aritmetica, possiede una complessità troppo piccola per coprire lo spettro di tutte le proposizioni che possono essere composte usando il suo alfabeto. Come conseguenza, non c'è modo per decidere se il programma che stiamo usando per un particolare scopo sia il più corto possibile. La relazione generale tra i nostri numeri necessaria ad abbreviare il programma potrebbe essere una verità indecidibile dell' aritmetica. Risultati come questo pongono delle restrizioni alle finalità di qualunque approccio alle leggi di natura basato solo sulla semplicità. L'analogo scientifico della metodologia formalista in matematica è l'idea che, data una qualunque sequenza di osservazioni della natura, si cerchi di descriverle tramite una legge matematica che le includa tutte. Ci può essere ogni sorta di legge a generare quella sequenza di dati, ma alcune saranno macchinose e innaturali. Gli scienziati preferiscono scegliere leggi che abbiano complessità minima, nel senso descritto precedentemente, che codifichino cioè l'informazione in un algoritmo nel modo più sintetico. Alcune volte questo pregiudizio è chiamato rasoio di Occam. È evidente come questo approccio non ci permetterà mai di dire se una legge che abbiamo formulato costituisca una descrizione completa della natura. Esisteranno sempre proposizioni indecidibili che possono essere formulate nel suo linguaggio, e quindi non si potrà mai dimostrare quale sia la più semplice codifica dei fatti. Sfortunatamente, non si potrà mai sapere se si è scoperto il segreto dell 'Universo e se ciò che resta da spiegare sia banale o sia un'impresa enorme.
La scienza esiste perché il mondo naturale sembra essere algoritmicamente comprimibile. Le formule matematiche che chiamiamo leggi di natura sono compressioni sintetiche di lunghe sequenze di dati sull'evoluzione del mondo. Questo è ciò che intendiamo quando diciamo che il mondo è intelligibile. Possiamo concepire un mondo in cui tutti i fenomeni siano caotici (esattamente come certi ci appaiono). Le sue proprietà potrebbero essere descritte soltanto elencando le innumerevoli sequenze dei dati osservati. La scienza diventerebbe molto più simile al train-spotting (bizzarro passatempo britannico, oggi inusuale, che consiste nel prendere nota dei numeri di serie dei treni che passano, numeri ovviamente senza alcuna correlazione tra loro). l fenomeni osservati avrebbero quell'unicità che troviamo nel mondo dell' arte creativa. Se l'Universo è unico e necessario, allora non dovremmo stupirci di trovarlo, nel complesso, come una entità algoritmicamente incomprimibile e in ultima analisi non riducibile ad alcuna formula, definito da niente altro che dalla sua completa e incatalogabile sequenza di eventi.
Sappiamo che il mondo presenta particolari processi caotici che non sono algoritmicamente comprimibili, esattamente come esistono operazioni matematiche che sono calcolabili. È questo bagliore di casualità che ci fa intravedere come apparirebbe un mondo completamente incomprimibile. Gli scienziati sarebbero bibliotecari invece che matematici, che catalogano fatti dopo fatti, senza collegamento, e il problema dei fatti, come qualcuno ha fatto notare, è che ce ne sono tanti.
Vediamo la scienza come la ricerca di una compressione algoritmica del mondo delle esperienze, e la ricerca di una singola Teoria del Tutto che comprenda ogni cosa come ultima espressione della profonda fiducia di alcuni scienziati che la struttura dell 'Universo, nella sua essenza, possa essere algoritmicamente compressa. Quelle che chiamiamo leggi di natura potrebbero essere la parte più sbalorditivamente comprimibile. Riconosciamo però che la mente umana gioca un ruolo non banale in questa valutazione. Infatti, l'abilità della mente umana a fare compressioni è inestricabilmente legata alla apparente comprimibilità algoritmica del mondo. La nostra mente si è sviluppata grazie agli elementi del mondo fisico e si è perfezionata, almeno parzialmente, verso il suo stato attuale in un processo perpetuo di selezione naturale. La sua efficacia nel prendere coscienza dell'ambiente, la sua capacità di sopravvivenza, sono ovviamente correlate con la sua capacità di compressore algoritmico. Più un organismo è efficiente nel memorizzare e codificare le esperienze nel mondo fisico, più efficientemente tale organismo sarà in grado di reagire ai pericoli che un ambiente altrimenti imprevedibile presenta.
Questa abilità ha raggiunto nuovi livelli di sofisticazione nella nostra più recente fase di storia come Homo sapiens. Siamo in grado di pensare sul pensiero stesso. Invece di imparare dall'esperienza come parte di un processo evolutivo, abbiamo sufficiente capacità mentale per immaginare e simulare i probabili risultati delle nostre azioni e integrare l'esperienza passata nelle nuove situazioni. È evidente che, per raggiungere una efficace compressione algoritmica, questa capacità mentale deve essere superiore a un certo livello. I nostri sensi devono essere ricevitori abbastanza sensibili da garantire una quantità significativa di informazioni dall'ambiente. Ma c'è un limite anche a questo. Se i nostri sensi fossero così sviluppati da poterci trasmettere ogni informazione possibile sulle cose che osserviamo o sentiamo (tutti i più piccoli movimenti atomici) allora la nostra mente sarebbe sovraccarica di informazioni. L'elaborazione sarebbe lenta, i tempi di reazione lunghi, e sarebbe necessaria ogni sorta di circuiti addizionali per filtrare rappresentazioni dell'informazione a livelli differenti di intensità e profondità.
Ci sarebbe un prezzo evolutivo da pagare per l'uso di tutte queste risorse necessarie per elaborare tanta informazione, molta della quale porterebbe un beneficio relativamente piccolo. È meglio investire nella capacità di correre più veloci o in quella di digerire differenti tipi di cibo. Il fatto che la nostra mente non ambisca troppo di procurarsi le informazioni e di sviluppare la sua capacità di elaborarle significa che il cervello effettuerebbe una compressione algoritmica dell'Universo, che questo sia o no intrinsecamente comprimibile. In pratica il cervello procede per approssimazioni, trascurando alcuni dei dati che gli sono disponibili, a causa della limitata sensibilità. Spesso questo processo di approssimazione viene alquanto formalizzato, diventando esso stesso una branca della scienza applicata. Un buon esempio è la statistica. Quando studiamo fenomeni molto grandi e complicati possiamo provare a comprimere le informazioni disponibili prendendo campioni con qualche criterio selettivo. Per esempio, nelle anticipazioni elettorali si cerca di prevedere il comportamento dell'opinione pubblica prima di una elezione generale, senza realmente chiedere a tutti i cittadini di uno stato per chi realmente voteranno. In pratica lo si chiede a un sottoinsieme rappresentativo della popolazione e ciò usualmente produce una previsione incredibilmente buona del risultato dell'elezione vera.
La matematica è utile nella descrizione del mondo fisico perché il mondo è algoritmicamente comprimibile. Essa è il linguaggio dell'abbreviazione delle sequenze. La mente umana ci permette di pensare e memorizzare. I limiti che la natura impone ai nostri organi sensori ci proteggono da un eccesso di informazioni sul mondo. Questi limiti agiscono come valvole di sicurezza per la mente. Tuttavia dobbiamo tutto alla straordinaria capacità del cervello di sfruttare la comprimibilità algoritmica del mondo.
L'inevitabilità della matematica
La matematica può essere vista come l'insieme di tutte le possibili forme di interrelazioni. Molti dei suoi concetti, come le funzioni, le trasformazioni, i programmi, i calcoli, sono descrizioni di relazioni tra uno stato e un altro. Mentre nel mondo antico si credeva nella numerologia, la quale attribuiva un significato ai singoli numeri (i numeri fortunati giocano ancora un ruolo importante nel pensiero umano), la matematica moderna vede un significato solo nelle relazioni tra i numeri. Se la matematica è catalogazione di tutte le possibili forme, alcune concrete, altre astratte, allora l'esistenza della matematica è inevitabile, così come il suo ruolo centrale nella comprensione dell'Universo. Se l'Universo esiste per contenere la complessità, e quindi osservatori coscienti di ogni tipo, allora esso non può essere un caos senza alcuna forma. Esso deve contenere esempi di un qualche tipo di forma affrnché forme di complessità organizzata possano esistere e l'evoluzione per selezione naturale possa avere luogo. Perciò la forma, e quindi la matematica, che è la descrizione di quella forma, è inevitabile. Noi non potremmo esistere in un mondo dove la matematica non fosse presente. Ma questo non risolve il mistero di perché troviamo la matematica così utile. Sarebbe stato possibile che il mondo avesse una forma tale da essere dominato da funzioni non computabili, e noi non avremmo trovato la matematica utile in pratica. Il mistero del nostro Universo è che esso è estremamente comprimibile e che un piccolo numero di semplici funzioni computabili è in grado di descrivere quasi tutto quello che abbiamo incontrato nell'Universo fisico.
Bibliografia generale
BARROW, J.D. The world within the world. Oxford, Oxford University Press, 1988.
BARROW, J.D. Pi in the sky: counting, thinking and being. Oxford, Clarendon Press e New York, Oxford University Press, 1992.
BENACERRAF, P., PUTNAM, H., a c. di Philosophy of mathematics: selected readings. 2a ed. Cambridge, Cambridge University Press, 1983.
CHAITIN, G. (1988) Randonmess in Aritlnnetic. Scient. Am., 259, 80-85.
DAVIS, P.I., HERSH, R. The mathematical experience. Boston, Birkhäuser, 1981.
FANG, l Bourbaki. New York, Paideia Press, 1970.
HERKEN, R., a c. di The universal Turing machine: a halfcentury survey. Oxford, Oxford University Press, 1988.
GEROCH, R., HARTLE, J. Computability and physical theories. In Between quantum and cosmos: studies and essays in honor of John Archibald Wheeler, a c. di Zurek W., Van der Merwe A., Miller W.A., Princeton, Princeton University Press, 1988, pp. 549-567.
MADDY, P. Realism in mathematics. Oxford, Clarendon Press e New York, Oxford University Press, 1990.
PENROSE, R. (1990) Précis ofthe Emperor's new mind: concerning computers, minds, and the laws of physics (together with responses by critics and an extended reply by the author). Behavioural and Brain Sciences, 13, 643-705, 1990.
RUCKER, R. Infinity and the mind: the science and philosophy of the infinite. Boston, Birkhäuser, 1982.
SHANKER, S.G. Gödel's theorem in focus. Londra-New York, Croom Helm, 1988.
VAN STIGT, W.P. Brouwer's intuitionism. Amsterdam, Elsevier, 1990.
TYMOCZKO, T., a c. di New directions in the philosophy ofmathematics: an anthology. Boston, Birkhäuser, 1986.
WIGNER, E. (1960) The unreasonable effectiveness of mathematics in the natural sciences. Commun. Pure Appl. Math., 13, 1.